International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Comparative Analysis of GA-MMSE and PSO-MMSE Based MUD Technique Aided SDMA/OFDM System

Medha Vijayvargiya1, Manish Kumar Gurjar2
  1. MTech Student [Digital Comm.], Dept. of ECE, TIT College, Bhopal, India1
  2. Assistant professor, Dept. of ECE, TIT College, Bhopal, India2
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Smart antenna primarily uses the SDMA-OFDM based architecture of communication. Due to robustness and protection against interference provide by OFDM (Orthogonal Frequency division multiplexing). Although High data rate transmission is effectively achieved by using OFDM but detection techniques especially in over-loaded scenario poses many challenging issues. There are many optimization techniques presents for optimal multiuser detection process in SDMA-OFDM system, though each method is suffered from limitations. In these paper two popular evolutionary algorithms such as particle swarm optimization (PSO) hybrid with MMSE technique and genetic algorithm (GA) based SDMA-OFDM multi user detection (MUD) is hybrid with the MMSE technique. These optimization multiuser detection (MUD) techniques are simulated using three different modulation techniques these are PSK, QAM and its performance is compared against four existing MUDs such as MMSE(Minimum mean square) GA(Genetic Algorithm),PSO and ZF(Zero forcing) varying different parameters. Concatenated PSO-MMSE and GA-MMSE, the two methods are better in terms of simulation and reduces complexity. These techniques are proved to provide a very high performance when comparing with the existing detectors especially in a rank-deficient scenario in which numbers of users are very high as compare to transmitting antenna. From the experimental results it is crystal clear that GA-MMSE and PSO-MMSE improve the results by 29.8% than existing multiuser detection technique and BER reached to a level of 0.01.

Keywords
OFDM, SDMA, Multiuser Detection (MUD), Genetic Algorithm (GA).

INTRODUCTION
Orthogonal Frequency Division Multiplexing (OFDM), is the basic unit of all multicarrier communication systems, receives wide interest especially for high data-rate transmission because of its robustness in frequency selective fading channel. The employment of multiple antennas at both the transmitter and the receiver, which is hugely referred as MIMO technique, contains a cost-effective technique to high-throughput wireless communication [1 2]. OFDM is also referred as a method of encoding digital data on multiple carrier frequencies. OFDM has transformed into a famous scheme for wideband digital communication, wireless or over copper wires, used in applications for example audio television and digital broadcast, DSL Internet access, wireless networks, power line networks and 4G mobile communications. SDMA based techniques as a subclass of MIMO systems, is one of the most promising techniques for solving the limitation of wireless communication systems. SDMA enables multiple users to simultaneously share the same bandwidth in different geographical locations. The exploitation of the spatial dimension makes it enable to identify the individual users, even when these users are in the same code or time or frequency domains, thus increasing the system’s capacity [1, 4]. Detection techniques especially in over-loaded situation pose many challenging issues. The higher the number of users to be supported, the more challenging the optimization task becomes, due to the exponentially increased number of dimensions to be estimated. There are many conventional multiuser detection techniques like Minimum mean square error, Zero forcing. And there is two evolutionary optimization techniques are there namely genetic algorithm and particle swam optimization techniques. The family of GAs can be efficiently incorporated into SDMA-OFDM systems and thus solve many challenging issues. In literature, GA based technique with better convergence properties and lower computational complexities are discussed in detail. Possibility of applying optimization techniques other than GA led to the implementation of latest and robust stochastic PSO algorithm. These detection techniques also suffer from specific limitations in rank-deficient scenario [1] Hence the MMSE-SDMA-OFDM system BER performance may be potentially further improved with the aid of hybrid GAMMSE and PSO-MMSE which is capable of exploiting the output provided by the MMSE MUD in its initial population. In this paper we have compare the BER obtained by different multiuser detection technique using 3 different modulation techniques such as PSK and QAM. The SDMAOFDM system is simulated using MATLAB Software. And the results of these techniques are compare to evaluate the best optimization techniques which is having minimum BER.
The structure of this paper is as follows. Section II Mathematical definition of OFDM and the model of SDMA-OFDM, system model.Section III various MUD techniques. Simulation results and analysis are presented in Section IV. While final Conclusion is offered in Section V.

MATHEMATICAL DEFINATION OF OFDM
OFDM consists of multiple carriers. Each carrier can be presented as a complex waveform like:
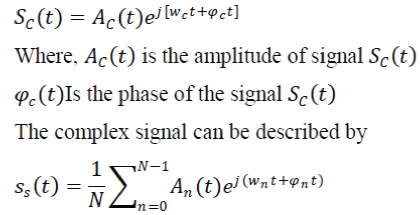image
This is a continuous signal. Each component of the signal over one symbol period can take fixed values of the variables like:
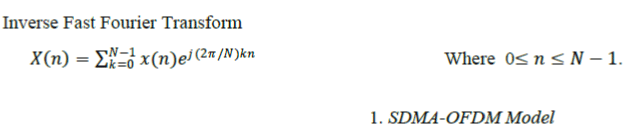image
image

SDMA-OFDM Model
In SDMA-OFDM systems, the L transmitted signals of users each equipped with a single transmitting antenna and received by the P number of receiving antennas of the BS as shown in Figure. At the BS, the received signal was corrupted by the Additive white Gaussian noise or at the antenna array elements yielding
image

MULTIUSER DETECTION TECHNIQUES
We are discussing below some multiuser detection techniques for performance investigation:
A. Zero Forcing (ZF)
B. Minimum Mean Square Error(MMSE)
C. GA(genetic algorithm)
D. PSO(Particle swarm optimization)
E. Concatenated GA-MMSE and PSO-MMSE

A. Zero Forcing
The problem in MMSE section here can be overcome by using the matrix w which should satisfy WH=I condition. The Zero Forcing (ZF) detector for getting this constraint is given by
image
This matrix is also called as the pseudo inverse m x n matrix.
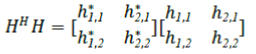image

B.MMSE
MMSE detection is also a linear but it assumes a prior knowledge of noise variance and channel covariance. Due to this it is a more accurate detection scheme compared to ZFMUD. This algorithm detects user as
image
Where σ^2 is the variance of i.i.d. complex Gaussian random noise with zero mean H indicates Hermitian.

C. Genetic Algorithm
GA assisted MUD techniques is basically an optimization and search technique that mimics elements seen in natural evolution and it could be used in computation to get approximate or exact solutions to both optimization and as well as search problems. In order to restrict the search space, GA implement search mechanisms aims to find a solution based on an objective function (or fitness value)[1]. An important step to apply the GA is to define the objective function that is unique for each optimal problem this is the Decision metric required for the receive antenna, namely the antenna specific objective function is define as:
image
Where yp is the received symbol at the output of the pth receiver, while Hp can be represented as the pth row of the H channel transfer function. Thus, the estimated transmitted symbol vector of the received signal at the pth receiving antenna is given by:
image
The main steps of GA implemented in SDMA-OFDM [1] as shown in Fig. 1 are described below:
Step 1: Define the objective function, and then set the parameters of GA including the probability and type of mutation and crossover operations, maximum number of generations, population size, and the termination criteria.
Step 2: Evaluate the fitness for each individual in the population, where the fit individual in our MUD minimization problem will have the lowest numerical value. The first/initial generation is produced.
Step 3: Test the termination criteria like reaching the maximum number of generations or getting the minimum tolerance error between the received signal y and the multiplication between channel matrix H and transmitted signal x.
If the termination criteria not met with the previous population than genetic algorithm will be applied as following:
A. Individual are chosen according to their fitness for the reproduction of offspring.
B. Binary representation is used in this work with double point crossover.
C. All offspring will be mutated with a certain probability .By mutation individuals are randomly altered.
Evaluated in step 2.this cycle is performed continuously until the optimizations criteria are attained.
Step 4: If the individual generated will met the termination criteria, the decision will be taken. These individual or gene is chosen as the best gene and finish algorithm.

D. PARTICLE SWARM OPTIMIZATION
In PSO we take a initial population ,the particles of this population are placed in search space of some function or problem and each evaluate the o objective function at its present locations. Now each particle then follow the movement through the search by combining some part of the history of its own preset and best locations with those of one or more member of the swarm with some random perturbations. The next iteration takes places when all particles have been placed[4]. Eventually the swarm as a whole like a flock of birds collectively searching for food will start moving closer to optimum of the fitness function Algorithm.
 Initialize a population array of particle with random position and velocity.
 Calculate the fitness value of each particle.
 Compare the particle fitness evaluation with its pbest.
 If current value is better than set pbest apbest equal to current value. And if not than keep the pbest value.
 Assign the best value to the gbest.
 Now calculate the velocity for each particle.
 Use each particle velocity value to update its data value. Now compare with the target.
 Now compare this with target.if target reached then terminate the process.

E. CONCATENATED GA-MMSE AND PSO-MMSE
The BER performance of the MMSE MUD is somewhat limited, since it is the total mean-square estimation error imposed by the different simultaneous users that is minimized, rather than directly optimizing the BER performance. Therefore, the MMSE-SDMA-OFDM system’s BER performance may be potentially further improved with the aid of hybrid GA aided MUD, which is capable of exploiting the output provided by the MMSE MUD in its initial population.
In uplink SDMA-OFDM systems, at the kth subcarrier of the nth OFDM symbol we have obtained the complex signal vector x [n, k] by the P-element receiver antenna array have, which is the superposition of the faded signals associated with the L mobile users and contaminated by the Additive White Gaussian Noise (AWGN), expressed as:
X[n, k]=H[n, k]S[n, k]+ N[n, k]
As shown in the upper half of Figure 3.Iinformation bit blocks b(l) l , ··· ,L of the L mobile users are first encoded by the L independent FEC encoders. The resultant coded bits b(l)s are then mapped to Pulse Amplitude Modulation, Quadrature Amplitude Modulation (QAM) or Phase-Shift Keying (PSK). Symbols s(l), which are modulated by the Inverse Fast Fourier Transform (IFFT) and then forwarded to the SDMA MIMO channel model. At the Base Station shown at the lower half of Figure, the received signal is the noise-contaminated superposition transmitted signals is OFDM-demodulated at the P receiver antenna elements and forwarded to the iterative GA- MMSE and PSO-MMSE MUD[1,6]. Then the detected soft bitsˆ b(l) s are generated, which are forwarded to the L independent FEC decoders for channel decoding.

SIMULATION OF MUD TECHNIQUES
SDMA-OFDM system is implemented under MATLAB environment. Here we have taken two modulation techquies like PSK and QAM for comparing the optimization technique for multiuser detection.

CONCLUSION
In this paper we have compared the different method of multiuser detection technique like ZF, MMSE, GA, PSO with concatenated techniques like GA-MMSE and PSO-MMSE technique in SDMA-OFDM system. The two different modulation techniques are used for the comparative analysis namely PSK and QAM. From the simulation conducted it has been concluded that in PSK modulation the hybrid technique GA-MMSE and PSO-MMSE has BER of 0.09 db. In QAM the value is 0.01 db which is excellent result so far. It has been shown that concatenated technique i.e. GAMMSE and PSO-MMSE design is capable of achieving better performance and hence of improving the system capacity, compare to MMSE, ZF, GA and PSO mud techniques in SDMA/OFDM system.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 5 Figure 6 Figure 7
Figure 5 Figure 6 Figure 7
 

References
  1. jorge magalhães “A Comparative Study of Crossover Operators for Genetic Algorithms to Solve the Job Shop Scheduling Problem” WSEAS TRANSACTIONS on computers Issue 4, Volume 12, April 2013.K. Elissa.
  2. M. A. Alansi, I. M. Elshafiey “Genetic Algorithm Optimization Tool for Multi-user Detection of SDMA-OFDM Systems”. PIERS Proceedings, Kuala Lumpur, MALAYSIA, March 27-30, 2012
  3. Susmita Das and Kala Praveen Bagadi “Comparative Analysis of Various Multiuser Detection Techniques in SDMA-OFDM SystemOver the Correlated MIMO Channel Model forIEEE 802.16n”,world acadmey of science,engineering and technology 53, 2011.
  4. Chen, S., T. R. Newman, J. B. Evans, and A. M. Wyglinski, \Genetic algorithm-based optimization for cognitive radio networks," Sarnoff'10 Proceedings of the 33rd IEEE Conference Sarnoff, 2010.
  5. M. Jiang, J. Akhtman, L. Hanzo “Iterative Joint Channel Estimation and Multi-User Detection for Multiple-Antenna Aided OFDM Systems” IEEE transactions on wireless communications, vol. 6, no. 8, august 2007
  6. M. Jiang, J. Akhtman, L. Hanzo “Iterative Joint Channel Estimation and Multi-User Detection for Multiple-Antenna Aided OFDM Systems” IEEE transactions on wireless communications, vol. 6, no. 8, august 2007.
  7. Ming Jiang, Soon Xig Ng, Lajos Hanzo “Hybrid Iterative Multiuser Detection for Channel Coded Space Division Multiple Access OFDM Systems” IEEE transactions on vehicular technology, vol. 55, no. 1, january 2006.
  8. L. Hanzo, M. M¨ unster, B. J. Choi, and T. Keller, OFDM and MC-CDMA for Broadband Multi-User Communications, WLANs and Broadcasting.Piscataway, NJ: IEEE Press, New York: Wiley, 2003.
  9. Ming Jiang, S. Xin, and L. Hanzo, “Hybrid Iterative Multiuser Detection for Channe Coded Space Division Multiple Access OFDM Systems,” IEEE Transactions on Vehicular Technology, Vol. 55, No. 1, Jan. 2006.