International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Comparative Analysis of OFDM under FFT and DWT Based Image Transmission

Mr. Anshul Soni1, Mr. S.J. Basha2, Mr. Ashok Chandra Tiwari3
  1. Student, Dept of ECE, LNCT, Indore, India
  2. Professor, Dept of ECE, LNCT, Indore, India
  3. Professor, Dept OF ECE, LNCT, Indore, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

In This paper, the bit error rate analysis (BER) and peak signal to noise ratio performance (PSNR) of discrete wavelet transform (DWT)-OFDM system is compared with conventional fast fourier transform (FFT)-OFDM system for colour image transmission, here we use different error correcting codes like Reed Solomon codes, low density parity check codes (LDPC). The transmitted colour image is found to have retrieved effectively under noisy and fading situations with implementation of sum-product algorithm like fast Fourier transforms, discrete wavelet transforms.

Keywords
DWT, FFT, OFDM, Reed Solomon, LDPC.

I. INRODUCTION
In Today‟s communication environment, a demand for high data rate, reliable high speed. These requirement place indicative challenges to the parallel data transmission scheme which removes the problems faced with serial systems. High spectral efficiency and resilience to interference caused by multipath effects are the fundamentals to meet the requirements of today‟s wireless communication. The Orthogonal Frequency Division Multiplexing (OFDM) is a wideband multicarrier wireless digital communication technique that is based on block modulation. With the wireless multimedia applications becoming more and more popular, the required bit rate / high speed are achieved due to OFDM multicarrier transmissions.
The distribution of the data bits over many carriers means that fading will cause some bits to be received in error while others are received correctly. By using an error-correcting code, which adds extra bits at the transmitter, it is possible to correct many or all of the bits that were incorrectly received. The information carried by one of the vitiated carriers is corrected, because other information, which is related to it by the error correcting code, is transmitted in a different part of the multiplex.
OFDM systems
The basic principle of OFDM system is the division of the total frequency spectrum into many sub carriers. to achieve high spectral efficiency, the frequency responses of the sub-carriers are overlapping and orthogonal, hence the name OFDM.
Orthogonality between two signals means that the two coexisting signals are independent of each other in a specified time interval and do not interact with each other. The concept of orthogonal signals is essential for the understanding of Orthogonal Frequency Division Multiplexing (OFDM) system. In the normal sense, it may look like a miracle that one can separately demodulate overlapping carriers. This orthogonally can be completely maintained with a small price in loss in SNR , even though the signal passes through a time dispersive fading channel. By introducing a cyclic prefix (CP).
A block diagram of a base band OFDM system is shown in figure 1. The binary information is first grouped, coded and mapped according to the modulation in a “signal mapper”. After the serial to parallel conversion, an N- point inverse fast Fourier transform (IFFT) block transforms the data sequence in to time domain. Following the IFFT block, a cyclic extension of time length, chosen to be larger than the expected delay spread, is inserted to avoid inter-symbol and intercarrier interferences. At the receiver side, after passing through analog-to-digital converter (ADC) and removing the CP, the FFT is used to transform the data back to frequency domain. Lastly, the binary information data is obtained back after the demodulation and channel decoding.
Low-Density Parity-Check
LDPC was first invented by Gallager in his 1960 doctoral dissertation. After that in the year 1980 tanner introduced its graphical representation. In information theory, a low-density parity-check (LDPC) code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel, and is constructed using a sparse bipartite graph.
In LDPC the message block is transformed into a code block by multiplying it with a transform matrix. That means number of 1s in the transform matrix is less.
A (n,k ) LDPC encoder operates on an m x n size H matrix where m = n-k. It is low density because the number of 1s in each row wr is ≪ m and the number of 1s in each column wc is ≪ n. ALDPC is regular if wc is constant for every column and wr = wc (n/m) is also constant for every row. Otherwise it is irregular. In LDPC encoding, the code word ( c0,c1,....ck ) consists of the message bits ( m0,m1,....mk ) and some parity check bits and the equations are derived from H matrix in order to generate parity check equations can be written as:
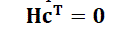image(1)
Where such mathematical manipulation can be performed with a generator matrix G. G is found from H with Gaussian elimination which can be written as follows:
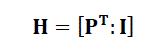image (2)
And G is G = [I : P]
Hence, c code word is found for message word x as follows c = xG = [x : xP ]
Tanner introduced an effective graphical representation for LDPC. Not only provide these graphs a complete representation of the code, they also help to describe the decoding algorithm.
Tanner graphs are bipartite graphs. The graphical representation for a typical (8,4) LDPC encoding is shown in Fig. 2. The graphical representation utilizes variable nodes (v-nodes) and check nodes (c-nodes). The graph has four c- nodes and eight v-nodes. The check node fi is connected to ci if hij of H is a 1. This is important to understand the decoding. Decoding tries to solve the (n−k) parity check equations of the H matrix. There are several algorithms defined to date and the most common ones are message passing algorithm, belief propagation algorithm and sum- product algorithm. In this paper, we have employed sum- product decoding algorithm as presented in [1].

II. SYSTEM DESIGN
Reed Solomon Code
Reed-Solomon (RS) codes are non-binary cyclic error- correcting codes introduced by Irving S.Reed and Gustave Solomon.
LDPC is the best coding technique as far as the coding gain is concerned but encoder and decoder design is complex on the other hand the reed Solomon can achieve high coding rate and have low complexity.
Reed-Solomon termed as a systematic way of constructing codes that could notice and correct many random symbol errors. By adding t check symbols to the data, it can detect up to t erroneous symbols or we can correct up to [t/2] symbols. Besides, RS codes are appropriate as multiple-burst bit-error correcting codes, as an another of b+1 consecutive bit errors can disturb at most two symbols of size b. The selection of t is depends on the designer of the code, and may be selected within wide limits.
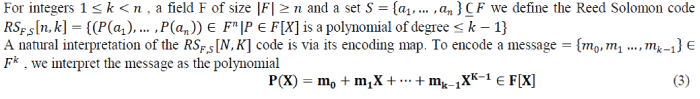image
We then evaluate the polynomial p at the points a1,..,an , we multiply the message vector , on the left by the n x k Vandermonde matrix
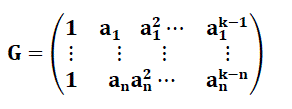image(4)
The matrix G is a generator matrix for RSF,S [N,K] , so we immediately obtain that Reed-Solomon codes are linear codes over F[7].
Fast Fourier Transform
The fast fourier transform is a faster version of discrete fourier transform (DFT). The FFT utilizes some clever algorithms to do same things as the DTF , but in much less time. The DFT is extremely important in the area of frequency analysis because it takes a discrete signal in the time domain and transforms that signal into its discrete frequency domain representation. Without a discrete-time to discrete-frequency transform we would not be able to compute the fourier transform with DSP based system.
It is the speed and discrete nature of the FFT. With the character of Discrete Fourier Transform (DFT), Discrete Cosine Transform (DCT) turn over the image edge to make the image transformed into the form of even function. It‟s one of the most common linear transformations in digital signal processing technology. Given a sequence of N samples f(n), indexed by n = 0 … . N − 1, the discrete fourier transform ( DFT) is define as F(k), where k = 0 … . N − 1:
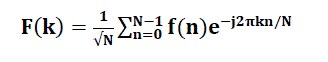image (5)
F(k) are often called the „ Fourier Coefficients‟ or „Harmonics‟.
The sequence f(n) can be calculated from F(K) using corresponding inverse transformation (IDFT) is defined as 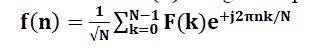image (6)
In general, both f(n) and F(k) are complex.
Conventionally, the sequences f(n) and F(k) is referred to as „ time domain‟ data and frequency domain‟ data respectively. Of course there is no reason why the samples in f(n) need be samples of a time dependant signal. For example, they could be spatial image sample ( though in such cases a 2 dimensional set would be more common).
For the sake of simplicity, when considering various Fast Fourier transform (FFT) algorithms, we shall ignore the scaling factors and simply define the FFT and Inverse FFT (IFFT) like this:
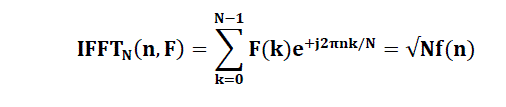image (7)
For display purposes, you probably want to cyclically translate the picture so that pixel (0,0). Which now contains frequency (ωx, ωy ) = (0,0), moves to the center of the image. And you probably want to display pixel values proportional to log(Magnitude) of each complex number. For colour images , do the above to each of the three channels (R,G and B) independently. FFT‟s are also used for synthesis of fractal textures and to create images with a given spectrum.
Discrete Wavelet Transform
Wavelet transform has been widely studied in signal processing in general and image compression in particular. Wavelet transform provides time frequency representation of the signal. The wavelet series is gust a sampled version of CWT and its computation may consume significant amount of time and resources, depending on the resolution required. The discrete wavelet transform (DWT), which is based on sub-band coding is found to yield a fast computation of wavelet transform. It is easy to implement and reduces the computation time and resources required. A discrete wavelet transform (DWT) is a sampled wavelet function. Rather than calculate the wavelet coefficients at every point, the DWT uses only a subset of positions and scales. This method results in an accurate and more efficient manner of a wavelet transform. The DWT is similar but more versatile that Fourier series. The DWT can be made periodic but it can also be applied to non-periodic transient signals.
The DWT of a signal is calculated by passing it through a series of filters. First the samples are passed through a low pass filter with impulse response 'g' resulting in a convolution of the two:
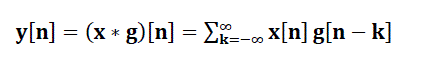image (8)
The signal is also decomposed simultaneously using a high-pass filter „h‟. The outputs giving the detail coefficients ( from the high pass filter) and approximation coefficients ( from the low-pass). It is important that the two filters are related to each other and they are known as a quadrature mirror filter.
However, since half the frequencies of the signal have now been removed, half the sample can be discard according to Nyquist‟s rule. The filter outputs are then sub-sampled by 2(Mallat‟s and the common notation is the opposite, �� − high pass and h- low pass);
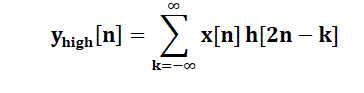image (9)
The wavelet transform has advantage of achieving both spatial and frequency localizations. Wavelet decomposition depends mainly on filter banks, typically the wavelet decomposition and reconstruction structures consist of filtering, decimation, and interpolation. Here figure shows two-channel wavelet structure.
Where H0, H1, G0 and G1 are the low decomposition, high decomposition, low reconstruction and high reconstruction filters, respectively.
Characteristics of DWT
1. The wavelet transform decomposes the image into three spatial direction i.e. horizontal, vertical and diagonal. Hence wavelets reflects the anisotropic properties of HVS more precisely.
2. Watermark detection at lower resolutions is computationally effective because ar every successive resolution level there are few frequency bands involved.
3. As LL band contains largest wavelet coefficients, scale factor is chosen accordingly up to 0.05 for LL and 0.005 for other bands. For this pair of values, there is no degradation in watermarked image.
4. High resolution sub bands locate edge and textures patterns in an image.

III. SIMULATION RESULTS
Figure-4 shows Graphical User Interface (GUI) in matlab.
Figure 5 through 8 shows BER analysis and PSNR performance of FFT source coding and DWT source coding with OFDM respectively.

IV. CONCLUSION
Here we can be concluded that deployment of a Different Compression techniques like discrete wavelet transforms in orthogonal frequency division multiplexing environment based wireless communication system, for discrete wavelet transform, is very much effective in proper identification and retrieval of transmitted digital image in noisy fading environment. In this paper, we evaluated the comparative performance of discrete wavelet transform(DWT) and fast fourier transform(FFT) source coding based orthogonal frequency division multiplexing system .We use different error correcting codes; Reed Solomon, LDPC, Conventional FFT and DWT. The simulation results shows that the DWT gives better result than the FFT. We found a constant higher PSNR in DWT. It shows greater efficiency & good BER performance also.
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
 
Figure 1 Figure 2 Figure 3 Figure 4
Figure 5 Figure 6 Figure 7 Figure 8
 

References