Comparative Study of Different Clustering
Algorithms

A.J.Patil; C.S.Patil; R.R.Karhe; M.A.Aher

Comparative Study of Different Clustering Algorithms

A.J.Patil¹, C.S.Patil², R.R.Karhe³, M.A.Aher⁴
Department of E&TC, SGDCOE (Jalgaon), Maharashtra, India^1,2,3,4

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents a detailed study and comparison of different clustering based image segmentation algorithms. The traditional clustering algorithms are the hard clustering algorithm and the soft clustering algorithm. We have compared the hard k-means algorithm with the soft fuzzy c- means (FCM) algorithm. To overcome the limitations of conventional FCM we have also studied Kernel fuzzy c- means (KFCM) algorithm in detail. The K-means algorithm is sensitive to noise and outliers so, an extension of K-means called as Fuzzy c- means (FCM) are introduced. FCM allows data points to belong to more than one cluster where each data point has a degree of membership of belonging to each cluster. The KFCM uses a mapping function and gives better performance than FCM in case of noise corrupted images.

Keywords

Clustering, Segmentation, K-means, FCM, KFCM.

INTRODUCTION

Image segmentation is the process of partitioning a digital image into multiple segments (sets of pixels, also known as super pixels). The requirement of the image segmentation is to extract some of the features which are more meaningful to represent the regions in that image. Image segmentation is mostly used to locate objects and boundaries (lines, curves, etc.) in images. In image segmentation, the label is assigned to every pixel which is further used to group them in to clusters using similarity between the labels. Cluster analysis or clustering is the process which groups objects of similar labels in one cluster and the dissimilar objects in another group or cluster. It has many applications in pattern recognition, data mining, medical imaging, document retrieval, grouping, machine learning situations. Clustering includes several algorithms depending on no. of iterations, grouping of similar objects in one cluster, its robustness to noise. The various algorithms are implemented to get the accurate cluster. The formation of the correct clusters is the major task in clustering which includes groups with small distances among the cluster members. Clustering can therefore be called as an multi-objective optimization problem. The appropriate clustering algorithm depends on the input data set and parameter settings which include the distance function to use, maximum no. of iterations, no. of clusters expected. And the proper results are achieved which are calculated on the basis of CAR(cluster accuracy rate).Clustering is actually not an automatic task but it can be called as an iterative process of knowledge discovery or interactive multi-objective optimization. It will often be necessary to modify data preprocessing and model parameters until the result achieves the desired properties.

Many clustering techniques or strategies have been implemented among which the two main categories of distinguishing the algorithms are the hard clustering and the soft clustering. The hard clustering allows a data point to belong to only one cluster and hence, it is called as hard boundary or crisp clustering. Whereas, the soft clustering includes a soft boundary where a data point may belong to more than one cluster depending on the distance criteria. It is modified by using a membership function to the hard clustering algorithm. The conventional clustering methods puts some limitations in case of images which may have poor contrast, intensity overlapping, limited spatial resolution, noise and intensity in homogeneities variations. So, to overcome this task the soft clustering algorithms are used in practice. The K-means algorithm is the type of hard clustering algorithms. The aim of this algorithm is to partition a given data set such that the data points in a same cluster are similar and the data point in different cluster are dissimilar to each other. It is given by Macqueen in 1967, is one of the simplest unsupervised learning algorithms that solve the well-known clustering problem. The requirement of k-means algorithm is that the clusters should be non-overlapping. K-means is simple and easy to implement and thus it is practically used in many image clustering applications. It classifies a given data set through a certain no. of clusters (assume k clusters) fixed a priori. The idea is to define kcentroids one for each cluster. These cluster centroids should be correctly placed. So, they should be placed far as possible to obtain the correct result. The technique to overcome the drawbacks of hard clustering algorithms is the soft clustering algorithms. In Soft clustering algorithms, the data point can belong to more than one cluster which depends on distance criteria. Fuzzy clustering is the type of soft boundary clustering where adata point belongs to more than one cluster. In fuzzy clustering a membership function is used for distance measure and it lies approximately between 0 and 1. In hard clustering, data is divided into different clusters, where each data object belongs to only one cluster and either a 0(do not belong to the cluster) or 1 (belong to the cluster) is assigned to specify that whether the data point belong to the cluster or not. In fuzzy clustering, the data elements can belong to more than one cluster, and each element is associated with a set of membership levels. It is an iterative algorithm which finds the solution of the objective function and depending on initialization it can find more than one solution. These indicate the strength of the association between that data element and a particular cluster. Fuzzy clustering is a process of assigning these membership levels, and then using them to assign data objects to one or more clusters. The conventional k-means and the FCM (fuzzy c-means) both are sensitive to noise and the outliers and hence advancements in fuzzy clustering are done by introducing a mapping function in KFCM (kernel fuzzy c-means).So, the Euclidian distance is replaced by kernel tricks. An overview and comparison of different fuzzy clustering algorithms is involved. In this paper we will see the drawbacks of the k-means clustering algorithm which are overcame by our FCM (Fuzzy c-means) clustering algorithm. The rest of this paper is organized as follows. Section II gives the literature survey. Section III reviews the hard clustering technique which is the K-means clustering algorithm. Section IV describes the soft clustering algorithm the fuzzy c- means algorithm. Section V gives the detailed study of KFCM (kernel fuzzy c-means) algorithm Section VI compares the clustering results and section VII concludes the clustering algorithms.

LITERATURE SURVEY

Even though there is an increasing interest in the use of clustering methods in pattern recognition [Anderberg1973], image processing [Jain and Flynn 1996] and information retrieval [Rasmussen 1992; Salton 1991], clustering has a rich history in other disciplines [Jain and Dubes 1988] such as biology, psychiatry, psychology, archaeology, geology, geography, and marketing. The K-means method is considered as one of the most popular and standard clustering methods. The goal of K-means is to partition a given dataset such that data points in a same cluster are similar and the data points in different clusters are dissimilar. It also requires that the clusters are non-overlapping. The clustering algorithms that satisfy the above requirements are classified as crisp clustering algorithms data clustering methods. On the other hand, algorithms that allow every data point to be assigned to more than one cluster are classified as fuzzy clustering methods. Fuzzy c-means method, proposed in Dunn (1973) and improved in Bezdek (1981), is a fuzzy clustering method that is analogous to the K-means method. The K-means method and fuzzy c-means method can be varied or improved by being applied with different choices of distance measures Mao and Jain (1996) Linde et al. (1980) Banerjee et al. (2005), and can be combined with other clustering techniques, for example, kernel methods Zhang et al. (2003), to achieve better results according to the nature of clustering problems.

THE K-MEANS ALGORITHM

K-means clustering is a method of vector quantization, which is known as the best squared error based clustering algorithm. The goal of K-means clustering is to start with an initial partition and provide patterns to clusters so that the error between the intensities of the pixels which belongs to the cluster and the mean gets reduced. And this is achieved by increasing the no. of iterations. In order to reduce the influence on the initial partition one can run the algorithm multiple times using different randomly generated initial partitions and can choose the best among them which has the smallest total squared distance.

The simplest and most commonly used algorithm, employing a squared error criterion is the K-means algorithm. This algorithm partitions the data into K clusters (C1, C2… CK), represented by their centers or means. The center of each cluster is calculated as the mean of all the instances belonging to that cluster. The K-means algorithm works well for the hyper spherical and the compact clusters. It may be viewed as a gradient-decent procedure, which begins with an initial set of K cluster-centers and iteratively updates it so as to decrease the error function. The complexity of T iterations of the K-means algorithm performed on a sample size of m instances, each characterized by N attributes, is: O(T*K*m*N). This linear complexity is one of the reasons for the popularity of the K-means algorithms. Even if the number of instances is substantially large k-means can be used to cluster large data sets, this algorithm is computationally attractive. Thus, the K-means algorithm has an advantage in comparison to other clustering methods (e.g. hierarchical clustering methods), which have non-linear complexity. The K-means Algorithm is summarized as follows:

Input: n objects (or points) and a number k.

Algorithm:

Step 1. Randomly place K points into the space which are represented by the objects that are being clustered. These initializes the centroids of the cluster.

Step 2. Assign each data object to the group that has the closest centroid.

Step 3. When all objects are assigned then the position of the k centroid are recalculated.

Step 4 . Repeat Steps 2 and 3 until the stopping criteria is met.

The stopping criterion of the K-means Algorithm is given as follows:

`1. There is no change in the members of all the clusters.

2. When the squared error is less than some small Threshold value α the squared error Se is given by,

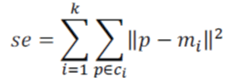Where mi is the mean of all instances in cluster cj

Se(j) < α. So, the K-means exactly achieves the local optimum and not the global optimum. As the k-means is a typical partitioning clustering algorithm it only works for the data sets of isotropic cluster. In addition, this algorithm is sensitive to noise and outliers which means that even if the object is quite far away from the centroid it is still considered in that cluster and distorts the cluster shape the k-means cannot guarantee convergence to a global optimum by its iteratively optimal procedure. The use of the K-means algorithm is often limited to numeric attributes.

Haung (1998) presented the K-prototypes algorithm, which is based on the K-means algorithm but removes numeric data limitations while preserving its efficiency. The algorithm clusters objects with numeric and categorical attributes in a way similar to the K-means algorithm. The similarity measure on numeric attributes is the square Euclidean distance; the similarity measure on the categorical attributes is the number of mismatches between objects and the cluster prototypes. Another partitioning algorithm, which attempts to minimize the SSE, is the K-medoids or PAM (partition around medoids). This algorithm is very similar to the K-means algorithm. It differs from the latter mainly in its representation of the different clusters. Each cluster is represented by the most centric object in the cluster, rather than by the implicit mean that may not belong to the cluster. The K-medoids method is more robust than the K-means algorithm in the presence of noise and outliers because a medoid is less affected by outliers. But the process is more costly as compared with the k-means algorithm. While k-means as well as k-medoids both need to specify the no. of clusters k.

FUZZY C-MEANS ALGORITHM

The most well-known fuzzy clustering algorithm is FCM (Fuzzy c-means), which is modified by Bezdek, an improvement of the original crisp or k-means clustering algorithm. Bezdek improved the cluster formation by including a fuzzification parameter (M) in the range [1, N], which determines the degree of fuzziness in the clusters. When M=1 it is called as crisp clustering of points. When M>1 is the degree of fuzziness among points in the decision space increases.

In FCM, given a data set of size n, X={x1,…,xn} and FCM groups x into c clusters by minimizing the weighted distance between the data and the cluster centers defined as:

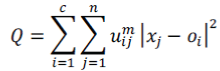uij is the membership of data xj belonging to cluster i. The FCM iteratively updates the prototypes [o1, o2, …,oc] and memberships uij through the equations below:

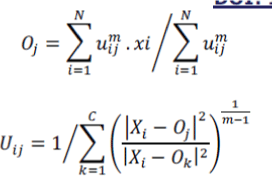This iteration is stopped until the difference between old membership values and the updated new ones is small enough. Finally based on resulting uij, we assign data xj into the cluster k, where Uik is the largest membership value in all Uij (i=1 to c).

Fuzzy c-means allows data points to be assigned into more than one cluster each data point has a degree of membership (or probability) of belonging to each cluster. Fuzzy c-means has been a very important tool for image processing in clustering objects in an image. The conventional clustering algorithms are the partitioning algorithms where each data object belongs to only single cluster. So, the clusters in k-means are said to be disjointed. Fuzzy clustering (Hoppner, 2005) extends this notion and suggests a soft clustering schema. Here, the pattern is represented by the membership function given to each cluster. The assignment of the pattern to the cluster larger membership values gives better performance. In a fuzzy clustering when the threshold of this membership values are obtained a hard clustering can be retrieved.

The most popular fuzzy clustering algorithm is the fuzzy c-means (FCM) algorithm. The FCM provides good results than the hard k-means algorithm but in case of avoiding local minima it converges to local minima of the squared error criteria. The most important problem in fuzzy clustering is to choose the membership function which has many choices based on similarity decomposition and cluster centroids. The family of the objective functions proposes a generalization for the FCM algorithm. Fuzzy means of or relating to a form of set theory and logic in which predicates may have degrees of applicability, rather than simple being true or false. The fuzzy logic is the logic of fuzzy sets; a fuzzy set has potentially an infinite range of truth valuesbetween zero and one. The central idea in fuzzy clustering is the non-unique partioning of the data in a collection of clusters.

The FCM Algorithm is as follows:

Step 1. Initialize U=[ujj] membership matrix, U(0)

Step 2. At k-step: calculate the centers vectors C(k)=[cj] with U(k) by,

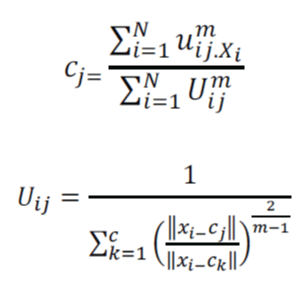Step 3. Update U (^k), U (^k+1)

Step 4. If|| U(^k+1>) −U^k|| < ∈ then STOP; otherwise return to step 2.

The FCM Algorithm should specify the following parameters the number of clusters, c, the ‘fuzziness’ exponent, m, the termination tolerance, ÃâÃâ, and the norm-inducing matrix, A. The fuzzy partition matrix U, must be initialized.

The determination of the no.of clusters c, is more important as it has more influence on the partitioning as compared with the other parameters. When clustering real data without any a priori information about the structures in the data,

one usually has to make assumptions about the number of underlying clusters. The chosen clustering algorithm then searches for c clusters, regardless of whether they are related present in the data or not. The two main approaches to determine the no. of clusters are the validity measures and the Iterative merging or insertion of clusters. Validity measures are scalar indices that assess the goodness of the obtained partition. The basic idea of cluster merging is to start with a sufficiently large number of clusters, and successively reduce this number by merging clusters that are similar (compatible) with respect to some well-defined criteria. The weighting exponent m is a rather important parameter as well, because it significantly influences the fuzziness of the resulting partition. As m approaches one from above, the partition becomes hard (μik∈ {0, 1}) and vi are ordinary means of the clusters. As m →∞, the partition becomes completely fuzzy (μik = 1/c) and the cluster means are all equal to the mean of Z.

The FCM algorithm stops iterating when the norm of the difference between U in two successive iterations is smaller than the termination parameter ÃâÃâ. For the maximum norm matrix the usual choice is 0.001, even though 0.001 workswell in most cases, reducing the computation time complexity. A common choice is A = I, which gives the standard Euclidean norm. The norm influences the clustering criterion by changing the measure of dissimilarity. The Euclidean norm induces hyper spherical clusters (surfaces of constant membership are hyper spheres). Both the diagonal and the Mahalanobis norm generate hyper ellipsoidal clusters.

KERNEL FUZZY C-MEANS

The FCM is the soft extension of the traditional hard c-means clustering. Each cluster was considered as fuzzy set and the membership function measures the possibility that each training vector belongs to a cluster.so, the vectors may be assigned to multiple clusters. Thus, it overcomes some drawbacks of hard clustering but it is effective only when the data is non-overlapping. So, we use the Kernel-based fuzzy C-means algorithm (KFCM). In KFCM, both the data and the cluster centers are mapped from the original space to a new space by ∅,So, the objective function is given as follows:

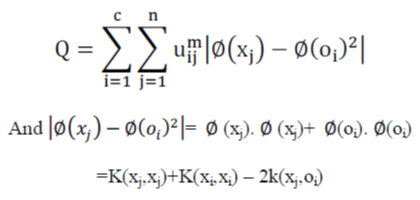We reformulate the objective function as,

Because we know k, the new Q has explicit formulation, so we can optimize it anyway.

The Kernel fuzzy C-means (KFCM) Algorithm is as follows:

Step 1.Fix c, tmax, m>1 and ÃâÃâ>0 for some positive constant.

Step 2. Initialize the memberships , C, m.

Step 3. For t=1, 2,……..,tmax do

(a) Update all prototype with the equation as,

The cluster center ci can be obtained from:

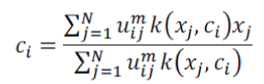(b) Update all memberships with equation as,

The membership matrix U can be obtained from:

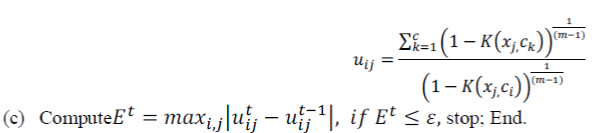CLUSTERING RESULTS

The original image is taken which is the image of a synthetic test image, with two classes of gray levels values 0 and 255. We have corrupted it with 15% salt and pepper noise and the results of FCM and KFCM are obtained.

The clustering results of the different clustering algorithms are shown in figure 2.FCM(Fuzzy c-means) and KFCM(Kernel fuzzy c- means)algorithms are compared by taking two images the synthetic test image and the brain image and the corresponding clustering results are shown in figure 2 and figure 3.

Figure 2 illustrates the clustering results of an corrupted image Original image [Fig.2 (a)], corrupted image [Fig.2 (b)], FCM result [Fig. 2(c)], KFCM result [Fig.2 (d)].

We can observe from fig 2 that both the FCM and KFCM provides the image segmentation even if the image is corrupted and the noise gets reduced to much extent when compared with the corrupted image.The FCM removes the noise and gives the clustering result of the image and the KFCM reduced the noise to more extent than FCM and provides better clustering.

The next image is the image of brain. In this image 3% Gaussian noise is added to the original image and the results for FCM and KFCM are observed.

In this, the original image [Fig.3 (a)], is the image of a brain then it is corrupted by 5% Gaussian noise [Fig.3 (b)], and the clustering results obtained are shown in [Fig.3 (c)] and [Fig.3 (d)]. From the results we can observe that the clustering accuracy of KFCM is better than FCM. Thus, we can see from the above two experiments that by using a mapping function the KFCM gives better performance when compared with the FCM.

CONCLUSION

Clustering techniques are mostly unsupervised methods that can be used to organize data into groups based on similarities among the single data items. Most clusteringalgorithms do not depend upon assumptions that match to the traditional statistical methods, such as the distribution of the statistical data. Therefore, in the cases where the prior knowledge exists they led very important role. In this paper, we discussed the hard k-means algorithm which gives better efficiency but are more sensitive to noise and outliers. The soft Clustering algorithm introduces a vector which expresses the percentage of belonging of a point to each cluster. FCM (Fuzzy c-means) may converge faster than hard k-means, but the computational complexity increases. The FCM works well in cases where the data is non-overlapping. For non-linear versions of FCM the KFCM gives better results. It does not the need of desired number of clusters in advance; it determines the number of clusters in the data and yields better performance than FCM in case of noise. Hence the clustering algorithms had many applications in segmentation, magnetic resonance, imaging (MRI), analysis of network traffic, Fourier transform infrared spectroscopy (FTIR).

Figures at a glance


Figure 1	Figure 2	Figure 3

References

Pallavi Thakur, ChelpaLingam, “Generalized Spatial Kernel based Fuzzy C-Means Clustering Algorithm for Image Segmentation, ” IJSR Vol. 2 issue may 2013.
Yang Y., Zheng Ch., and Lin P., "Fuzzy c-means Clustering Algorithm with a Novel PenaltyTerm for Image Segmentation", Opto-Electronics Review, Vol.13, No.4, Pp.309-315, 2005.
Bezdek J.C. “Pattern Recognition with Fuzzy Objective Function Algorithms”ÃÂ¯ÃÂ¼ÃÅ½Plenum Press, New York, 1981.
J. C. Dunn, "A Fuzzy Relative of the ISODATA Process and its Use in Detecting Compact, Well-Separated Clusters," J. Cybernetics, Vol. 3, Pp. 32-57,1973.
Wu Z, Xie,W.X Yu J.P. “Fuzzy C-means Clustering Algorithm Based on Kernel Method” In: Proceedings of Fifth International Conference on Computational Intelligence and Multimedia Applications,Pp 49-56,2003.
SteliosKrinidis and VassiliosChatzis,” A Robust Fuzzy Local Information C-Means Clustering Algorithm”, IEEE Transactions on Image Processing, Vol. 19, No. 5, MAY 2010.
Gimiami M, “Mercer kernel based clustering in feature space”, IEEE Transactions on Neural Networks, Vol. 13, No. 3, Pp780-784, 2002.
Chun-yan Yu, Ying Li, Ai-lian Liu, Jing-hong Liu, “A Novel Modified Kernel Fuzzy C-Means Clustering Algorithm on Image Segmentation”, IEEE International Conference on Computational Science and Engineering CSE/I-SPAN/IUCC 2011.
Anderberg M. R., 1973. Cluster Analysis for Applications. Academic Press .
Pratt W., 1991. Digital Image Processing, John Wiley & Sons, New York.
Coleman G. B. and H. C. Andrews, 1979. “Image segmentation by clustering”, Proc IEEE 67:773–785.
Cheng, H. D, X. H. Jiang, Y. Sun and J. Wang, 2001. Color image segmentation: advances and prospects, Pattern Recognition, Vol.34, 2259– 2281 .
Y. C. Liaw, J. Z. C. Lai, and W. Lo, “Image restoration of compressed image using classified vector quantization,” Pattern Recognition, Vol. 35, 2002, pp. 181-192.
J. Z. C. Lai, T. J. Huang, and Y. C. Liaw, “A fast k-means clustering algorithm using cluster center displacement,” Pattern Recognition, Vol. 42, 2009, pp. 2551-2556.
R. L. Cannon, J. V. Dave, and J. C. Bezdek, “Efficient implementation of the fuzzy c-means clustering algorithm,” IEEE Transactions on PAMI, Vol. 8, 1986, pp. 248-255.