International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Comparison of GA and PSO Algorithms in Cascaded Multilevel Inverter Using Selective Harmonic Elimination PWM Technique

M.Mythili1, N.Kayalvizhi2
  1. PG Scholar [PED], Dept. of EEE, K.S.Rangasamy College of Technology, Tiruchengode, Tamilnadu, India 1
  2. Assistant Professor, Dept. of EEE, K.S.Rangasamy College of Technology, Tiruchengode, Tamilnadu, India 2
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The Selective Harmonic Elimination (SHE) technique is the fundamental switching frequency scheme which is used to eliminate specific order harmonics. In this paper, the elimination of low order harmonics in cascaded multilevel inverter with equal DC sources is proposed. The modulation strategy used here is SHEPWM in which non linear equations that characterize the low order harmonics are obtained. The equations are solved using Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) algorithm to obtain the switching angles which are used to eliminate the harmonics. Comparison of GA and PSO algorithms are done using MATLAB software to know the effectiveness of getting optimized switching angles.

Keywords
Cascaded Multilevel Inverter, Genetic Algorithm, Particle Swarm Optimization, Harmonic Elimination

INTRODUCTION
Generally the output voltage of the inverters must be sinusoidal. However the waveforms of practical inverters are nonsinusoidal and contain certain harmonics. So to synthesize a near sinusoidal component and to reduce the harmonic distortion multilevel inverters are emerged. It is a promising technology to interface the battery packs in electric vehic`les because of possibility of high power rating without the use of transformer. Nowadays, there exist three commercial topologies of multilevel voltage-source inverters: neutral point clamped (NPC) [1], cascaded H-bridge (CHB), and flying capacitors (FCs) [2].
Among these inverter topologies, cascaded multilevel inverter reaches the higher output voltage and power levels and the higher reliability due to its modular topology. Cascaded multilevel inverters are based on a series connection of several single-phase inverters. This structure is capable of reaching medium output voltage levels using only standard low-voltage components. Typically, it is necessary to connect three to ten inverters in series to reach the required output voltage. These converters also feature a high modularity degree because each inverter can be seen as a module with similar circuit topology, control structure, and modulation [3].
There are many types of Pulse Width Modulation (PWM) techniques for multilevel inverter. In this fundamental switching frequency strategy are used for cascaded multilevel inverter. The fundamental switching strategy used here is Selective Harmonic Elimination PWM (SHEPWM) [4]. This is a modulation strategy which is used to eliminate the specific low order harmonics. The solution of SHEPWM contains non linear transcendental equations. The equations are solved by numerical iterative methods in the literature. This method is very complex and time consuming. The methods used are Newton Raphson and resultant theory [5].Nowadays the optimization algorithms are used for solving the equations which are used to obtain the switching angles. The optimization algorithms used in the literature are Genetic Algorithm (GA) [6]-[7], Ant colony optimization [8] and particle swarm optimization [9].
In this paper, GA and PSO are used to solve the nonlinear equations obtained from SHEPWM strategy. The optimized switching angles can be obtained using these algorithms. The comparison of two algorithms is done to find the effective results.

MULTILEVEL INVERTERS
Multilevel inverter is used to synthesize a near sinusoidal wave from several levels of DC Sources. As number of levels increases, the synthesized output waveform has more steps, which provides a staircase wave that approaches a desired waveform. Also, as steps are added to waveform the number of voltage levels increases thus the harmonic distortion of the output waveform decreases and approaches to zero.
A. Multilevel Inverter Topology
A cascaded multilevel inverter topology is used as it has fewer components, absence of extra clamping diodes or voltage balancing capacitors and easy adjustment of number of output voltage levels. The general structure of sevenlevel cascaded multilevel inverter is shown in Fig.1.
It consists of three full bridge inverters connected in series. Each full bridge consists of four switching devices that can make the output voltage either positive or negative polarity, or simply zero depending on the switching condition of the switches in the circuit. This multilevel inverter employs three voltage sources of equal magnitude. The numbers of sources S are related to number of levels n in the output voltage by,
image(1)
Here number of sources equal three, hence number of levels in the output voltage is seven. The output waveform of seven-level multilevel inverter is shown in Fig.2.The different levels of voltage are also specified in the figure.
B. Selective Harmonic Elimination PWM Strategy
The Selective Harmonic Elimination PWM technique is based on fundamental frequency switching theory and dependent on the elimination of defined harmonic content orders. The main idea of this method is based on defining the switching angles of harmonic orders to eliminate and obtaining the Fourier series expansion of output voltage. This allows lower switching frequencies to be used which led to lower losses and higher efficiency. In general Fourier series is given by,
image(2)
In this case Fourier series expansion of output voltage waveform is given by,
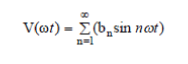image(3)
Where
(due to quarter wave symmetry)
For quasi square wave,
image(4)
On solving we get,
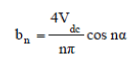image(5)
For 7-level cascaded multilevel inverter for three dc sources equation (5) is given as,
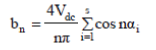image(6)
Where n=1, 5, 7 and s=3 which represents number of DC sources. The objective of SHEPWM is to eliminate lower order harmonics while remaining harmonics can be removed with filter. In this number of harmonics that can be eliminated is equal to s-1 i.e.,2 so fifth and seventh harmonics are taken. So, to satisfy the fundamental harmonic component and eliminate the fifth and seventh harmonics, three nonlinear equations with three angles are provided in,
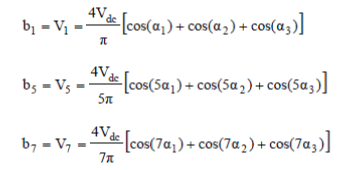image(7)
To eliminate fifth and seventh harmonic V5 and V7 are set to zero in the above equations. To determine the switching angles the following equations must be solved,
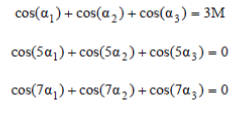image(8)
Here M represents modulation index varies from 0 to 1.The switching angles α1, α2 and α3 must be less than π/2. The equations are solved by Newton Raphson (NR) method and resultant theory in the literature. But it is time consuming and needs initial guess for solving the equations. Hence evolutionary algorithms are used for solving this type of non linear equations.

EVOLUTIONARY ALGORITHMS
Evolutionary algorithms (EAs) are stochastic search methods that mimic the metaphor of natural biological evolution and/or the social behavior of species. Examples include how ants find the shortest route to a source of food and how birds find their destination during migration.
A. Proposed Genetic Algorithm
The first evolutionary based technique introduced in the literature was the Genetic Algorithms (GAs). GA was developed based on the Darwinian’s principle of the survival of the fittest and the natural process of evolution through reproduction. The steps for formulating a problem and applying a proposed GA for obtaining switching angles are as follows:
1. Select binary or floating point strings.
2. Find the number of variables specific to the problem; this number will be the number of genes in a chromosome. In this application the number of variables is the number of controllable switching angles which is the number of H-bridges in a cascaded multilevel inverter. A seven-level inverter requires three H-bridges; thus, each chromosome for this application will have three switching angles.
3. Set a population size and initialize the population. The population used here is 20 chromosomes, each containing three switching angles. The population is initialized with random angles between 0 degree and 90 degree taking into consideration the quarter wave symmetry of the output voltage waveform.
4. The most important item for the GA to evaluate the fitness of each chromosome. The objective of this study is to minimize specified harmonics; therefore the fitness function has to be related to these harmonics. The harmonics taken here are fifth and seventh harmonic hence fitness function is,
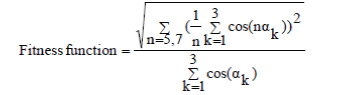image(13)
5. The GA is usually set to run for a certain number of iterations (100 in this case) to find an answer. After the first iteration, fitness values are used to determine new offspring. These go through crossover and mutation operations and a new population is created which goes through the same cycle starting from fitness evaluation until the solution is found that satisfy the constraints which are from equation (10)-(12). These are the steps used for solving nonlinear equations using Genetic Algorithm.
B. Proposed Particle Swarm Optimization
Particle swarm optimization is a collective system that has been applied successfully to wide variety of search and optimization problems. It is a machine learning technique loosely inspired by birds flocking in search of food. The PSO is implemented here to solve the nonlinear equations obtained from SHEPWM. This is achieved by minimizing the objective function which characterizes the specific order harmonics. Here each particle is characterized by the value of the variable and corresponding value of the function. The solution of PSO algorithm is taken as the switching angles for seven-level multilevel inverter. The step by step procedure for implementing PSO is as follows:
1. The parameters of the algorithm such as population size (=20 particles) and maximum number of iterations are initialized.
2. Each particle in the population is randomly initialized randomly between 0 and  /2.
3. Initialize the velocity, personal best, global best and iteration count.
4. Evaluate the fitness value at each particle position which is given by equation (13).
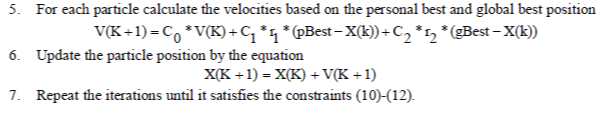image

IMPLEMENTATION OF GA AND PSO IN MATLAB
The seven-level cascaded multilevel inverter using GA and PSO is implemented in simulation using MATLAB/Simulink. The m-file is used to write the algorithm codes for solving the equations and to obtain the switching angles. The obtained switching angles are implemented in Simulink using Simpower Systems toolbox. The switching angle values obtained for various modulation indexes for GA and PSO are shown below in Fig.3 and 4.
The GA algorithm has obtained the switching angles by varying the modulation index M from 0.4-0.8. For the other M, it has no solution. In Fig.4, the switching angles obtained from PSO varies from M is 0.1 -1. It has obtained solutions for wide range of modulation indexes. The switching angles obtained from PSO and GA shown in Figures above are used to trigger the seven-level multilevel inverter.

RESULTS AND DISCUSSION
A. Simulation Results
The simulation model of single phase seven level inverter is shown in Fig.5. It consists of three full bridge inverters connected in series. The switching pulses are given from the switching circuit to the IGBT switches. The single phase AC output is given to the load. The input voltages for all the three full bridge inverters are same.
The input voltage given for multilevel inverter is 24V. The switching pulses for MOSFET switches are shown in Fig.6. The switching pulses G1, G5 and G9 are used to trigger the MOSFET switches for positive cycle. The switching pulses G3, G7 and G11 are used to trigger the MOSFET switches for negative cycle.
The output voltage of the seven-level cascaded multilevel inverter is shown in Fig.7. The output voltage is 72V which is thrice the input voltage. The seven levels of the output are obtained which are 24 V, 48 V and 72 V which are both positive and negative polarity
The output current waveform for single phase seven-level inverter is shown in Fig.8. As RL load is connected it synthesizes a near sinusoidal waveform. The output current obtained is 0.72 A.
The FFT analysis is done to estimate the THD value. The FFT analysis for the output voltage waveform obtained from GA and PSO is shown in Fig.9 and 10. It displays the harmonic spectrum of the output voltage.
The THD obtained from PSO is low compared to GA but the seventh harmonic in PSO violates the IEEE standard of individual harmonic distortion which must be less than 3%. Hence the switching angles obtained from GA are implemented in hardware to validate the simulation results.
B. Experimental Results
For verifying GA solutions, single phase hardware prototype seven-level multilevel inverter was built. It consists of three full bridge inverters that are connected in series form. DC source voltage of each H-bridge inverter is constant and is selected to be 24 V. The frequency of the output is 50 Hz. The switching angles obtained from GA are used to trigger the MOSFET switches in cascaded multilevel inverter using dsPIC controller. The Fig.11 shows the output voltage waveform obtained from Digital Storage Oscilloscope for Modulation Index M=0.8. It has less distortion and hence less THD which validates the simulation results.

CONCLUSION
In this paper a method based on genetic algorithm and particle swarm optimization algorithm are used to solve the non linear transcendental equations obtained from SHEPWM strategy. These equations determine the switching angles which are used to minimize the THD. The THD value obtained from PSO is 10.84% but fifth and seventh harmonic is not less than 3% hence GA are used to obtain experimental results. The effectiveness of the applied method is verified using the simulation results. It is also implemented in hardware. This work can be extended to multilevel inverters with reduced number of switches for further enhancement of output waveform.

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 5 Figure 6 Figure 7 Figure 8
Figure 5 Figure 6 Figure 7 Figure 8
Figure 9 Figure 10 Figure 11
Figure 9 Figure 10 Figure 11
 

References
  1. A. Nabae, I. Takahashi, and H. Akagi, “A new neutral-point-clamped PWM inverter,” IEEE Transactions on Industrial Applications, Vol.17, no. 5, pp. 518–523, Sep./Oct. 1981.
  2. T. A. Meynard, H. Foch, P. Thomas, J. Courault, R. Jakob, and M. Nahrstaedt, “Multicell converters: Basic concepts and industry applications,” IEEE Transactions on Industrial Electronics, Vol. 49, no. 5, pp. 955–964,Oct. 2002.
  3. Mariusz Malinowski, K. Gopakumar, Jose Rodriguez, and Marcelo A. Perez, “A Survey on Cascaded Multilevel Inverters” IEEE Transactions on Industrial Electronics, Vol. 57, no. 7, pp.2197-2206, July 2010.
  4. Li Li, DariuszCzarkowski, Yaguang Liu, and PragasenPillay, “Multilevel Selective Harmonic Elimination PWM Technique in Series Connected Voltage Inverters” IEEE Transactions on Industry Applications, Vol. 36, no. 1, pp.160-170, Jan./Feb.2000.
  5. JagdishKumar,Biswarup Das, and PramodAgarwal, “Harmonic Reduction Technique for a Cascade Multilevel Inverter” International Journal of Recent Trends in Engineering, Vol.1, no. 3, May 2009.
  6. K. L. Shi and Hui Li ,”Optimized PWM Strategy Based on Genetic Algorithms” IEEE Transactions on Industrial Electronics, Vol. 52, no. 5, pp.1458-1461, Oct. 2005.
  7. KinattingalSundareswaran, Krishna Jayant, and T. N. Shanavas, “Inverter Harmonic Elimination Through a Colony of Continuously Exploring Ants” IEEE Transactions on Industrial Electronics, Vol. 54, no. 5, pp.2558-2565, Oct.2007.
  8. MehrdadTarafdarHagh , Hassan Taghizadeh, and KavehRazi, “Harmonic Minimization in Multilevel Inverters Using Modified Species Based Particle Swarm Optimization” IEEE Transactions on Power Electronics, Vol. 24, no.10, pp.2259-2267,Oct. 2009
  9. Jose Rodriguez, Jih-Sheng Lai, and Fang ZhengPeng, “Multilevel Inverters: A Survey of Topologies, Controls, and Applications” IEEE Transactions on Industrial Electronics, Vol. 49, no. 4, pp.724-738, Aug.2002.
  10. Andreypopov (2005) Genetic Algorithms for Optimization User Manual.
  11. Mythili. M and Kayalvizhi.N, “THD Minimization in Single Phase Symmetrical Cascaded Multilevel Inverter Using Programmed PWM Technique” International Journal of Scientific and Engineering Research, vol. 4, Issue 11, pp.1567-1572, Nov. 2013.
  12. Jin Wang and DamounAhmadi, “A Precise and Practical Harmonic Elimination Method for Multilevel Inverters” IEEE Transactions on Industry Applications, Vol. 46, no. 2, pp.857-865, March/April 2010.
  13. Jason R. Wells, Brett M. Nee, Patrick L. Chapman and Philip T. Krein , “Selective Harmonic Control: A General Problem Formulation and Selected Solutions” IEEE Transactions on Power Electronics, Vol. 20, no. 6, pp.1337-1345, Nov.2005.