ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| *Shashank Mishra1, G.S. Tripathi2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In recent years, Artificial Neural Network has been the topic of great interest in the field of Wireless Communication in different ways. To enhance the accuracy of location estimation, we propose the various neural network algorithms i.e. Resilient back-propagation (Rprop), Levenburg-Marquardt (LM), Conjugate gradient with Polak-Ribiere Updates (CGP), Conjugate gradient with Fletcher-Reeves Updates (CGF) utilizing the time of arrival (TOA) measurement information in presence of NLOS error to locate the mobile station (MS) with three base station available. Computer simulations have been performed by using Neural Network Toolbox for MATLAB and then performance of various algorithms has been compared in terms of root mean square (RMS) error.
Keywords |
||||||||
| Wireless Location; TOA; NLOS; Artificial Neural Network; RMS error; LM; Rprop; CGP; CGF. | ||||||||
INTRODUCTION |
||||||||
| Location estimation of mobile users in cellular phone networks is becoming more prominent as the number of emergency calls originating from mobile stations (MS). There are number of different radio frequency based techniques that can be used for wireless position location. The implementation of various Artificial The objective is, how efficiently the problem of tracking a Mobile station (MS) based on some parameters has been of interest for some time. Many Wireless Location techniques have been used in recent years [1]. Some of them are Time of Arrival (TOA), Angle of Arrival (AOA), Time of Difference Arrival (TDOA), Received Signal Strength (RSS), Hybrid TOA/AOA[2]. Among them TOA is most widely used technology for Location Estimation of Mobile Station (MS). | ||||||||
| The accuracy of the location estimation in wireless communication vastly depends on the propagation conditions of the wireless channels. The Non-line-of-sight (NLOS) greatly affects the accuracy of MS location estimation. Precise position accuracy can be achieved if LOS propagation exists between the MS and each participating Base Station (BS). But LOS paths are usually available in urban and suburban areas. Different reflection and diffraction between the MS and BSs results in NLOS propagation. Due to NLOS propagation, there are biases in time and angle measurement. So, it is very necessary to remove NLOS error before applying the time and angle measurement in location estimation and tracking. | ||||||||
| Different Artificial Neural Network Techniques have been widely used in solving the problem of non-linear relationships. In recent times, various algorithms have been used in localization. Three networks are used by utilizing distance measurements, i.e. multi layer perceptron (MLP), radial basis function (RBF) and recurrent neural network, for indoor location estimation in wireless sensor network. Similarly, neural network algorithms have been also been applied to wireless local area network (WLAN), in which received signal strength (RSS) measurements related to known position is utilized for localization. | ||||||||
| In this paper, various neural network algorithms have been used for the location estimation of mobile station (MS) and after the simulation, results related to various algorithms have been compared with each other after proper computer simulation. | ||||||||
TIME OF ARRIVAL LOCATION ESTIMATION APPROACH |
||||||||
| Available measurements are either network-assisted or mobile-assisted, using uplink or downlink information [3]. TOA technique Position estimation by the triangulation is based on knowing the distance from the mobile to at least three base stations in the line of sight (LOS).Subtracting the TOA measurements from the two BS’s. The base station determines the time signal takes from the source to the receiver either on the uplink or the downlink. We must need at least 3 Bs’s to estimate position. Suppose the coordinates for BS1, BS2, BS3 are (X1, Y1), (X2, Y2)=(X2,0), and (X3,Y3) respectively. Then the distance between one of the base station and the MS can be written as follows: | ||||||||
| Where c is the speed of signal propagation (i.e. speed of light), (x, y) and are the location of the MS and BSi respectively. If is the initial estimated position then | ||||||||
| By linearizing the TOA equations using Taylor Series expansion and retaining the first two terms, the equation can be written as: | ||||||||
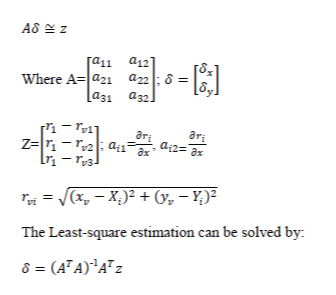 |
||||||||
| The recursive procedure with initial guess is used to predict the MS position and then repeating the computation in the iteration. | ||||||||
| NLOS propagation is often the prime cause of error in positioning, thus make mobile positioning challenging. In urban and suburban areas, the direct Line of Sight between the BS and MS may be blocked by various obstacles. The reflection and diffraction from the obstacles reach the receiving nodes. Therefore, delay of the first arriving signal does not estimate the true TOA because the signal travels an extra distance. This positive bias is called the NLOS error present in the estimated time delay [4]. Without having any information about NLOS error, precise location estimation is impossible. Wylie and Holtz man [5] observed that the variance of the TOA measurement in the LOS case is usually much greater than that in the LOS case. They used this difference in the variance to identify NLOS propagation and proposed a simple LOS reconstruction Algorithms to reduce the location estimation error. | ||||||||
VARIOUS NEURAL NETWORK ALGORITHMS |
||||||||
| A. BACK PROPAGATION ALGORITHM | ||||||||
| Back Propagation is a gradient descent algorithm in which the network weights are moved along the negative of the gradient of the performance function. The term Back Propagation refers to the manner in which the gradient is computed for nonlinear multilayer networks. BP neural network consists of an input layer, an output layer, and one or more hidden layers. To compute the net input neuron, each input connected to the neuron multiplied by its corresponding weight to form a weighted sum, which is added to bias associated with neuron j. Thus, the net input ïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿý to the neuron j can be written as: | ||||||||
| Where = weight from neuron I to neuron j | ||||||||
| = output of the neuron from the previous layer | ||||||||
| = bias of the neuron j | ||||||||
| In each neuron, the weighted inputs from other neurons as well as a bias term are summed up, and then transferred to the activation function. An activation function is used to transform the output variable, so it will fall into an acceptable range. | ||||||||
| B. CONJUGATE GRADIENT ALGORITHM | ||||||||
| Conjugate gradient algorithm, unlike BPNN algorithm, update weights along conjugate direction and produces generally faster convergence than that of steepest descent in BPNN algorithm. In this algorithm, step size can be adjusted for every epoch (iteration). In the first iteration, the algorithms initialize the network by searching in the negative of the gradient: | ||||||||
| Where, is initial search gradient and is initial gradient. Now we can find out the optimal distance to move along the current search direction using ine search: | ||||||||
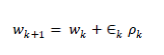 |
||||||||
| Where is current weight vector, +1 is next weight vector, minimizes the error function along the search direction. In next epochs, the search direction is determined by the combination of the new gradient and the weighting value of previous search direction: | ||||||||
| Where is the current gradient, is weighing value and −1 is previous search direction. | ||||||||
| C. RPROP ALGORITHM | ||||||||
| The Rprop algorithm provides faster training time and convergence rate and has the capability to escape from local minima. Rprop is a first-order algorithm and its time and memory required is only linear proportional to the number of parameters to optimize [4]. The Rprop algorithm is probably the easiest one to adjust the learning rule. Although there are a large number of adjustable parameters for Rprop, majority of these parameters can be set by default values. The slight variations in any of these parameters would not affect the convergence time. Rprop is an efficient training scheme which performs a direct adaptation of the weighting factors based on local gradient information. The principle of Rprop is to eliminate the harmful effects of the partial derivative magnitudes to calculate the weight. In the Rprop training algorithm, only the sign of the derivative is considered to determine the direction of the updated weight. The magnitude of the derivative has no effect on the weight updated. | ||||||||
| D. LM ALGORITHM | ||||||||
| The LM algorithm not only has the fastest convergence but also train a neural network 10–100 times faster than the BPNN algorithm. Another advantage of this algorithm is especially useful when a very accurate training is required. It is an approximation to the Newton’s method [5] and like the Quasi-Newton methods, the LM algorithm can approach the second order training speed without having to compute the Hessian matrix. Therefore, it is a widely used advanced optimization algorithm that outperforms the steepest descent algorithm. Hence, the LM algorithm provides a good compromise between the speed of Gauss-Newton and the guaranteed convergence of the steepest descent methods. Thus LM is much faster and more powerful than the gradient descent algorithm. | ||||||||
| MEASUREMENT BASED ON NEURAL NETWORK | ||||||||
| The distance measured from each base station can form a circle with each BS at its center. The position of MS can be estimated by the intersection of three circles formed by three BSs. The equations describing the circle for TOA shown in figure 1are as follows: | ||||||||
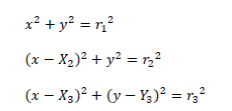 |
||||||||
| The equations shown above are in the absence of NLOS propagation. But in case of NLOS error, three circles will intersect at 3 different points. As we know that NLOS is always positive due to the excess path length, the measurements will always appears as a positive bias [6] i.e. greater than the true values. In such conditions, the equations mentioned above can be rewritten as: | ||||||||
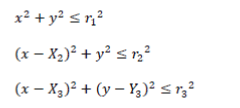 |
||||||||
| In order to locate the MS with given data, we have to train our neural network [7]. The steps which we have to follow to train our network are as follows: | ||||||||
| 1. Establish an input data set for training by using these feasible intersections. | ||||||||
| 2. Apply BP training algorithms with training set having input patterns with required output patterns. | ||||||||
| 3. During training procedure, BP neural network repeats and adjusts the weights of the connections in the network. | ||||||||
| 4. In the training procedure, our main objective is to minimize the difference between the actual MS location and desired MS location. | ||||||||
| 5. After successful training, new input patterns can be used to predict the MS location. | ||||||||
RESULTS AND DISCUSSION |
||||||||
| Computer simulation has been performed using Neural Network for MATLAB to examine the efficiency of various algorithms. The parameters such as numbers of hidden neurons and training epochs must be set before we apply network to estimate location. The coordinates 3 Base stations namely BS1, BS2, BS2 are set to (0,0), (1550m, 600m) and (700m, 1000m) respectively. Position accuracy is measured in terms of root-mean-square (RMS) error between the actual MS location and Desired MS location. The performance of different algorithms i.e. Resilient back-propagation (Rprop), Levenburg-Marquardt (LM), Conjugate gradient with Polak-Ribiere Updates (CGP), Conjugate gradient with Fletcher- Reeves Updates (CGF) have been compared in Figure 2. | ||||||||
| To Avoid overtraining, test data was used to check whether the network is over trained or not. The first N/2 training iterations are used for training andthe last N/2 for test data. The performance comparison based on test data with upper bound 500 m is shown in figure 3. We can observe that network gives good prediction for both training and test data. Thus, overtraining is not affecting the network model. | ||||||||
| The number of hidden neurons also plays an important in training of network. Very few hidden neurons can cause big errors. The general rule for choosing the number of neurons hidden layer are: (i) 0.5(p + q), (ii) p, (iii) 2p + 1, (iv) 3p + 1, where p and q are the input and output hidden neurons respectively [].It is clear from the figure 4 that RMS error converged to the same minimum value for different hidden layer neurons. For the best performance, 0.5(p + q) hidden neurons and 1000 epochs for both training and testing data are proposed by us. | ||||||||
| After observing the performance comparison, it is pretty clear that positioning accuracy of LM and Rprop algorithm is better that of CGF and CGP algorithm. | ||||||||
CONCLUSION |
||||||||
| In this paper, we propose different neural network algorithms for location estimation of Mobile Station (MS) based on Time of Arrival (TOA) in presence of NLOS errors and compare the performance of algorithms in terms of RMS error for both training and testing data. After the efficient training, the proposed algorithm can reduce NLOS error and one can obtain more accurate position estimation. In future, many other efficient neural network algorithms can be used for different purposes in wireless communication. | ||||||||
Figures at a glance |
||||||||
|
||||||||
References |
||||||||
|