Keywords
|
| Disjoint close interval, order pair, probable delay, link weight |
INTRODUCTION
|
| The Constrained Shortest Path problem (CSP) is to identify a minimum cost path from a source node to a destination node whose delay is within specific bound. Communication network is modelled as directed graph with delay parameter associated with each link, We consider the problem of determining most probable delay constrained path [1] from a source node to a destination node. |
| In this paper,Delay of the link is a random variable with known mean and known variance as well as continuous and differentiable probability density function. Using central limit theorem this problem can be formulated as a path problem[2] which involves simultaneously optimizing two additive path parameters by applying constraints on delay bound. It can be considered that the given problem is restricted version of NP-Hard problem which would be treated as NP-Complete problem and has a polynomial solution. |
| Basically, there are two cases arise when there is one path with a mean delay less than delay bound, An exact pseudo polynomial algorithm [1] works. In another case where the path delay meanis greater than the delay bound problem which can be solved in a simple approximation algorithm. Network multimedia applications are becoming increasingly popular and are making a good case for deployment of quality of service (QoS) [3] based Network architecture. One of the key issues in such architecture is how to determine appropriate path that fulfill QoS requirement [4].It is used in applications for video delivery over bandwidth limited networks. Assume that each link in the network has a bandwidth and a delay for a given source-destination pair.According to bandwidth requirement, It is necessary to find a set of source to destination path such that the delay of the longest path is minimized while the aggregated bandwidth from the set of path meets the bandwidth requirement. |
RELATED WORK
|
| The Most probable delay constrained path problem (MPDCP) is related to the traditional multiconstrained QoS routing problem which is known to be NP-Hard. In Paper [1] they made mild assumption on probability distribution of link delay which leads to formulation that requires determining an optimal path with respect to mean path delay and path variance. They considered two cases, one of which requires minimization of both mean path delay and path variance and other require minimization of mean path delay and maximization of path variance. |
| Boston university representative Internet Topology gEnerator(BRITE) [6] is one of the topology generator tool which generates topology in order to provide link weight input as a random variable. Version 1.0 of BRITE requires a Java 2 JDK 1.3. |
PROPOSED ALGORITHM
|
| A. Phasessof Algorithm: |
| The algorithm has three phases (fig 1). In the first phase (Line 1) sort the given disjoint interval in non-decreasing order. In the second phase (Lines 2-8) check whether intervals are disjoint or not. If not made it disjoint by the union of these two intervals. In the third phase(Lines 9-26) complete set of ordering pair [δk , Δk ] Such that K≤mlog(n − 1). |
| B. TERMS USED |
| a) Approximation path:-a probable path whose link delay is maximum |
| b) Disjoint interval:-set of ordered pair that contains lower bound and upper bound. |
| c) Most probable delay path:-gives maximum delay within the link from source to destination. |
| C. PROCESS |
| • Simulate this network using „BRITEâÃâ¬ÃŸ topology. |
| • For all intervals Check whether the interval is disjointor not. |
| • Go to the next interval |
| • Continue this process until all Disjoint interval Covers |
| D.Description of the Proposed Algorithm: |
| Let G be the graph with node n=7 and m=13 according to an algorithm, various observation are listed bellow. maximum set of closed interval J≤m*log (n-1) |
| i.e13log(7-1) = 34 |
| Consider the disjoint intervals are[α1, β1],[a2, β2],[a3, β3],[a4, β4], [a5, β5], [a6, β6]. |
| [1,3], [5,8], [9,16], [18,20], [22,28], [30,32]. |
| On this sorted input proposed algorithm finds set of ordered pair as follows |
 |
 |
PSEUDO CODE
|
| This section presents the designed algorithm which works on how to find out list of ordered pairs by giving a set of disjoint closed interval. |
| Input:- |
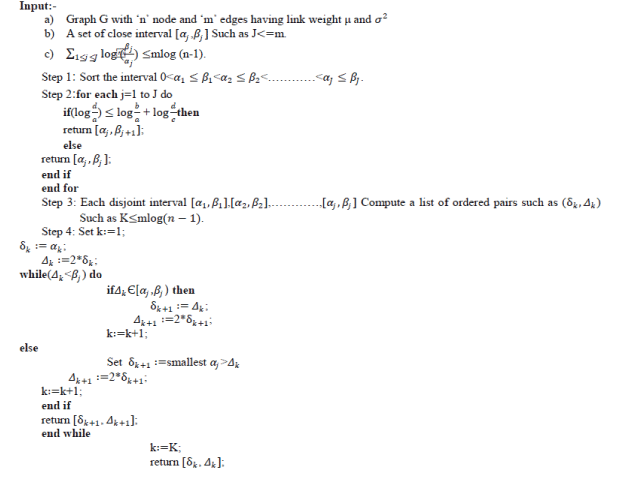 |
SIMULATION RESULTS
|
| Simulation study is carried out using Graph visualization software (Graphviz). Computing most probable delay path between giving graph with certain node and edges.Graphviz layout takes the description of graph in a simple text language and generates a diagrams in an useful format. To run the code in graphviz require special type of extension called as .dot run in linux environment. |
| Dot accepts input in the DOT language. The main (outermost) graph can be directed (digraph) or undirected graph. dot makes layouts of directed graphs as well as undirected graph. (A separate layout utility named as neato [7] draws undirected graphs) In the main graph, a subgraph defines a subset of nodes and edges. A node is created when its name first appears in the file. An edge is created when nodes are joined by the edge operator →. Running dot on this file following is the command. |
| a. $ dot -Tps graph1.dot -o graph1.ps (//dot Tpdf extension filename.dot -o outputfile.pdf extension) |
| b. $ dot -Tjpeg graph1.dot -o graph1.jpeg (//dot Tjpegentension filename.dot –o outputfile.jpeg extension) |
| c. $ dot -Tgif graph1.dot -o graph1.gif (//dot Tgraphics interchange format filename.dot –o outputfile.gif extension) |
| To implement fully polynomial time approximation theorem [1]; requires knowledge of pair of lower and upper bound. For that purpose, following algorithm suggests to compute a set of ordering pair that contains a desired pair (δ,Δ). Let d (i, j) be the random variable associated with the delay of the link (I, j) for path p then d(p)= (Σ(i,jΕp)) d(i, j) And πD(p) = pr[d(p) ≤ D] Where D = Maximum delay requirement. The most probable delay constrained path problem, ask for a path port such that πDopt>=ID(p). |
| The lab experiments were carried out on the linux platform. Table 3 consists of a set of links (m), nodes (n), disjoint closed interval and set of ordered pairs. These set of ordered pair contains one pair that which is desired pair(δ, ïÿýïÿý) and helps to compute most probable delay in polynomial time. |
CONCLUSION AND FUTURE WORK
|
| In this paper, We discuss how to find set of ordered pairs from the disjoint close interval. More importantly, The cardinality of this set is at most mlog(ïÿýïÿý). One of the pair contains tight upper and lower bound which is in a polynomial size. The pair helps us to compute the most probable delay constrained path between given source to destination in the given graph in polynomial time. This work helps us to find most probable delay between given source to destination in polynomial time. This work is helpful to network operator who wants to know about probable factor of bandwidth. The path which belongs to probable maximum delay helps to set amount of delay bound within network. The problem is NP-Hard, however applying constraint on that problem it can solve in polynomial time which reduces computational complexity. |
Tables at a glance
|
|
|
| |
Figures at a glance
|
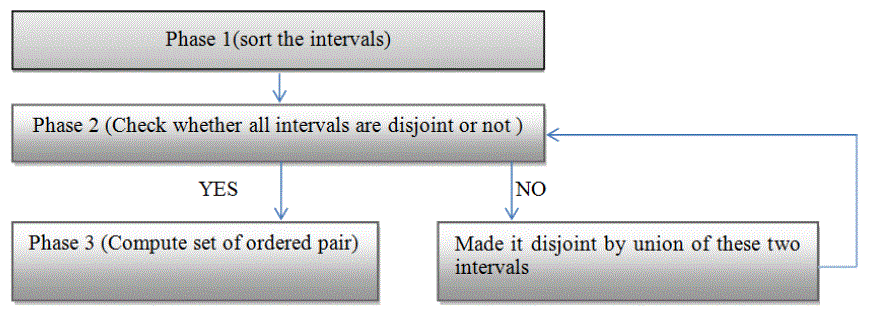 |
| Figure 1 |
|
References
|
- Ying Xiao, KrishnaiyanThulasiraman, Xi Fang, Dejun Yang, and GuoliangXue, “Computing a Most Probable Delay Constrained Path: NPHardnessand Approximation Schemes,” IEEE TRANSACTIONS ON COMPUTERS, VOL. 61, NO. 5 MAY 2012.
- GuoliangXue,Weiyi Zhang, Jian Tang, and KrishnaiyanThulasiraman, “Polynomial Time Approximation Algorithms for Multi-ConstrainedQoS Routing”, IEEE/ACM TRANSACTIONS ON NETWORKING, VOL. 16, NO. 3, JUNE 2008.
- TurgayKorkmaz, and Marwan Krunz, “Bandwidth-Delay Constrained Path Selection Under Inaccurate State Information”, IEEE/ACMTRANSACTIONS ON NETWORKING, VOL. 11, NO. 3, JUNE 2003.
- Ying Xiao, KrishnaiyanThulasiraman, “Approximation and Heuristic Algorithms for Delay Constrained Path Selection under
- Inaccurate State Information”, Proceedings of the First International Conference on Quality of Service in Heterogeneous Wired/WirelessNetworks (QSHINE?04)0-7695-2233-5/2004 IEEE. (Accessed on : Aug 2013).
- Alberto Medina, AnukoolLakhina, Ibrahim Matta, John Byers, “BRITE: An Approach to Universal Topology Generation”, BRITE is
- funded in part by NSF grants CAREER ANI-0096045,CAREER ANI-0093296 and ANI-9986397. (Accessed on : Aug 2013).
- Emden R.Gansner and EleftheriosKoutsofios and Stephen North, "Drawing graphs with dot".( Accessed on :November 2, 2010).
- Alberto Medina, AnukoolLakhina, Ibrahim Matta, John Byers,” BRITE: Universal Topology Generation from a Users Perspective”, BRITE is in part funded by NSF grants CAREER ANI-0096045 and ANI-9986397.( Accessed on :April 12, 2001)
|
| BIOGRAPHY |
| Sujit P. Nale is pursuing his Mtech in Computer Science and engineering. His current research interest includes Theory of Computation. |
| Dr.ShefaliSonavane has completed her M.E Ph.D in Computer Science and engineering and is working as Assistant Professor at department of CSE at WCE Sangli.(MH-India) She is associated with few research projects and has published a good number of papers at National and International leval. Her current research interest includes Theory of Computation and graph theory. |