Keywords
|
| Anonymization and deanonymization cloud and distributed computing systems, multipartycomputation, confidential data mining, confidential protection, security and trust in cooperative communications. |
INTRODUCTION
|
| The popularity of internet as a communication medium whether for personal or business use depends in part on itssupport for anonymous communication. Businesses also have legitimate reasons to engage in anonymouscommunication and avoid the consequences of identity revelation. For example, to allow dissemination of summarydata without revealing the identity key of the entity the underlying data is associated with, or to protect whistleblower’sright to be anonymous and free from political or economic retributions. Cloud-based website managementtools provide capabilities for a server to anonymously capture the visitor’s web actions. The problem of sharingconfidentially held data so that the individuals who are the subjects of the data cannot be identified has been researchedextensively. Researchers have also investigated the relevance of anonymity and/or confidential in various applicationdomains: The associate editor coordinating the review of this patient medical records, electronic voting, e-mail, socialnetworking, etc. Another form of anonymity, as used in secure multiparty computation, allows multiple parties on anetwork to jointly carry out a global computation that depends on data from each party while the data held by eachparty remains unknown to the other parties. A secure computation function widely used in the literature is secure sumthat allows parties to compute the sum of their individual inputs without disclosing the inputs to one another. Thisfunction is popular in data mining applications and also helps characterize the complexities of the secure multipartycomputation. |
| This work deals with efficient algorithms for assigning identifiers (Keys) to the nodes of a network in such a way thatthe Keys are anonymous using a distributed computation with no central authority. Given nodes, this assignment isessentially a permutation of the integers with each Key being known only to the node to which it is assigned. Our mainalgorithm is based on a method for anonymously sharing simple data and results in methods for efficient sharing ofcomplex data. There are many applications that require dynamic unique Keys for network nodes. Such Keys can beused as part of schemes for sharing/dividing communications bandwidth, data storage, and other resourcesanonymously and without conflict. The Keys are needed in sensor networks for security or for administrative tasks requiring reliability, such as configuration and monitoring of individual nodes, and download of binary code or dataaggregation descriptions to these nodes. An application where Keys need to be anonymous is grid computing whereone may seek services without divulging the identity of the service requestor. |
LITERATURE SURVEY
|
| Q. Xie and U. Hengartner proposed an algorithm based upon permutations and substitutions. That algorithmsupports fixed key size approach to secure the data. It is Specification for Advanced encryption standard provides thewhole mechanism for encryption algorithm for which Rijmen provided the concept of AES. It mainly specifies theRijndael algorithm a symmetric block cipher that can process data blocks of 128 bits, by using cipher keys. However,the lengths of Rijndael, which are required to handle additional key lengths and block sizes, are not adopted in thisfollowing standard. |
| This Algorithm provides flexibility to user to choose different key sizes. By using this algorithm throughputincreases with increase in frequency level but the processing time is reduced at high frequency level. In this algorithmround time is the function of processing time so with frequency it also reduces. In this Rijndael provides a securityequivalent to RSA of 3072 bit key and also overcome the drawbacks of DES and TDES. It is also concluded that if thethroughput is increased then the same algorithm can be implemented on optical networks. |
EXISTING SYSTEM
|
| A secure computation function widely used in the literature is secure sum that allows parties to compute the sumof their individual inputs without disclosing the inputs to one another. This function is popular in data miningapplications and also helps characterize the complexities of the secure multiparty computation. Existing and newalgorithms for assigning anonymous IDs are examined with respect to trade-offs between communication andcomputational requirements.. Also, suppose that access to the database is strictly controlled, because data are used forcertain experiments that need to be maintained confidential. Clearly, allowing Alice to directly read the contents of thetuple breaks the privacy of Bob; on the other hand, the confidentiality of the database managed by Alice is violatedonce Bob has access to the contents of the database. Thus, the problem is to check whether the database inserted withthe tuple is still k-anonymous, without letting Alice and Bob know the contents of the tuple and the databaserespectively. |
DISADVANTAGES OF EXISTING SYSTEM
|
| The algorithms for mental poker are more complex and utilize cryptographic methods as players must, ingeneral, be able to prove that they held the winning hand. Throughout this paper, we assume that the participants aresemi-honest, also known as passive or honest-but-curious, and execute their required protocols faithfully. Given asemi-honest, reliable, and trusted third party, a permutation can also be created using an anonymous routing protocoland The database with the tuple data does not be maintained confidentially. |
PROPOSED SYSTEM
|
| This work deals with efficient algorithms for assigning key identifiers (keys) to the nodes of a network insuch a way that the Keys are anonymous using a distributed computation with no central authority. Given N nodes,this assignment is essentially a permutation of the integers {1,…..N} with each key being known only to the node towhich it is assigned. Our main algorithm is based on a method for anonymously sharing simple data and results inmethods for efficient sharing of complicated data. Despite the differences cited, the reader should consult and considerthe alternative algorithms mentioned above before implementing the algorithms in this paper. This paper builds analgorithm for sharing simple integer data on top of secure sum. The sharing algorithm will be used at eachiteration of the algorithm for anonymous Key assignment (AKA). This AKA algorithm, and the variants that wediscuss, can require a variable and unbounded number of iterations. The work reported in this paper further explores theconnection between sharing secrets in an anonymous manner, distributed secure multiparty computation andanonymous Key assignment. The use of the term “anonymous” here differs from its meaning in research dealingwith symmetry breaking and leader election in anonymous networks. Our network is not anonymous and the participants are identifiable in that they are known to and can be addressed by the others. Methods for assigning andusing sets of pseudonyms have been developed for anonymous communication in mobile networks. The methodsdeveloped in these works generally require a trusted administrator, as written, and their end products generallydiffer from ours in form and/or in statistical properties. |
ADVANTAGES OF PROPOSED SYSTEM
|
| Increasing a parameter in the algorithm will reduce the number of expected rounds. However, our central algorithmrequires solving a polynomial with coefficients taken from a finite field of integers modulo a prime. That task restrictsthe level to which can be practically raised. We show in detail how to obtain the average number of required rounds,and in the Appendix detail a method for solving the polynomial, which can be distributed among the participants. |
| Modules: |
| 1. Homomorphic encryption Module |
| 2. Generalization Module |
| 3. Cryptography Module |
| 4. User and Admin Module |
| 1. Homomorphic encryption Module: |
| This module to use the first protocol is aimed at suppression-based anonymous databases, and it allows the ownerof DB to properly anonymize the tuple t, without gaining any useful knowledge on its contents and without having tosend to it’s owner newly generated data. To achieve such goal, the parties secure their messages by encrypting them. Inorder to perform the privacy-preserving verification of the database anonymity upon the insertion, the parties use acommutative and homomorphic encryption scheme. |
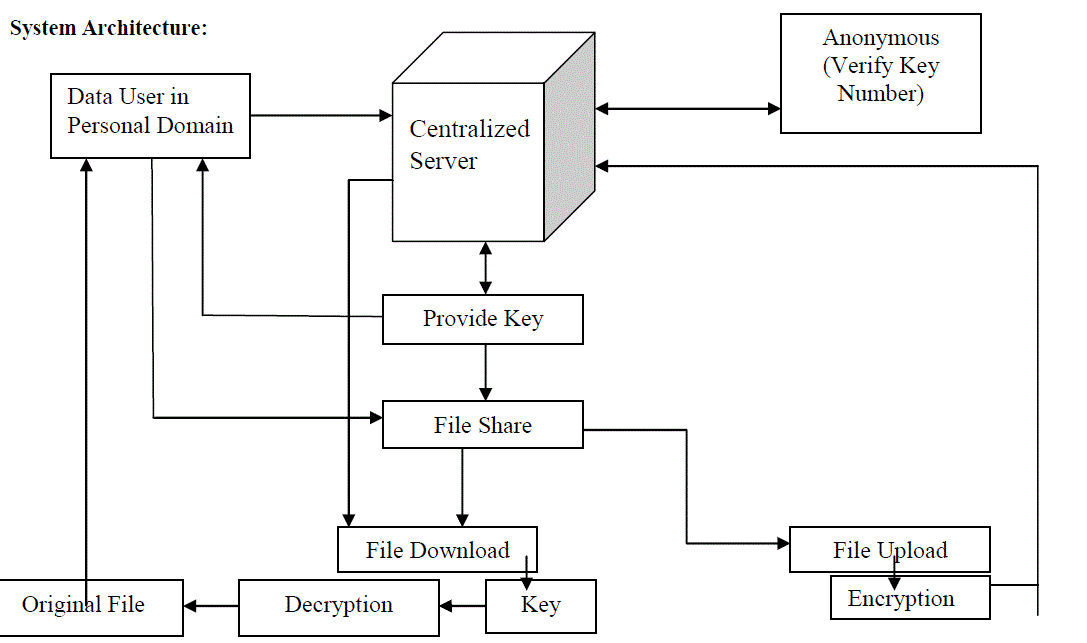
| System Architecture: |
| 2. Generalization Module: |
| In this module, the second protocol is aimed at generalization-based anonymous databases, and it relies on a secureset intersection protocol, such as the one found in, to support privacy-preserving updates on a generalization based kanonymousDB. |
| 3. Cryptography Module: |
| In this module, the process of converting ordinary information called plaintext into unintelligible gibberish calledcipher text. Decryption is the reverse, in other words, moving from the unintelligible cipher text back to plaintext. Acipher (or) cypher is a pair of algorithms that create the encryption and the reversing decryption. The detailed operationof a cipher is controlled both by the algorithm and in each instance by a key. This is a secret parameter (ideally knownonly to the communicants) for a specific message exchange context. |
| 4. User and Admin Module: |
| In this module, to arrange the database based on the patient and doctor details are recorded. The admin encrypts thepatient reports using encryption techniques using suppression and generalization protocols. |
| Fig 1 Shows the System Architecture for Confidential Data Sharing in Cloud. When the data user in the personaldomain wants to access the information he can make use of key provided by the centralized server. The user uses thatkey to decrypt the data. There is an anonymous user which verifies the key generated by the server. User can downloadthe file that is uploaded by the other user and he can easily decrypt the data using the key provided by the server. File isuploaded to the server in the encrypted form. No other user can see the contents of file or he will not be able todownload that file. After decryption user gets the original file. |
RELATED WORK
|
| To differentiate anonymous key assignment from anonymous communication, consider a situation where parties wishto display their data collectively, but anonymously, in slots on a third party site. The Keys can be used to assign theslots to users, while anonymous communication can allow the parties to conceal their identities from the third party. Inanother application, it is possible to use secure sum to allow one to opt-out of a computation beforehand on the basis ofcertain rules in statistical disclosure limitation or during a computation and even to do so in an anonymous manner.However, very little is known with respect to methods allowing agencies to opt-out of a secure computation based onthe results of the analysis, should they feel that those results are too in for- motive about their data. The work reportedin this paper further explores the con- section between sharing secrets in an anonymous manner, distributed securemultiparty computation and anonymous key assignment. The use of the term “anonymous” here differs from itsmeaning in research dealing with symmetry breaking and leader election in anonymous networks. Our network is notanonymous and the participants are identifiable in that they are known to and can be addressed by the others. Methodsfor assigning and using sets of pseudonyms have been developed for anonymous communication in mobile net- works .The methods developed in these works generally require a trusted administrator, as written, and their end productsgenerally differ from ours in form and/or in statistical properties. To be precise, with nodes the algorithms of this paperdistribute a computation among the nodes generating a permutation of chosen with a uniform probability of from theset of all permutations of where will know only. Such a permutation can also be produced by algorithms designed formental poker. The algorithms for mental poker are more complex and utilize cryptographic methods as players must, ingeneral, be able to prove that they held the winning hand. Throughout this paper, we assume that the participants aresemi honest also known as passive or honest-but-curious, and execute their required protocols faithfully. Given a semihonest, reliable, and trusted third party, a permutation can also be created using an anonymous routing protocol.Despite the differences cited, the reader should consult and consider the alternative algorithms mentioned above beforeimplementing the algorithms in this paper. This paper builds an algorithm for sharing simple integer data on top ofsecure sum. The sharing algorithm will be used at each iteration of the algorithm for anonymous Key assignment(AKA). This AKA algorithm and the variants that we discuss, can require a variable and unbounded number ofiterations. Finitely-bounded algorithms for AKA are discussed in Section IX. Increasing a parameter in the algorithmwill reduce the number of expected rounds. However, our central algorithm requires solving a polynomial withcoefficients taken from a finite field of in tegers modulo a prime. That task restricts the level to which can be practicallyraised. We show in detail how to obtain the average number of required rounds, and in the Appendix detail a methodfor solving the polynomial, which can be distributed among the participants |
A SECURE SUM OF DATA ALGORITHM
|
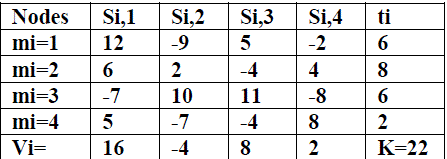
| Given nodes m1…….mN each holding a data item ti from a finitely represent able abelian group, allocate the value K =Σti between the nodes without revealing the values ti. Each node mi, i = 1 …N selects random values si,1………si,Nsuch that si1,+…..+si,N= ti. Each random value si,j is conveyed from node mi to node mj . The sum of all these randomnumbers si,j, is the desired total K. Each node mj totals all the random values received as vj = s1,j+…..+sN,j. Eachnode mi merely broadcasts vi to all other nodes so that each node can compute: K = v1 +…..+vN. In the given Fig 2,the initial data items held by nodes m1, m2, m3 and m4 are t1=6, t2= 8, t3=6, t4=2 correspondingly. Node m2 wouldtransmit 6, 2, -4, and 4 to nodes m1, m2, m3 and m4 respectively. Node m2 would receive -9, 2, 10, and -7 from nodesm1, m2, m3 and m4 respectively. Then node m2 would work out and broadcast the total v2 = -4 of the values receivedto all nodes. Finally, m2 would compute the total of all the second round transmissions received 22=16+-4+8+2.The opportunity that more complicated data is to be shared among the participating nodes is to be considered. Eachnode mi has a data item ti of length u-bits which it wishes to put together it public anonymously to other participants.As the number of nodes and the bits per data item becomes larger, to accomplish this sharing, an indexing of the nodeswas utilized as an alternative. Considering that each node mi has a unique identification number vi ? {1, 2…..N} and additionally, assume that no node has knowledge of the unique identification number vi of any other node, and thatv1…..vN are a random permutation of 1,…N ., and is termed an Anonymous Key Assignment and may possibly beused to allocate slots with reverence to time or space for storage or communications It may be promising to minimallyhave a database by means of central storage locations Ei such that each node merely stores its data there setting Evi:=ti. A simple algorithm was presented for finding an AKA which has quite a few variants depending on the selectionof the data sharing method. Random integers or slots between 1 and P are chosen by each node at one step. Theposition of the node will be determined by means of its position among the selected slots; however provisions must beprepared for collisions. The parameter should be selected so that P ≥N. The technique of confidential data sharing ofAnonymous Data Sharing with Power Sums is challenging to the collusion of any subset of the participating nodeswhile based on the secure sum Algorithm. For the reason that the input data is present as a multi set in the output ofeach party and all parties are semi-honest the consequence is implied by the secure sum Algorithm. The data sharing isanonymous in the intellect that the sources of the data items cannot be traced. Certainly, it is potential that a given datavalue would make logic only for a definite participant due to several factors such as the participants relative sizes. |
THE ALGORITHM TO FIND AN AKA
|
| In this algorithm It requires the random numbers be shared anonymously and we consider three methods which arevariants of that procedure and require the parameter P in each case. The expected numbers of rounds rely simply on theselection of P and not on the variant selected. In the slot selection method the variant of the algorithm has its mainnegative aspect as the very long message lengths that are encountered while using large P to maintain the number ofexpected rounds small. In the Prime Modulus AKA: A prime R > P is chosen. In general, R will be chosen as small aspotential subject to this restriction. This variant will be seen to outcome in shorter message lengths intended forcommunication among nodes. Again, the computation necessary to find the roots of the Newton polynomial can bedelayed and consequently overlaps any supplementary required rounds. It is probable to keep away from solution of theNewton polynomial completely. Sturm’s theorem permits the determination of the number of roots of a real polynomialq(x) in an interval (g, h) based on the signs of the values of a sequence of polynomials derived from q(x). Thesuccession of polynomials is attained from a variant of the Euclidean Algorithm. By means of Sturm’s theorem is not at Present reasonable with the variety of methods of polynomial solution using the prime modulus method and runs twiceas slow at best. The application of Sturm’s theorem necessitates usage of an ordered field resulting in large polynomialcoefficients. |
PROPOSED ALGORITHM
|
| This paper builds an algorithm for sharing simple integer data on top of secure sum. The sharing algorithm will be usedat each iteration of the algorithm for anonymous Key assignment (AKA). This AKA algorithm, and the variants that wediscuss, can require a variable and unbounded number of iterations. Increasing a parameter in the algorithm will reducethe number of expected rounds. However, our central algorithm requires solving a polynomial with coefficients takenfrom a finite field of integers modulo a prime. That task restricts the level to which can be practically raised. |
Sturm’s Theorem
|
| The usage of secure multiparty computation is being avoided with the usage of Sturm’s theorem to make sure that theinformation about the nodes are not revealed. In the current system the main goal is to provide anonymous key for eachnode. Each node will have a secure communication of simple and complicated data. Those data’s may be from staticdata or dynamic data. By implementing secure sum hides permutations method and anonymous key assignment (AKA)method the permutation methods are kept anonymous to each other |
Sturm’s Theorem AKA
|
| It is possible to avoid solution of the Newton polynomial entirely. Sturm’s theorem allows the determination of thenumber of roots of a real polynomial p(x) in an interval (a, b) based on the signs of the values of a sequence ofpolynomials derived from p(x). The sequence of polynomials is obtained from a variant of the Euclidean Algorithm. Asin the previous variant, the power sums are collected and the Newton Polynomial is formed. However, the field usedfor computation is the field of rational numbers Q. The test p′(ri)=0 is again sufficient to determine whether or not nihas received. There is a computational advantage which is arises in that nodes which do not need to solve the Newtonpolynomial p(x) to determine the (now implicitly) shared values. Assume that x=0 is not a root of p(x) as xk has beenfactored out immediately if applicable. Each node ni which has received an assignment must count separately multipleroots and also forms g(x)=gcd(p(x), p′(x)). A multiple roots version of Sturm’s theorem is then applied to calculate thenumber of roots for the polynomial p(x) in the range (0,ri). (Note that ri itself is not a multiple root allowing applicationof the theorem). The polynomial g(x)=gcd(p(x),p′(x)) is a byproduct of this computation. The same Sturm procedure isapplied to g(x) thus obtaining a count of the multiple roots in the same range,(0,ri). The collected power sums Pi areintegers. To guarantee the privacy and the compute sums using a field GF (P) with P greater than any possible value ofPi. Our timings showed that using Sturm’s theorem is not currently competitive with the various methods ofpolynomial solution using the “prime modulus” approach and runs twice as slow as best. Although, the construction isstraight forward. The application of Sturm’s theorem requires the use of an ordered field resulting in the largepolynomial coefficients. Unfortunately, the analog of this result which is usable for a finite field of the correspondingpolynomial coefficient. Still, some results in this direction are available. |
CONCLUSION AND FUTURE WORK
|
| The required computations are distributed without using a trusted central authority. Any person can be use privatecommunication channel then access the database. The algorithms for assigning the anonymous key is examined by thetrade-offs between the requirements of communication and computations. The new algorithms are built on top of asecure sum data mining operation using Newton’s identities and Sturm’s theorem. An algorithm for the distributedsolution of certain polynomials over finite field will enhances the scalability of the algorithms. |
Figures at a glance
|
 |
 |
| Figure 1 |
Figure 2 |
|
References
|
- Alipio BC, David FC, Isabel RS, Juan CNM. Manuel AE. Comparison of batch, stirred flow chamber, and column experiments to study adsorption, Desorption and transport of carbofuran within two acidic soils. Chemosphere. 2012; 88(1): 106-120.
- Arnaud B, Richard C, Michel S. A comparison of five pesticides adsorption and Desorption processes in thirteen contrasting field soils. Chemosphere. 2005; 61(5): 668-676.
- Chunxian W, Jin-Jun W, Su-Zhi Z, Zhong-Ming Z. Adsorption and Desorption of Methiopyrsulfuron in Soils. Pedosphere. 2011; 21(3): 380-388.
- Chunxian W, Suzhi Z, Guo N, Zhongming Z, Jinjun W. Adsorption and Desorption of herbicide monosulfuron-ester in Chinese soils. J Environ Sci. 2011; 23(9): 1524-1532.
- Christine MFB, Josette MF. Adsorption-desorption and leaching of phenylurea herbicides on soils. Talanta. 1996; 43(10): 1793-1802.
|
| BIOGRAPHY |
| Mr. P. B. More is an Assistant Professor in the Computer Science and Engineering/Information Technology Department of Adarsh Institute of Technology and Research Center, Vita. Shivaji University, Kolhapur (Maharashtra), India. He received Master of Technology (M .Tech) degree in the year 2015 from JNTU, Hyderabad, India |
| Mr. Y. B. Amane is an Assistant Professor in the Computer Science and Engineering/Information Technology Department of Adarsh Institute of Technology and Research Center, Vita. Shivaji University, Kolhapur (Maharashtra), India He received Master of Technology (M .Tech) degree in the year 2013 from JNTU, Hyderabad, India. |