Cooperative Communication over Rayleigh
Fading Channel

Vijayan T

Cooperative Communication over Rayleigh Fading Channel

Vijayan T
Asst. Professor, Dept of E&I, Bharath University, Chennai-600073, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

It is a new way of combating the effect of signal fading. The main goal of this communication is to maximize throughput and to improve spectral efficiency. The main aim is to minimize the bit error rate (BER) for Cooperative Communication systems with hierarchical modulation over additive white Gaussian noise (AWGN) and Rayleigh fading channel. The error rate performances can be analyzed by each of the transmission bits. a criterion is proposed to choose the optimal distance parameters for minimizing the BER of the refinement bits while guaranteeing the BER requirement of the base bits. Simulation results validate the correctness of the derived BERs of the base bits and the refinement bits.

INDEX TERMS

Hierarchical modulation, cooperative communication, BER analysis, AWGN, and Rayleigh fading.

INTRODUCTION

MULTIMEDIA is an integration of different content formats in a way that provides individual users with interactions. Owing to the properties of the real-time fashion for such interactions, having sufficient bandwidth and providing good quality of services (QoS) are needed. However, wireless environment is variant and the transmitted signal is often faded, which make the job of delivering multimedia messages with QoS through wireless environment hard to fulfill. To overcome this, cooperative communication [1]–[5] opens a new concept for the diversity technique to exploit the potential of broadcasting nature and thereby achieve tremendous improvements in spectral efficiency. Those cooperative systems mainly employ the traditional modulation strategies with the goal to maximize the throughput. However, this goal cannot guarantee the QoS for multimedia due to the variation of channel condition. Thus, using conventional modulation schemes to carry multimedia messages would be no longer satisfactory. To this end, many literatures [6]–[12] had devoted their attentions to hierarchical modulation because of its capability of offering different levels of protections to transmitted signals according to their significance. Wang and et.al. [13] first adopted the hierarchical modulation in the cooperative communication systems and proposed a new cooperation strategy of how relays forward the received signals. However, they dealt with one-dimensional hierarchical modulation and assumed the same constellation at each relay for all relays adopts the same distances of the constellation points. In this work, we deal with two-dimensional hierarchical modulation and assume that the constellations of the relay and source can be different.

In cooperative system, the relay nodes can help the source to improve the performance at the destination. This is under the condition that the relay nodes can perfectly demodulate the received signal from the source. However, when the detection errors occur at the relay node, then the relay node will forward the wrong information to the destination and cause the error propagation. In this work, we take this fact into account and derive the BER performance when the hierarchical modulation is adopted in the cooperative communication systems. We first analyze the bit error rates of both base bits and refinement bits under the assumption that the constellations of the relay and the source are different. The difference in the constellations makes the system more flexible and we can manipulate this difference to improve the system performance. In order to take every possible detection error into consideration, we discuss the relationship of the distance parameters of hierarchical modulation between the source and the relay nodes. Based on this knowledge, a criterion is proposed to choose proper distance parameters for minimizing the BER of the refinement bits while fulfilling the BER requirement of the base bits. Through extensive simulation, we demonstrate the correctness of the closed-form expression for BER and the workability of the proposed criterion to select suitable distance parameters.

SYSTEM MODEL

In this system, we employ 4/16-QAM hierarchical modulation with Gray code mapping in cooperative communication system over independent Rayleigh fading channels. Within this network, only one relay employing demodulate-and-forward protocol with two-phase transmission helps source’s transmission. The block diagram for our system is depicted in Fig.1.The multimedia stream u in the source node is classified into two subsets, Cb and Cr, in terms of their significance. Cb and Cr are the base bits and the refinement bits, respectively. In phase 1, Cb and Cr are embedded within a symbol x s broadcasting to the relay and the destination with energy s a E . In phase 2, the relaydemodulates the received symbol from the source node and then forwards this demodulated symbol x’ s with energy E r a , to destination.

Let h s,d , hs,,r,, hr,d be the zero-mean complex Gaussian gains between the source and the destination, the source and the relay nodes and the relay node and the destination, respectively and let σs,d, σs,r and σr,d be the respective variances of these three random variables. Let ns,d, ns,r, nr,d be the zero-mean complex Gaussian noises with variance of N0 between the source and the destination, the source and the relay node and the relay node and the destination, respectively. The received signals at the relay and the destination during the phase 1 are

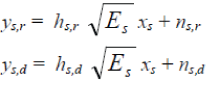respectively, where Es is the transmitted energy of the source. During the phase 2, the received signal at the destination from the relay is

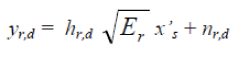where Er is the transmitted energy of the relay and x’s is the transmitted symbol of the relay. Upon receiving the signals from the source and the relay node, the destination coherently combines both signals using Maximal ratio combining (MRC) method. Thus, the combined signal is given by

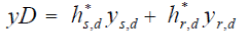in which ys,d and yr,d are the received signals from the source and the relay node, respectively.

A. The Distance Parameters for Hierarchical Modulation

Based on 4/16-QAM hierarchical modulation with Gray code mapping [11], the constellation shown in Fig. 2 can be viewed as the combination of two quadrature phase shift keying (QPSK) modulations. In this fashion, the base bits can be viewed as one of the fictitious QPSK symbols, whereas the refinement bits can be viewed as one of the another fictitious QPSK symbols surrounding the fictitious QPSK symbol of the base bits. As for the distance parameters of constellation pattern, the distance between two fictitious symbols of the base bits is 2d1,s, and the distance between two neighboring symbols within the same quadrant is 2d2,s for the source.

Similarly, the relationship between distance parameters and the energy for the relay node can be obtained.

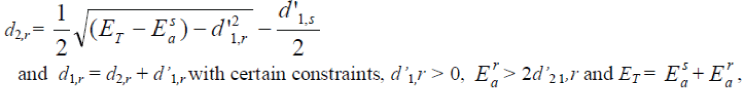where ET is the total energy of each transmission. In this work, we allow the distance parameters of the source and the relay nodes are different from each other. This difference gives the system the freedom to choose the preferable distance parameters to improve or maintain the system performance.

PERFORMANCE ANALYSIS

The performance analysis of the point-to-point transmission with hierarchical modulation had been investigated by many papers. Reference [11] and [12] had obtained the exact expression for the BER of the 4/16-QAM constellations over AWGN channel and the leading-term approximation of BER for the case of Rayleigh fading. In this work, we extend their analyses of error rate performance to the case of the cooperation system over Rayleigh fading channels and AWGN channels. To accomplish this job, a proposed analyzing model is used to enumerate all transmission possibilities for clarity. By means of this model, the exact error performance depending on constellation parameters, which control the relative message importance, could be expressed.

A. Analyzing Model

To find the BERs for the base bits and the refinement bits and the symbol error rate (SER) for the cooperative system. By utilizing the symmetric feature of the I-channel and the Q-channel, the original two dimensional analysis is reduced to a one-dimension analysis. For simplicity and clarity, an analyzing model shown in Fig. 3 is introduced to illustrate all possible situations when the possible transmitting symbols at the source are 1_0_ and 1_1_ in which X_Y _ means the bits of the base information and the refinement information on I-channel are X and Y , respectively.

In this model, there are four steps to complete the procedure of error rate analysis. By means of defining each state and finding the transition probabilities between states, the average BER and SER could be obtained accordingly. To begin with, we define the states in each step. In STEP 1, we consider the two possible transmitting symbols at the source, 1_0_ and 1_1_,which are defined as state 11 and 12, respectively. Due to the symmetry, the analysis of the case of 0_0_ and 0_1_ is the same as that of 1_0_ and 1_1_. Thus, we only focus on the case of 1_0_ and 1_1_ and apply the result to the case of 0_0_ and 0_1_. In STEP 2, based on the transmitted symbol given in STEP 1, there are four possible symbol candidates, 1_0_, 1_1_, 0_1_ and 0_0_, at the relay node depending on the result of demodulation, which correspond to state 2i, for i = 1, 2, 3, 4, respectively, as shown in Fig. 3. In STEP 3, according to the transmitted symbol in STEP 1 and the relayed symbol in STEP 2, there are also four possible symbol candidates at the destination node, which correspond to state 3i, for i = 1, 2, 3, 4. Finally, in STEP 4, the state B and state R denote the occurrence of errors in the base bits and the refinement bits respectively. According to the traversed path from STEP 1 to STEP 4, the BER of the base bits and the refinement bits can be evaluated. In turns, we define the transition probability from the state 1i to the state 2j as P1i→2j|1i, for i = 1, 2 and j = 1, 2, 3, 4. Due to the event in STEP 3 is related to the events in STEP 1 and 2, the transition probability from STEP 2 to 3 should be treated as a conditional one and notated as P2j→3k|1i→2j, for k = 1, 2, 3, 4. Based on the proposed analyzing model, we define the conditional BER of the base bits and the refinement bits associated with the history of traversed path as

where δab is 1 if a = b and is 0 otherwise. It is worthwhile to note that Pe,b|1i→2j→3k and Pe,r|1i→2j→3k are either 1 or 0 depending on the traversed path.

Based on this analyzing model, we can obtain the conditional BER and then the average BER for the base bits and the refinement bits can be written as

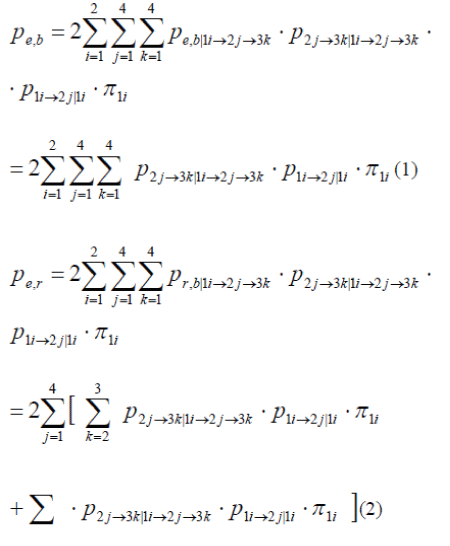Note that due to the symmetry, the analysis of the case of 0_0_ and 0_1_ is the same as that of 1_0_ and 1_1_. Therefore, a factor of 2 is put in front of the right hand sides of Pe,b and Pe,r. Finally, the SER can be expressed as

In AWGN case, let all the fading gains to be 1 and obtain the corresponding BER for the base bits and the refinement bits as well as SER.

CRITERION OF CHOOSING PROPER DISTANCE PARAMETERS

For multimedia transmission, the basic requirement of message delivery in wireless environment is to provide a consistent quality of service. To provide a consistent quality of service, it is required that the error rate of the base bits can meet a certain requirement. To further improve the quality of service, we can resort to improve the error rate of the refinement bits. To accomplish this target, based on the results of the error rate performance, a criterion is proposed to find the optimal distance parameters for minimizing the BER of the refinement bits while the BER requirement of the base bits can be met.

First, let the minimum error probability and the target error probability of the base bits be P ^min_e,b and P ^target_e,b respectively. P ^min_e,b is the minimum achievable BER probability under a certain total energy constraint and is obtained numerically. Since the error probability of the refinement bits is a function of d’1,s and d’1,r, we can denote it as Pe,r(d’1,s, d’1,r). To achieve the aforementioned goal, the proper distance parameters can be selected by solving the following optimization problem:

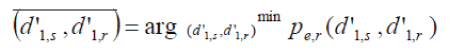By adopting this criterion, we are able to find the optimal distance parameters to fulfill the BER requirement of the base bits and minimize the BER performance of the refinement bits at the same time. It is worthwhile to note that this optimization problem is a nonlinear programming. In this work, we adopt the augmented Lagrangian method to solve this problem and its details can be found in [14], which are omitted due to the length constraint.

The main point we would like to make is the cooperative communication can give system designer more freedom to choose the system-wise parameters to meet the diverse needs of users. When using hierarchical modulation in traditional point-to point communication environment, the adjustment parameters has limited impact on the overall performance. Compared to that, in cooperative communication environment, by changing the distance parameters of both the source and the relay node simultaneously, we are able to easily obtain the desired performance and fulfill the needs of difference services.

SIMULATION RESULTS

In this section, we numerically evaluate the performance of the cooperation communication system when the hierarchical modulation is adopted. To compare the effect of distance parameters, we plot the BER performances of the base bits and the refinement bits as a function of ET /N0 under different d’1,s when the total transmission energy ET is kept constant. Fig. 4 shows the results for d’1,s = 1.2, d’ 1,s = 1.4 and d’1,s = 1.9 when s Ea = 8 and d’1,r = 0.0001 over Rayleigh fading channel. Purple lines, red lines and blue lines represent the case of d1,s = 1.2, the case of d’1,s = 1.4 and the case of d’1,s = 1.9 respectively. The case of d’1,s = 1.9 has better BER performance of the base bits compared to that of the cases of d’1,s = 1.4 and d’1,s = 1.2. However the BER performance of the refinement bits. These results clearly point out the effect of the adjustment of distance parameters. The larger d’1,s provides a greater protection for the base bits at the expense of the refinement bits. Particularly, when the smaller d’ 1,s is used in the case of Rayleigh fading, the error performance of the refinement bits is better than that of the base bits since ET /N0 is over 24 dB. These results imply the depending on the need of BER of the base bits or the need of BER of the refinement bits, there exists an optimal distance parameters. Thus, these results motivate us to propose the criterion in the previous section. Also from Fig. 4, the discrepancies between the simulation results and the theoretical results for both the base bits and the refinement bits are small. This confirms the correctness of our performance analysis.

In Fig. 5, we show the effect of the relay on the performance of the base bits and the refinement bits when the constellation of the source is kept the same. This figure shows the correctness of the performance analysis in this work. Also from Fig. 5, we can see that when d’1,r is getting smaller, the performance of the base bits gets worse and that of the refinement bits gets better. This tells that the relay can help improve the performance of the refinement bits at the expense of the base bits. This tradeoff again motivates us to propose a strategy of selecting suitable d’1,s and d’1,r to satisfy the performance requirement of the system.

Fig. 6 is presented to show the improvement of BER performance of the refinement bits over and Rayleigh fading channels due to the proposed selection criterion for the distance parameters. Here we let P ^target_e,b , = 10−2. When Ea = 8, the BER of the refinement bits with optimal distance parameters is greatly improved compared with the non-optimal cases in Fig. 4 and 5.With the increment of s Ea , we can see the substantial improvement in the performance of the refinement bits. Thus, compared to the traditional point-to-point communication, adopting the cooperative communication gives us more freedom to adjust the distance parameters at the source and the relay node and to fulfill the needs of the different requested services.

CONCLUSION

In this work, we have derived the performance of 4/16 QAM hierarchical modulation with Gray code mapping in cooperative communication system over independent Rayleigh fading channels. Based on this analysis, we have proposed an approach to select distance parameters in the source and the relay. The proposed approach has shown to be able to improve the BER of the refinement bits while maintaining the BER of the base bits. This also shows the flexibility of the cooperative communication systems over the conventional systems.

Figures at a glance


Figure 1	Figure 2	Figure 3


Figure 4	Figure 5	Figure 6

References

A. K. Sadek, Z. Han, and K. J. R. Liu, “An efficient cooperation protocol to extend coverage area in cellular networks," in Proc. IEEE WCNC, 2006, pp. 1687-1692.
Z. Han and H. V. Poor, “Lifetime improvement of wireless sensor networks by collaborative beam forming and cooperative transmission," in Proc. IEEE ICC, June 2007, pp. 3954-3958.
E. Yazdian and M. R. Pakravan, “Adaptive modulation technique for cooperative diversity in wireless fading channel," in Proc. IEEE PIMRC, Sept. 2006, pp. 1-5.
E. C. Strinati, S. Yang, and J. C. Belfiore, “Adaptive modulation and coding for hybrid cooperative networks," in Proc. IEEE ICC, June 2007, pp. 4191-4195.
M. O. Hasna, “On the capacity of cooperative diversity systems with adaptive modulation," in Proc. IEEE WOCN, Mar. 2005, pp. 432-436.
K. Ramchandran, A. Ortega, K. M. Uz, and M. Vetterli, “Multiresoluton broadcast for digital HDTV using joint source/channel coding," IEEE J. Select. Areas Commun., vol. 11, pp. 6-23, Jan. 1993.
M. Morimoto, M. Okada, and S. Komaki, “A hierarchical image transmission system in a fading channel," in Proc. IEEE ICUPC, Nov. 1995, pp. 769-772.
M. B. Pursley and J. M. Shea, “Adaptive nonuniform phase-shift-key modulation for multimedia traffic in wireless networks," IEEE J. Select. Areas Commun., vol. 18, pp. 1349-1407, Aug. 2000.