ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| Vinit Pereira 1, NajibGhatte2, MadurDattaprasad3, TusharSurwadkar4 PG Student [Electronics], Dept. of Electronics, Fr. Conceicao Rodrigues College of Engg.,Bandra, Mumbai, India 1,2,3,4 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
CRC refers to cyclic redundancy check bits used for error detection purpose. Normally the frame format consists of data bits combined with CRC bits which results in packet transmission from source to destination. Teracopy is one of the important application where CRC calculation is done. Due to some reasons it may happen that data transmitted from the source to destination gets corrupted and arrives with error at the receiving end. Now, the CRC bits play very important role for finding out the error in the received packet. For n length of the data if n errors occur then all the errors can be detected. CRC calculation is based on the division method which is very simple for detection of multiple errors. It even gives the position of bit or bits which are toggled at the receiver with respect to the transmitter. Standard polynomials used for CRC calculation are applicable for 1 to n bits of data.
Keywords |
||||||||
| CRC polynomials, Division method | ||||||||
INTRODUCTION |
||||||||
| A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to raw data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents; on retrieval the calculation is repeated, and corrective action can be taken against presumed data corruption if the check values do not match. CRCs are so called because the check (data verification) value is a redundancy (it adds no information to the message) and the algorithm is based on cyclic codes. CRCs are popular because they are simple to implement in binary hardware, easy to analyze mathematically, and particularly good at detecting common errors caused by noise in transmission channels. Because the check value has a fixed length, the function that generates it is occasionally used as a hash function. The CRC was invented by W. Wesley Peterson in 1961; the 32-bit polynomial used in the CRC function of Ethernet and many other standards is the work of several researchers and was published during 1975.[1] | ||||||||
| Cyclic redundancy codes (also known sometimes as cyclic redundancy checks) have a long history of use for error detection in computing. [Peterson72] and [Lin83] are among the commonly cited standard reference works for CRCs. A treatment more accessible to non-specialists can be found in [Wells99]. A CRC can be thought of as a (non-secure) digest function for a data word that can be used to detect data corruption. Mathematically, a CRC can be described as treating a binary data word as a polynomial over GF(2) (i.e., with each polynomial coefficient being zero or one) and performing polynomial division by a generator polynomial G(x). The generator polynomial will be called a CRC polynomial for short. (CRC polynomials are also known as feedback polynomials, in reference to the feedback taps of hardware-based shift register implementations.) The remainder of that division operation provides an error detection value that is sent as a Frame Check Sequence (FCS) within a network message or stored as a data integrity check. Whether implemented in hardware or software, the CRC computation takes the form of a bitwise convolution of a data word against a binary version of the CRC polynomial. Error detection is performed by comparing an FCS computed on a piece of retrieved or received data against the FCS value originally computed and either sent or stored with the original data. An error is declared to have occurred if the stored FCS and computed FCS values are not equal. However, as with all digital signature schemes, there is a small, but finite, probability that a data corruption that inverts a sufficient number of bits in just the right pattern will occur and lead to an undetectable error. The minimum number of bit inversions required to achieve such undetected errors (i.e., the HD value) is a central issue in the design of CRC polynomials. The essence of implementing a good CRC-based error detection scheme is picking the right polynomial. The prime factorization of the generator polynomial brings with it certain potential characteristics, and in particular gives a trade-off between maximum number of possible detected errors vs. data word length for which the polynomial is effective. Many polynomials are good for short words but poor at long words, and the converse. There are relatively few polynomials that are excellent for medium-length data words while still being good for relatively long data words.[2] | ||||||||
DESIGN |
||||||||
| The Cyclic Redundancy Check (CRC) is an efficient technique for detecting errors during digital data transmissions between a source and a destination. The destination device calculates the CRC of the received data. If the CRC calculated by the destination device does not match the one calculated by the source device, then the received data contains an error. This technique is used in a wide variety of applications from Ethernet transmission to daily file transfers. It provides quick and easy insurance of data integrity within digital communication systems The CRC is based on polynomial manipulations which treat each received message as a binary number. The received message is then divided by a fixed value, also known as the generator polynomial, using modulo-2 arithmetic. The characteristic of the CRC implementation is determined by the generator polynomial selection. The generator polynomials are selected to maximize the error detection capability without using too many resources. Generator polynomials that have been incorporated into standards such as CRC-8, CRC-16 and CRC-CCIT are commonly known and are well tested. This reference design describes the use of Lattice programmable devices to implement the CRC generator and checker. The design allows users to implement the CRC using different generator polynomials.[ | ||||||||
| A way of viewing the CRC process is to express all values as polynomials in a dummy variable X, with binary coefficients. The coefficients correspond to the bits in the binary number. Thus, for M = 110011, = 5 + =4 + + 1, and, for P = 11001, = 4 + 3 + 1. Arithmetic operations are modulo 2. The CRC process can now be described as | ||||||||
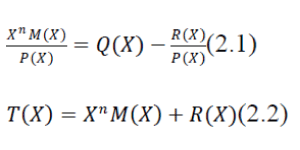 |
||||||||
| An error E(X) will only be undetectable if it is divisible by P(X). It can be shown [PETE611 that all of the following errors are not divisible by a suitably chosen P(X) and, hence, are detectable: | ||||||||
| If G contains two or more terms, all single-bit errors are detected. | ||||||||
| If G is not divisible by x (that is, if the last term is 1), and e is the least positive integer such that G evenly divides xe+ 1then all double errors that are within a frame of e bits are detected. A particularly good polynomial in this respect is x15 + x14 + 1 for which e=32767 | ||||||||
| If x + 1 is a factor of G, all errors consisting of an odd number of bits are detected. | ||||||||
| An r-bit CRC checksum detects all burst errors of length ≤ r (A burst error of length r is a string of r bits in which the first and last are in error, intermediate r - 2 bits may or may not be in error.) | ||||||||
| In addition, it can be shown that if all error patterns are considered equally likely, then for a burst error of length r + 1, the probability that E(X) is divisible by P(X) is 1 2 1 , and for a longer burst, the probability is 1 2 , where r is the length of the FCS[4]. | ||||||||
| Four versions of P(X) shown in Table Iare widely used: | ||||||||
IMPLEMENTATION |
||||||||
| The design is simulated via Proteus ISIS v7.6 sp4 provided by Labcenter Electronics. The design is created using Schematic Capture and same is simulated. | ||||||||
A. Keyboard |
||||||||
| US layout keyboard is used to feed the data into controller onto the user input, The data input from the keyboard is manipulated as per the code and results are transmitted via Serial Communication using SCI protocol. | ||||||||
B. Serial Communication |
||||||||
| Data is transmitted serially i.e. bit by bit using Serial Communication Interface (SCI). The transmission is done by means of UART: 1 start bit, 8 bit data, 1 stop bit; thus forming a frame, which is transmitted at the desired baud rate. The data transmitted is displayed on the Virtual Terminal Screen provided on the simulation platform. Fig. 3.1 shows the Virtual Terminal Screen used in Proteus to display the data being transmitted. | ||||||||
| The baud rate is so adjusted to match with the controller and virtual terminal transceiver. The controller is loaded with the count and thus desired baud rate is obtained. | ||||||||
C. Microcontroller AT89C55 |
||||||||
| The AT89C55WD is a low-power; high-performance CMOS 8-bit microcontroller with 20K bytes of Flash programmable read only memory and 256 bytes of RAM. The device is manufactured using Atmel’s high-density nonvolatile memory technology and is compatible with the industry standard 80C51 and 80C52 instruction set and pinout. The on-chip Flash allows the program memory to be user programmed by a conventional non-volatile memory programmer. By combining a versatile 8-bit CPU with Flash on a monolithic chip, the Atmel AT89C55WD is a powerful microcomputer which provides a highly flexible and cost effective solution to many embedded control applications. | ||||||||
| The microcontroller is programmed with Embedded C language using Keil cross-compiler and Intel-hex file is generated and embed into the controller to simulate the results. Microcontroller is embedded with the generated hex file and design is simulated to get optimum results. | ||||||||
WORKING PRINCIPLE |
||||||||
| In networking systems a significant role of the Data Link layer is to convert the potentially unreliable physical link between two machines into an apparently very reliable link. This is achieved by including redundant information in each transmitted frame. Depending on the nature of the link and the data, one can include just enough redundancy to make it possible to detect errors and then arrange for the retransmission of damaged frames. The cyclic redundancy check or CRC is a widely used parity bit based error detection scheme in serial data transmission applications. This code is based on polynomial arithmetic. | ||||||||
| The bits of data to be transmitted are the coefficients of the polynomial. As an example, the bit stream 1101011011 has 10-bits, representing a 10-term polynomial: | ||||||||
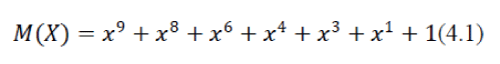 |
||||||||
| To compute the CRC of a message, another polynomial called the generator polynomial G(x) is chosen. G(x) should have a degree greater than zero and less than that of the polynomial M(x). Another requirement for G(x) is a non-zero coefficient in the x0 term. This results in several possible options for the generator polynomial, and hence the need for standardization. CRC-16 is one such standard that uses the generating polynomial: | ||||||||
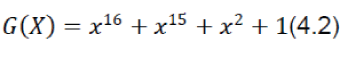 |
||||||||
| CRC-16 detects all single and double errors, all errors with an odd number of bits, all burst errors of length 16 or less, and most errors for longer bursts. CRC-32 uses the generating polynomial: | ||||||||
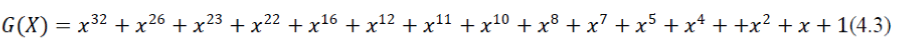 |
||||||||
| In general, an n-bit CRC is calculated by representing the data stream as a polynomial M(x), multiplying M(x) by x^n (where n is the degree of the polynomial G(x)), and dividing the result by a generator polynomial G(x). The resulting remainder is appended to the polynomial M(x) and transmitted. The complete transmitted polynomial is then divided by the same generator polynomial at the receiver end. If the result of this division has no remainder, there are no transmission errors. Mathematically, this can be represented as: | ||||||||
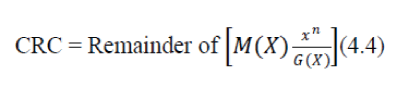 |
||||||||
| CRC computation involves manipulating M(x) and G(x) using modulo 2 arithmetic. Modulo arithmetic yields the same result for addition and subtraction. Therefore it is necessary only to consider three operations involving polynomials namely, addition, multiplication, and division. [6] | ||||||||
ALGORITHM |
||||||||
| Cyclic redundancy check is a way of providing error control coding in order to protect data by introducing some redundancy in the data in a controlled fashion. It is a commonly used and very effective way of detecting transmission errors. | ||||||||
| The CRC encoding procedure is described by equation 5.1 | ||||||||
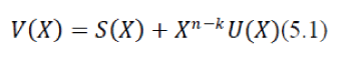 |
||||||||
| Where V(x) is the n bit long data word transmitted and it consists of the original data and U(x) followed by a code word S(x) called the CRC-sum. S(x) represents the extra bits added to a message in order to provide redundancy so that errors during transmission can be detected. The length of S(x) is denoted by the constraint length. S(x) is computed according to equation 5.3. | ||||||||
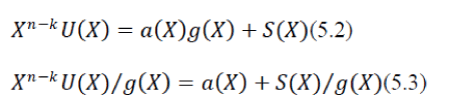 |
||||||||
| S(x) is in other word means the remainder resulting from a division of the data stream and a generator polynomial g(x). Since all code words are divisible by g(x) the remainder of the left hand side of equation has to be zero for a real codeword. The actual coding procedure is the same at both the receiving and transmitting end of the line. | ||||||||
| The CRC encoding/decoding principle is illustrated in Fig. 5.1 and the parallel logic implementation is shown in Fig. 5.2, the receiver performs a CRC-check on the incoming message and if the result (S(x)) is zero, then the transmission is error free. One more practical way of solving this is to compute the CRC only for the first part of the message U(x), and then perform a bitwise 2’s-complement addition with the computed checksum S(x) on the transmission side. If the result is non-zero the receiver will order a retransmission from the sender. [5] | ||||||||
RESULTS |
||||||||
| The proposed design is simulated on the simulation platform. The virtual terminal screen displayed the message bits being transmitted and CRC-generator polynomial used to compute the Source CRC. The data appended with CRC is transmitted over the channel and tested for its veraciousness. Fig. 6.1 shows the Virtual Terminal Screenshot used for computation in CRC. | ||||||||
CONCLUSION |
||||||||
| Cyclic Redundancy Check used to detect errors in the transmission of the data over the channel. The CRC generated by means of the CRC generator suffixed with the message bits is transmitted over the channel. The received code word is again validated by means of the same CRC generator polynomial. If remainder is zero, then its validity is proved else the erroneous frame is retransmitted. | ||||||||
Tables at a glance |
||||||||
|
||||||||
Figures at a glance |
||||||||
|
||||||||
References |
||||||||
|