International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

DECISION TREE LEARNING WITH ERROR CORRECTED INTERVAL VALUES OF NUMERICAL ATTRIBUTES IN TRAINING DATA SETS

C. SUDARSANA REDDY1, S. AQUTER BABU2 and Dr. V. VASU3
  1. Department of Computer Science and Engineering, S.V. University College of Engineering, S.V. University, Tirupati, Andhra Pradesh, India
  2. Assistant Professor of Computer Science, Department of Computer Science, Dravidian University, Kuppam - 517425, Chittoor District, Andhra Pradesh, India
  3. Department of Mathematics, S.V. University, Tirupati, (A.P), India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Classification is the most important technique in data mining. A Decision tree is the most important classification technique in machine learning and data mining. Data measurement errors are common in any data collection process, particularly when the training datasets contain numerical attributes. Values of numerical attributes contain data measurement errors in many training data sets. We extend certain or traditional or classical decision tree building algorithms to handle training data sets with numerical attributes containing measurement errors. We have discovered that the classification accuracy of a certain or classical or traditional decision tree classifier can be much improved if the data measurement errors in the values of numerical (or continuous) attributes in the training data sets are properly controlled (corrected or handled) appropriately. The present study proposes a new algorithm for decision tree classifier construction. This new algorithm is named as Interval Decision Tree (IDT) classifier construction. IDT classifiers are more accurate and efficient than certain or traditional decision tree classifiers. An interval is constructed for each value of each attribute in the training data set and within the interval the best error corrected value is approximated and then entropy is calculated. Extensive experiments have been conducted which show that the resulting IDT classifiers are more accurate than certain or traditional or classical decision tree classifiers.

Keywords
error corrected interval values of the numerical attributes in the training data sets; measurement errors in the values of numerical attributes in the training data sets; training data sets containing numerical attributes; training data sets; decision tree; classification.

INTRODUCTION
Decision tree induction is the learning of decision trees from class labeled training tuples [1]. Two most important features of decision tree are comprehensibility and interpretability [1]. One of the most popular classification models is the decision tree model [3]. When decision trees are used for classification they are called classification trees [2]. Decision trees are popular because they learn and respond quickly and accurate in many domains [2]. In general, training data sets contain both numerical (continuous) and categorical (discrete) attributes. Raw measured data values of numerical attributes normally contain measurement errors. A new decision tree classifier construction method is proposed based on the error correction in the interval and it constructs more accurate decision tree classifiers.
In traditional or classical decision tree classification, decision tree classifiers are constructed directly from the values of the attributes of the training data sets without considering measurement errors in the values of numerical attributes in the training data sets. We call this approach certain decision tree (CDT). Another interval based approach during the decision tree classifier construction is to consider the data measurement errors present in the values of numerical attributes of training data sets. We call this approach Interval Decision Tree (IDT) classifier construction method. The present study has verified experimentally through simulation the performance of both CDT and IDT.
In this paper a new decision tree classifier construction algorithm is proposed. The new decision tree classifier construction algorithm, IDT, takes care of measurement errors present in the values of numerical attributes in the training data sets by constructing an interval around each value of each attribute in the training data set. Interval decision tree (IDT) classifier construction method can build significantly more accurate decision trees than certain decision tree (CDT) classifier construction methods. High classification accuracies can be achieved by using Interval decision trees (IDTs). Interval decision tree (IDT) construction method can potentially build more accurate decision trees because it takes measurement error information into account by constructing an interval for each value of attribute.
We cannot always assume that the training data sets are error free [3]. It is likely that some sort of measurement errors are incurred in the data collection process of these training data sets [3]. The errors may occur in random fashion. Sometimes the errors in the values of the numerical attributes in the training data sets can be modeled using statistical distributions such as Gaussian and Uniform distributions. In the case of random noise better to use Gaussian distribution to model errors present in the values of the numerical attributes in the training data sets. Many data sets with numerical attributes have been collected via repeated measurements and the process of repeated measurements is the common potential source of getting measurement errors in the values of numerical attributes in the training data sets. Sometimes values of numerical attributes in the training data sets are collected over an unspecified number of repeated measurements [3].
Data obtained from measurements by physical devices are often inaccurate due to measurement errors [3]. Another source of error is quantization errors introduced by the digitization process [3]. Such errors can be properly handled by assuming an appropriate error correcting model such as Gaussian error distribution for random noise or a uniform error distribution for quantization errors [3].
Errors play an important role in every scientific and medical experiment. There exists many data errors, and random errors are the most important data errors to be considered in scientific and medical experiments. This paper mainly concentrates to find and correct random errors present in the values of numerical attributes in the training data sets by systematically adjusting various random data error values in the constructed interval of each value of each numerical attribute of the training dada sets. Decision trees have been well recognized as a very powerful and attractive classification tool [4]. Errors in scientific experiments are extremely well approximated by a normal distribution [5]. Normal distribution equation is also derived from a study of errors in repeated measurements of the same quantity [5]. The term continuous is used in the literature to indicate both real and integer valued attributes [8].

PROBLEM DEFINITION
In many real life applications training data sets are not error free due to measurement errors in data collection process. In general, values of numerical attributes in training data sets are always inherently associated with errors. Different types of errors present in the training data sets are not considered during decision tree construction of existing decision tree classifiers. Hence, classification results of existing decision tree classifiers are less accurate or inaccurate in many cases because of different types of data errors present in the training data sets. Hence previous data mining methods must be reconsidered.
As data errors are associated with almost all training data sets containing numerical attributes, it is important to develop more accurate and more efficient data mining techniques by taking error corrected data values of numerical attributes of the training data sets. Sometimes, for preserving data privacy training dada sets are modified explicitly by incorporating certain data error values into the values of numerical attributes in training data sets. In such cases training dada sets contain errors with modified attribute values. Such modified data sets must be reconstructed by eliminating explicitly injected data errors into the training data sets.

EXISTING ALGORITHM

A. Certain Decision Tree (CDT) Algorithm Description
The certain decision tree (CDT) algorithm constructs a decision tree classifier by splitting each node into left and right nodes. Initially, the root node contains all the training tuples. The process of partitioning the training data tuples in a node into two subsets based on the best split point value zT of best split attribute???? ?? and storing the resulting tuples in its left and right nodes is referred to as splitting. Whenever further split of a node is not required then it becomes a leaf node referred to as an external node. All other nodes except root node are referred as internal nodes. The splitting process at each internal node is carried out recursively until no further split is required. Continuous valued attributes must be discretized prior to attribute selection [6]. Further splitting of an internal node is stopped if one of the stopping criteria given hereunder is met.
1.All the tuples in an internal node have the same class label. 2. Splitting does not result nonempty left and right nodes.
In the first case, the probability for that class label is set to 1 whereas in the second case, the internal node becomes external node. The empirical probabilities are computed for all the class labels of that node. The best split pair comprising an attribute and its value is that associated with minimum entropy.
Entropy is a metric or function that is used to find the degree of dispersion of training data tuples in a node. In decision tree construction the goodness of a split is quantified by an impurity measure [2]. One possible function to measure impurity is entropy [2]. Entropy is an information based measure and it is based only on the proportions of tuples of each class in the training data set. Entropy is used for finding how much information content is there in a given data [1].
Entropy is taken as dispersion measure because it is predominantly used for constructing decision trees. In most of the cases, entropy finds the best split and balanced node sizes after split in such a way that both left and right nodes are as much pure as possible. Accuracy and execution time of CDT algorithm for 9 data sets are shown in Table 5.2 .
Entropy is calculated using the formula
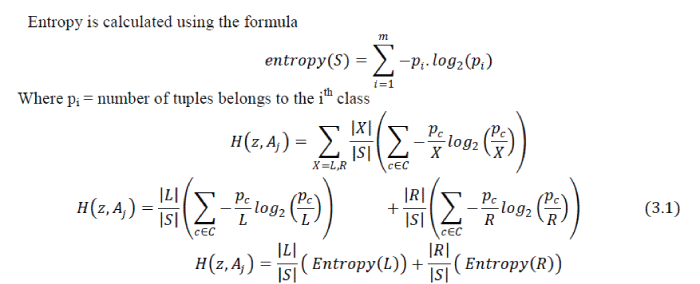equation
Where
• Aj is the splitting attribute.
• L is the total number of tuples to the left side of the split point z.
• R is the total number of tuples to the right side of the split point z.
• pc/L is the number of tuples belongs to the class label c to the left side of the split point z.
• pc/R is the number of tuples belongs to the class label c to the right side of the split point z.
• S is the total number of tuples in the node.

B. Pseudo code for Certain Decision Tree (CDT) Algorithm CERTAIN_DECISION_TREE (T)
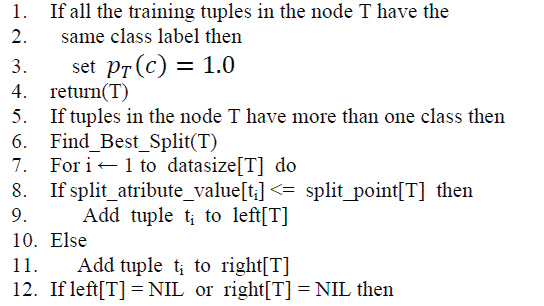equation
13. Create empirical probability distribution of the node T
14. return(T)
15. If left[T] != NIL and right[T] != NIL then
16. CERTAIN _DECISION_TREE(left[T])
17. CERTAIN _DECISION_TREE(right[T])
18. return(T)

PROPOSED ALGORITHM

A. Proposed Interval Decision Tree (IDT) Algorithm Description
The procedure for creating Interval Decision Tree (IDT) classifier is same as that of Certain Decision Tree (CDT) classifier construction except that IDT calculates entropy values for error corrected data values in the numerical attributes of the training data sets by constructing intervals. Errors in the values of numerical attributes in the training datasets are calculated based on the assumption that training data sets contain measurement errors particularly when the training data sets contain numerical attributes.
For each value of each numerical attribute an interval is constructed and within the interval entropies are computed for error corrected values and the point with minimum entropy is selected. Based on the assumption that measurement errors are inevitable in the values of numerical attributes in the training dada sets, errors are corrected in the values of numerical attributes by assuming 1% or 0.1% or 0.01% errors in the values of attributes and then entropy is calculated for each value of each numerical attribute in the training data set.
For example, an interval is constructed for each value in the training data set and then within each interval, measurement errors are corrected by gradually decreasing or increasing assumed measurement error values at „n? points and then entropy is calculated for all those error corrected „n? points and then finally one best optimal point which gives minimum entropy is selected within the interval.
For example, if the value of a numerical attribute is 7 then an interval [7 – 7*0.1,7 + 7*0.1] or [7–7*0.01, 7+ 7*0.01] or [7 – 7*0.001, 7 + 7*0.001] is constructed and within the interval errors are corrected and entropy is calculated at „n? points and then one optimal point is selected in the interval. Computational complexity of IDT is more than CDT.
To reduce the computational complexity of IDT we have proposed a pruning technique so that entropy is calculated only at one best point for each interval. Hence, the new approach, IDT, for decision tree classifier construction is more accurate with approximately same computational complexity as that of CDT.
Extensive experiments have been conducted which show that the resulting experiments are more accurate than those of certain decision trees (CDT). IDT can build not only more accurate decision tree classifier but also it is more efficient than CDT and Execution times of both the algorithms are approximately same. The present study has verified experimentally through simulation the performance of two algorithms.
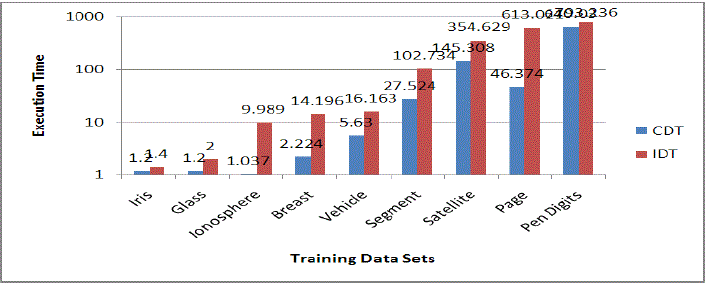
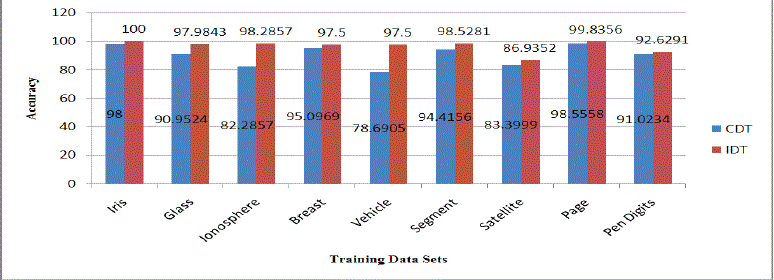
Accuracy and execution time of ADT algorithm for 9 data sets are shown in Table 5.3 and comparison of execution time and accuracy for CDT and ADT algorithms for 9 data sets are shown in Table 5.4 and charted in Figure 5.1 and Figure 5.2 respectively.

B. Pseudo code for Interval Decision Tree (IDT) Algorithm

INTERVAL_DECISION_TREE (T)
1. If all the training tuples in the node T have the
2. same class label then
3. set pT(c) = 1.0
4. return(T)
5. If tuples in the node T have more than one class then
6. For each value of each numerical attribute construct an interval and then find entropy at ‘n’ error corrected values in the interval gradually by decreasing or increasing error levels from first point to last point in the interval and then select one optimal point, point with the minimum entropy, in the interval.
7. Find_Best_Split(T)
8. For i ← 1 to datasize[T] do
9. If split_atribute_value[ti] <= split_point[T] then
10. Add tuple ti to left[T]
11. Else
12. Add tuple ti to right[T]
13. If left[T] = NIL or right[T] = NIL then
14. Create empirical probability distribution of the node T
15. return(T)
16. If left[T] != NIL and right[T] != NIL then
17. INTERVAL _DECISION_TREE(left[T])
18. INTERVAL _DECISION_TREE(right[T])
19. return(T)

EXPERIMENTAL RESULTS
A simulation model is developed for evaluating the performance of two algorithms: Certain Decision Tree (CDT) and Interval Decision Tree (IDT) experimentally. The data sets shown in Table 5.1 from University of California (UCI) Machine Learning Repository are employed for evaluating the performance of the above said algorithms.
In all our experiments we have used data sets from the UCI Machine Learning Repository [6]. 10-fold crossvalidation technique is used for test tuples for all training data sets with numerical attributes except Satellite and PenDigits training data sets [6]. For Satellite and PenDigits training data sets with numerical attributes a separate test data set is used for testing.
The simulation model is implemented in Java 1.7 on a Personal Computer with 3.22 GHz Pentium Dual Core processor (CPU), and 2 GB of main memory (RAM). The performance measures, accuracy and execution time (in seconds), for the above said algorithms are presented in Table 5.2 to Table 5.4 and Figure 5.1 to Figure 5.2.

CONCLUSIONS

A. Contributions
The performance of existing traditional or classical or certain decision tree (CDT) is verified experimentally through simulation. A new decision tree classifier construction algorithm called Interval Decision Tree (IDT) is proposed and compared with the existing Certain Decision Tree classifier (CDT). It is found that the classification accuracy of proposed algorithm (IDT) is much better than CDT algorithm.

B. Limitations
Proposed algorithm, Interval Decision Tree (IDT) classifier construction, handles only measurement errors present in the values of numerical attributes of the training data sets. Also execution time of IDT is more for many of the training data sets.

C. Suggestions for future work
Special techniques or ideas or plans are needed to find and correct data errors other than measurement errors that are present in the values of numerical attributes of the training data sets. Special pruning techniques are needed to reduce execution time of IDT. Also special techniques are needed to find and correct errors in the categorical attributes.

Tables at a glance
Table icon Table icon Table icon Table icon
Table 5.1 Table 5.2 Table 5.3 Table 5.4
 

Figures at a glance
Figure Figure
Figure 5.1 Figure 5.2
 

References