Design a Transmission Policies for Decode
and Forward Relaying in a OFDM System

R.Krishnamoorthy; N.S. Pradeep; D.Kalaiselvan

Design a Transmission Policies for Decode and Forward Relaying in a OFDM System

R.Krishnamoorthy¹, N.S. Pradeep² , D.Kalaiselvan³

Professor, Department of CSE, University College of Engineering, Tiruchirapalli, India.
Assistant Professor, Department of ECE, University College of Engineering, Tiruchirapalli, India.
ME (Communication Systems), Student, University College of Engineering, Tiruchirapalli, India.

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Orthogonal Frequency Division Multiplexing (OFDM) is a leading physical layer transmission technique for high spectral efficiency and date rate in broadband wireless communication systems. Combining relaying architecture with OFDM transmission is a powerful technique for broadband wireless communication, and thus adopted in many current and next generation standards. Design of new transmission policies to improve Quality of Service (QoS) of OFDM bidirectional Decode and forward relaying has been proposed in this work. Where a pair of user exchange the information via assistance of Decode and Forward(DF) relay. Each user can communicate with other via three transmission mode: Direct transmission, one way relaying and two way relaying. We jointly optimize the transmission policies, including power allocation, transmission mode selection and sub carrier allocation has been considered. This is formulated mixed integer problem. Solve the problem in an asymptotically optimal manner by using dual method. The simulation result show that the proposed scheme can substantially improve system performance.

Keywords

Two-way relaying, Decode-and-Forward (DCF), resource allocation, Orthogonal Frequency Division Multiplexing (OFDM), Multiple Input and Multiple Output (MIMO).

INTRODUCTION

Orthogonal Frequency Division Multiplexing (OFDM) provides a multiple-access method, as known as OFDMA by allocating different subcarriers to different users in multiuser environments On the other hand, cooperative relay has received much interests due to its capabilities of improving system performance, such as throughput enhancement, power saving, and coverage extension Combining relaying architecture with OFDM transmission is a powerful technique for broadband wireless communication, and thus adopted in many current and next generation standards However, the traditional one-way relaying is less spectrally efficient due to the practical half-duplex constraint. To overcome this problem, two-way relaying has been proposed to before several years it is promising and attractive to exploit network coding gain by dynamic resource allocations for improving spectral efficiency in OFDM bidirectional relay systems. There are several works on resource allocation in OFDM bidirectional relay systems.

These works can be divided into two categories are per-subcarrier basis and subcarrier pairing basis. The first category assumes that the two-hop cooperative transmission, source-to-relay link and relay-to-destination link use the same subcarrier. Such per-subcarrier basis significantly simplifies the optimization problems but does not fully utilize the channel dynamics. For instance, the power and subcarrier allocation for OFDM two-way relaying with both amplify-and-forward (AaF) and decode-and-forward (DaF) strategies. By using dual decomposition method, the problem was decomposed into per-subcarrier sub problems that can be solved independently. A two-step suboptimal method for power allocation for OFDM two-way AF relaying was used, where power is first allocated in each subcarrier for a given per-subcarrier power constraint, then the per-subcarrier power constraints are coordinated to satisfy a total peak power constraint of the system. The optimal power allocation for OFDM two-way AF relaying with a total peak power constraint turns out to be two-step approaches. Different from the per-subcarrier basis, the subcarrier pairing basis allows the subcarriers in the first and second hops to be paired and then a better performance can be provided. In power was first allocated by water-filling and then subcarriers were paired by a greedy heuristic method for OFDM two-way AF relaying. The subcarrier pairing based joint optimization problem of transmission mode selection, subcarrier assignment, and relay selection for OFDMA bidirectional relay cellular networks by an ant colony optimization method from a graph theoretical perspective. The optimal subcarrier and relay assignment for OFDM twoway relay system are used for bipartite graph matching algorithm.

PROPOSED METHOD

In this paper as proposes in future application in Real time to the concept of neither per-subcarrier basis nor subcarrier pairing basis is optimal for two-way DaF relaying, the parallel OFDM relaying architecture, the bidirectional communication can be completed by three transmission modes and one challenging issue to be addressed for future developments of wireless networks is how to meet user’s diverse quality-of-service (QoS) requirements. Those thinks are either match or not in future technologies and Real time Applications.

The joint optimization problem of power allocation, subcarrier assignment, and transmission mode selection with QoS guarantees in OFDM-based bidirectional transmission systems. By using the dual method, we efficiently solved the mixed integer programming problem in an asymptotically optimal manner

A few interesting conclusions have been obtained through simulations. First, the significance of one-way relaying is decreasing with SNR. Second, the throughput percentages of direct transmission and two-way relaying are increasing with SNR, and two-way relaying dominates the system performance. Third, for a given user, one-way relaying contributes more throughputs with the increasing rate requirements, and direct transmission performs oppositely. Finally, direct transmission dominates the system performance when the relay is closer to either of the two users, and one- and two-way relay work well when the relay locates at the midpoint of the two users.

The joint optimization problem of power allocation, subcarrier assignment, and transmission mode selection for OFDM bidirectional DF relaying does not match for existing paper, to save the power in allocation of nodes, many other blocks in proposed flow diagram as shown in following topics, then the

In receiver diversity of MRC techniques are realized practical receiver model for decode-and-forward Cooperative multiple-access transmission was proposed. The model adopted a dynamic-blind calculation of the combiner's weighting factor ¸ that was presented and its approximate expression was provided. Using the suboptimum receiver, the analytical closed-form performance under several channel conditions was used as a reference level and compared to the performance using the proposed estimation. It provided an performance and illustrated remarkable accuracy as the value of approaches Moreover, it was simple, adaptive, and completely blind as it does not required any prior knowledge of the transmission conditions. Then, the proposed channel blind receiver was evaluated as a substitute to the sub-optimum receiver model using the closed-form performance, and it showed a reliable performance as well as simplicity.

One of the key expectations for the 4th Generation (4G) wireless system is to provide ubiquitous high data rate coverage. During these recent years, a large part of the research has focused on MIMO-OFDMA transmission technology. MULTIPLE-input multiple-output (MIMO) and orthogonal frequency division multiple access (OFDMA) are important techniques for high data rate wireless multiuser communication systems, such as 3GPP Long Term Evolution(LTE) and IEEE 802.16 Worldwide Interoperability for Microwave Access (WiMAX), not only because of its flexibility in resource allocation, but also because of its ability to exploit multiuser diversity.

On the other hand, cooperative relaying for wireless networks has received considerable interest, as it provides coverage extension and reduced power consumption without incurring the high costs of additional base station (BS) deployment. There are two main types of relaying schemes, namely half-duplex (HD) relaying and full duplex (FD) relaying. A large amount of work has been devoted to HD relaying as it enables a low-complexity relay design. Nevertheless, HD relaying systems require additional resources to transmit data in a multi-hop manner which results in a loss of spectral efficiency. Even though there several approaches for minimizing recovering the spectral efficiency loss associated with HD relaying, such as non-orthogonal relaying and two-way relaying.

In these schemes do not solve the problem fundamentally since the associated protocols are still using HD relaying. On the contrary FD relaying suffers from inherent loop interference which was considered impractical in the past.

Recent research shows that FD relaying is feasible by using interference cancellation techniques and transmit receive antenna isolation. Several prototypes of FD transceivers using different self-interference cancellation techniques have been built to demonstrate the feasibility of FD relaying and the expected performance gains compared to HD relays. However, efficient resource allocation and scheduling algorithms for MIMO-OFDMA FD relaying systems with interference cancellation error have not been studied, yet. A lot of work has been done on Amplify-and- Forward relaying in this paper we evaluate the performance of the Decode-and-Forward relaying protocol. It is based on current and future generation oriented.

OPTIMIZATION FRAMEWORK

a. System Model

We consider the relay-assisted bidirectional communication as shown in Fig. 1, which consists of a pair of users A and B, and a single relay R. Each user can communicate with the other directly or through the relay. Thus, each user can communicate with the other via three transmission modes, namely, direct transmission, one- and twoway relaying. In this paper, the two-phase two-way relaying protocol is applied, second phase is the broadcast (BC) phase [1]–[3]. Each node can transmit and receive at the same time but on different frequencies. For both one-way relaying and two-way relaying, the relay adopts DF strategy and the delay between the first and second hops can be negligible compared with the duration of a transmission frame. For example, Fig. 1 shows that A and B can use subcarrier {9} for the MAC phase but the relay can use subcarriers {7, 8} in the BC phase. Notice that such subcarrier set basis relaying is also applicable for one-way relaying.

b. Channel Model

The wireless channels are modeled by large-scale path loss, shadowing, and small-scale frequency-selective Rayleigh fading. It is assumed that the transmission to both users is divided into consecutive frames, and the fading remains unchanged within each transmission frame but varies from one frame to another. We also assume that channel estimation is perfectly known at all nodes. Note that in relay-assisted systems such as IEEE 802.16m, relay nodes are usually fixed. Such that the task of centralized resource allocation can be embedded at the relay. Without loss of generality, the additive white noises at all nodes are assumed to be independent circular symmetric complex Gaussian random variables, each having zero mean and unit variance. The channel coefficients from node j to node j_ on subcarrier n are denoted as hi,j, n, where j, j_ ∈ {A,B,R},

c. Problem Formulation

We use superscripts a,b,and c to denote direct transmission, one-way relaying, and two-way relaying, respectively. We first introduce the following three sets of binary assignment variables with respect to the three transmission modes:

- ρa k,n indicates whether subcarrier n is assigned to user k for direct transmission, k ∈ {A,B}.

- ρb k,n indicates whether subcarrier n is assigned to user k at the i-th hop of one-way relaying, k ∈ {A,B}, i = 1,

- ρc k,n indicates whether subcarrier n is assigned to the user pair at the i-th hop of two-way relaying, i = 1, 2.

As mentioned in previous works [8], [9], [10], the bidirectional links must occur in pair for two-way relaying. Therefore, in our case, the user index k is not involved in ρc n,i .In order to avoid interference, these binary variables must satisfy the following constraint:

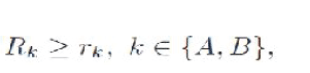where rk is the minimum rate requirements of user k. Our objective is not only to optimally assign subcarriers and transmission modes but also to allocate power and rate for each user so as to maximize the weighted sum rates while maintaining the individual rate requirements of each user. Mathematically, the joint optimization problem can be formulated as (P1)

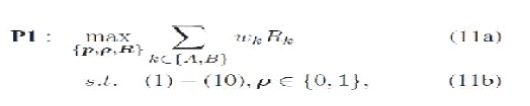Comparing with the related works [4]–[9], there are several unique features about our problem formulation P1. First, we jointly optimize subcarrier assignment, transmission mode selection, and power allocation. The previous works only consider partial resources of P1. Second, P1 represents the first attempt that optimizes OFDM two-way DF relaying based on subcarrier set basis, according to the derived capacity region in (8). Third, P1 considers individual rate-QoS for each user, and we impose three transmission modes simultaneously to support the individual QoS but over different sets of subcarriers, thanks to the parallel structure of OFDM relaying.

OPTIMAL TRANSMISSION POLICY

The problem in P1 is a mixed integer optimization problem. Finding the optimal solution needs exhaustive search with exponential complexity, where each subcarrier has eight possibilities of assignments over different users, different transmission modes, along with different hops. Total N subcarriers are used and therefore total 8N possibilities of assignments are needed. Then, power allocation is performed for each assignment (the pure power allocation problem is convex if the assignment is fixed), and the optimal solution follows the assignment that results in maximum throughput. In this section, we present an efficient method to find the asymptotically optimal solution of P1 with linear complexity in the number of subcarriers.

It is easy to find that each element of R has the form of ρ log2(1 + s/ρ) that is jointly concave in (ρ, s), where ρ and s represent the general expressions of the elements in ρ and s, respectively. Thus, the objective function of P2 is concave since any positive linear combination of concave functions is concave. Moreover, the constraints (12b), (12c) and (1) are affine, and the other constraints are convex. Therefore, P2 is a convex optimization problem.

We first introduce non-negative Lagrangian multipliers λb1 k and λb2 k related with the rates of the first and second hop for one-way relaying in (7), respectively, and λc1 k, λc2 k, and λc AB associated with the three rate constraints for two-way relaying in (8), respectively. All of them are denoted as λ _ 0. In addition, non-negative Lagrangian multipliers α = {αA, αB, αR} _ 0 are introduced to associate with the power constraints of the three nodes, μ = {μA, μB} _ 0 are associated the two users’ QoS requirements in (10). Then the dual function of P2 can be defined as

By substituting these results above into (14), the Lagrangian can be rewritten as:

(30) and (31) show that the optimal power allocations for DF one-way relaying are also achieved by multi-level waterfilling.

3) Maximizing Lagrangian over ρ: Substituting the optimal power allocations s(λ,α,μ) into (13) to eliminate the power variables, the profits (21)-(25) in the sub-Lagrangian (28) can be rewritten as respectively

Algorithm 1 Proposed dual-based method for P1

1: initialize {λ,α,μ}.

2: repeat

3:Compute the profits

Using the optimal power allocations s*(λ,α,μ) for all k and n.

4: Compare the profits for each subcarrier n, and let the maximum profit be active and others inactive. Then the optimal ρ*(λ,α,μ) can be obtained.

5: Update {λ,α,μ} using the ellipsoid method as the

following steps 6-10:

6: if the constraints (39)-(41) are all satisfied then

7: Update ellipsoid with Δ defined in Proposition 3.

8: else

9: Update the ellipsoid with the gradient of the constraints(39)-(41).

10: end if

11: until {λ,α,μ} converge.

12: if RA ≥ rA and RB ≥ rB then

13: QoS requirements are satisfied and output RA and RB.

14: else

15: Declare an outage and output RA = RB = 0.

16: end if

The detailed update rule can be found in [27]. In Algorithm 1, for given transmit powers, the system is said to be in an outage if any QoS rate requirement can not be satisfied. In this case, we set the rates as zero. The computational complexity of the ellipsoid method is O(q2), where q is the number of the dual variables and q = 10 in our case. Combining the complexity of decomposition in (26), the total complexity of the proposed algorithm is O(q2N), which is linear in the number of subcarriers.

SIMULATION RESULT

The below graph is shows in three different output signals. In Detect and Forward signals, SNR will be increases the BER is decreases. It plots the above graph as shows. The incoming signals are only to detect then the signals are forwarding. The received signal is weak signals that the signals detect and forward means, the output signals is very low at same time the efficiency is very low.

In Amplifying and Forwarding signals, SNR will be increases the BER is decreases. It plots the above graph as shows. The receiving signals are weak and strength both signals are commonly amplified, then the signals are forwarding. The receiving signals are includes interference, noise, distraction, weak and strength signals. In this block total signals are amplified so, the above parameters are amplified. The interference, noise, distraction parameters strengths are improving the spectral efficiency is reduced. So, this method is not suitable for more communication purposes.

In Decode and Forwarding signals, SNR will be increases the BER is decreases. It plots the above graph as shows. It overcomes to the drawback of detect and forwarding and amplifying and forwarding functions. The relay node is decodes form encodes channel. Then, it moves to amplifying and forwarding block. That blocks to amplify after to forwarding next stage.

The compare three signals, the decode and forwarding signals is improving BER in bps and reduce SNR in db level, so it is very good perform compare other two signals.

The policies behind the bidirectional relaying is analyzed and plotted. We are modify the transmission policies to overcome the higher BER problems in lower SNR. The proposed algorithm uses the error free DF and AF concept for the OFDM bidirectional relaying.

CONCLUSION

In this paper, we studied the joint optimization problem of power allocation, subcarrier assignment, and transmission mode selection with QoS guarantees in OFDM-based bidirectional transmission systems. By using the dual method, we efficiently solved the mixed integer programming problem in an asymptotically optimal manner. Simulation results showed that our proposed scheme can outperform the traditional schemes by a significant margin.

A few interesting conclusions have been obtained through simulations. First, The compare three signals, the decode and forwarding signals is improving BER in bps and reduce SNR in db level, so it is very good perform compare other two signals. Second,

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4

References

B. Rankov and A. Wittneben, “Spectral efficient protocols for half duplex fading relay channels,” IEEE J. Sel. Areas Commun., vol. 25, no. 2, pp. 379–389, Feb. 2007.
P. Popovski and H. Yomo, “Physical network coding in two-way wireless relay channels,” in Proc. 2007 IEEE ICC, pp. 707–712.
S. J. Kim, P. Mitran, and V. Tarokh, “Performance bounds for bidirectional coded cooperation protocols,” IEEE Trans. Inf. Theory, vol. 54, no. 11, pp. 5253–5241, Aug. 2008.
K. Jitvanichphaibool, R. Zhang, and Y. C. Liang, “Optimal resource allocation for two-way relay-assisted OFDMA,” IEEE Trans. Veh. Technol., vol. 58, no. 7, pp. 3311–3321, Sep. 2009.
Y.-U. Jang, E.-R. Jeong, and Y. H. Lee, “A two-step approach to power allocation for OFDM signals over two-way amplify-and-forward relay,”IEEE Trans. Signal Process., vol. 58, no. 4, pp. 2426–2430, Apr. 2010.
M. Dong and S. Shahbazpanahi, “Optimal spectrum sharing and power allocation for OFDM-based two-way relaying,” in Proc. 2010 IEEE ICCASP.
C. K. Ho, R. Zhang, and Y. C. Liang, “Two-way relaying over OFDM: optimized tone permutation and power allocation,” in Proc. 2008 IEEE ICC, pp. 3908–3912.
Y. Liu, M. Tao, B. Li, and H. Shen, “Optimization framework and graph-based approach for relay-assisted bidirectional OFDMA cellular networks,” IEEE Trans. Wireless Commun., vol. 9, no. 11, pp. 3490–3500, Nov. 2010.
Y. Liu and M. Tao, “Optimal channel and relay assignment in OFDM based multi-relay multi-pair two-way communication networks,” IEEE Trans. Commun., vol. 60, no. 2, pp. 317–321, Feb. 2012.