ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| S Venkateswara Reddy PG Student (ES&VLSI), Mallineni Lakshmaiah Engineering College, Kanumalla, Andhra Pradesh, India. |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In this paper, a novel multiplier architecture based on ROM approach using Vedic Mathematics is proposed. This multiplier's architecture is similar to that of a Constant Coefficient Multiplier (KCM). However, for KCM one input is to be fixed, while the proposed multiplier can multiply two variables, three variables and so on. The proposed multiplier of 32-bit is implemented on a Spartan xc5s500e III FPGA, it is fast ,less power consumption as compared with Array Multiplier and Urdhava Multiplier for 32-bit cases.
Keywords |
| Vedic Mathematics, Array multiplier, Urdhava Multiplier, Constant Coefficient Multiplier, Ekadikena Purvena. |
INTRODUCTION |
A. WHAT IS THE NEED OF A MULTIPLIER? |
| Multiplication is one of the more silicon-intensive functions, especially when implemented in Programmable Logic. Multipliers are key components of many high performance systems such as FIR filters, Microprocessors, Digital Signal Processors, etc. A system's performance is generally determined by the performance of the multiplier, because the multiplier is generally the slowest element in the system. Furthermore, it is generally the most area consuming. Hence, optimizing the speed and area of the multiplier is a major design issue. |
B. WHERE A MULTIPLIER IS USED? |
| A Multiplier is used in various platforms for various applications. Multipliers used in Mathematics platform are Coefficient Multiplier, Fourier Multiplier, Algebra Multiplier, Lagrange Multiplier, and Characteristic Multiplier. In Electrical Engineering platform Binary multiplier, Array Multiplier, Frequency Multiplier. In Macro Economics Money Multiplier, Fiscal Multiplier, Economics Multiplier. In Warfare as Force Multiplier. In Clock Signal as CPU Multiplier and in Lottery games also multiplier is used. So we came to know that multipliers are used in our daily life for various applications. So to make the multiplier faster, power efficient and to fit in lesser area we are going to use an oldest technique known as Vedic mathematics. |
VEDIC MATHAMATICS |
| Vedic Mathematics hails from the ancient Indian scriptures called “Vedas” or the source of knowledge. This system of computation covers all forms of mathematics, be it geometry, trigonometry or algebra. The striking feature of Vedic Mathematics is the coherence in its algorithms which are designed the way our mind naturally works. This makes it the easiest and fastest way to perform any mathematical calculation mentally. Vedic Mathematics is believed to be created around 1500 BC and was rediscovered between 1911 to 1918 by Sri Bharti Krishna Tirthaji (1884-1960) who was a Sanskrit scholar, mathematician and a philosopher. He organized and classified the whole of Vedic Mathematics into 16 formulae or also called as sutras. |
| These formulae form the backbone of Vedic mathematics. Great amount of research has been done all these years to implement algorithms of Vedic mathematics on digital processors. It has been observed that due to coherence and symmetry in these algorithms it can have a regular silicon layout and consume less area along with lower power consumption. |
ARRAY MULTIPLIER |
| In Array multiplier AND gates are used for generation of the bit-products and adders for accumulation of generated bit products. All bit-products are generated in parallel and collected through an array of full adders or any other type of adders. Since the array multiplier is having a regular structure, wiring and the layout are done in a much simplified manner. Therefore, among other multiplier structures, array multiplier takes up the least amount of area. But it is also the slowest with the latency proportional to O(Wd), where Wd is the word length of the operand. Example I describes the multiplication process using array multiplier and Fig.1 depicts the structure of the same. Instead of Ripple Carry Adder (RCA), here Carry Save Adder (CSA) is used for adding each group of partial product terms, because RCA is the slowest adder among all other types of adders available. In case of multiplier with CSA , partial product addition is carried out in Carry save form and RCA is used only in final addition. |
 |
| Here from the above example it is inferred that partial products are generated sequentially, which reduces the speed of the multiplier. However the structure of the multiplier is regular. |
 |
| Fig 1: Array multiplier using CSA hardware Architecture |
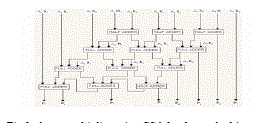
UURDHAVA TIRYAKBHYAM METHOD |
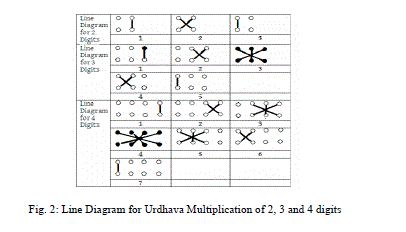
| Urdhava Tiryakbhyam (Vertically and Crosswise), is one of Sixteen Vedic Sutras and deals with the multiplication of numbers. The sutra is illustrated in Example 2 and the hardware architecture is depicted in Fig.2. In this example two decimal numbers (31 x 35) are multiplied. Line diagram for the multiplication of two, three and four digit numbers is shown in Fig. 2 using Urdhava Method. The digits on the two ends of the line are multiplied and the result is added with the previous carry. When three or more lines are present, all the results are added to the previous carry. The least significant digit of the number thus obtained acts as one of the result digit and the rest act as the carry for the next step. Initially the carry is taken to be zero. |
| EXAMPLE 2: 31 x 35 = 1085 |
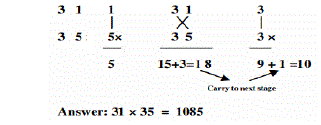 |
 |
PROPSED METHOD |
| The proposed method is based on ROM approach however both the inputs for the multiplier can be variables. In this proposed method a ROM is used for storing the squares of numbers as compared to KCM where the multiples are stored. |
A. OPERATION |
| To find (a x b), first we have to find whether the difference between 'a' and 'b' is odd or even. Based on the difference, the product is calculated. |
B. IN CASE OF EVEN DIFFERENCE |
| Result of Multiplication= [Average] 2- [Deviation] 2 |
C. IN CASE OF ODD DIFFERENCE |
| Result of Multiplication = [Average x (Average + 1)] -[Deviation x (Deviation+ I)] |
| Where |
| Average = [(a+b)/2] |
| Deviation = [Average -smallest (a, b)] |
| Thus the two variable multiplications are performed by averaging, squaring and subtraction. To find the average[(a+b )/2], which involves division by 2 is performed by right shifting the sum by one bit. If the squares of the numbers are stored in a ROM, the result can be instantaneously calculated. However, in case of Odd difference, the process is different as the average is a floating point number. In order to handle floating point arithmetic, Ekadikena Purvena - the Vedic Sutra which is used to find the square of numbers end with 5 is applied. Example 5 illustrates this. In this case, instead of squaring the average and deviation, [Average x (Average + 1)] - [Deviation x (Deviation+ I)] is used. However, instead of performing the multiplications, the same ROM is used and using equation (10) the result of multiplication is obtained. |
| n (n+l) = (n2+n) ... (10) |
| Here n2 is obtained from the ROM and is added with the address which is equal to n(n+l). The sample ROM contents are given in Table 1. |
 |
| TABLE 1 |
| Thus, division and multiplication operations are effectively converted to subtraction and addition operations using Vedic Math’s. Square of both Average and Deviation is read out simultaneously by using a two port memory to reduce memory access time. |
| EXAMPLE 3 |
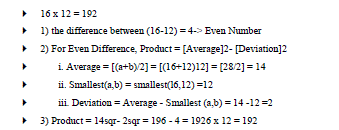 |
| EXAMPLE 4: |
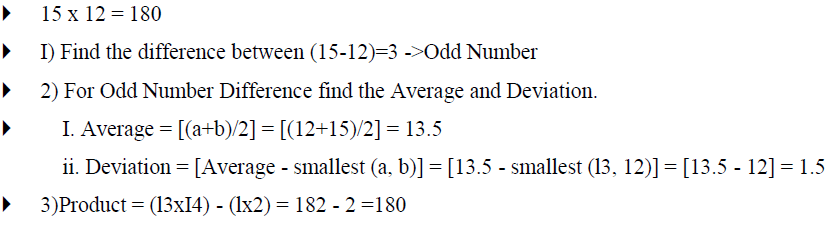 |
EXPERMIMENTAL RESULT |
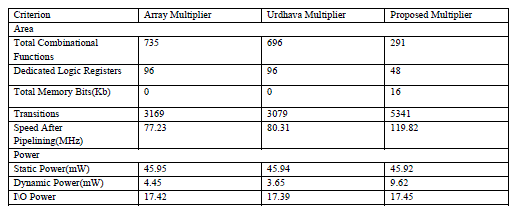
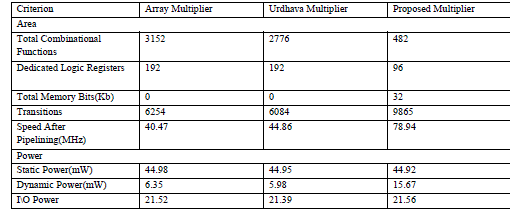
| Table 2 and Table 3, it is inferred that the proposed multiplier is best suited for higher order bit multiplication (i.e., more than SxS). Since in FPGA there is sufficient amount of on chip memory, which can be used to store the squares of the numbers, the proposed multiplier will consume only fewer logic elements for its implementation. |
| TABLE II: Result for 16*16 Multiplier |
 |
| TABLE III: Result for 32*32 Multiplier |
 |
CONCLUSION |
| Thus the proposed multiplier provides higher performance for higher order bit multiplication. In the proposed multiplier for higher order bit multiplication i.e. for 32x32 and more, the multiplier is realized by instantiating the lower order bit multipliers like 16x16. This is mainly due to memory constraints. Effective memory implementation and deployment of memory compression algorithms can yield even better results. |
References |
|