Design and Implementation of Bi-Rotational
CORDIC Algorithm

K.Surya Kumari; S.Jahnavi

Design and Implementation of Bi-Rotational CORDIC Algorithm

K.Surya Kumari ¹, S.Jahnavi²

M.Tech, Asso. Professor, Dept of Electronics & Communication Engineering, Pragati Engineering College, Surampalem, AP, India
M.Tech Student, Dept of Electronics & Communication Engineering, Pragati Engineering College, Surampalem, AP, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The CORDIC algorithm is a repetitive calculation approach ability of emerging different basic functions with a proper shift-and-add method Used to evaluate a large amount of functions. It contains no. of addersub tractors, shift registers with respect to complexity of operation. In this paper we present improved method of shifting by using an alternate scheme by increasing the no. of barrel shifters with increasing pre shifting method and Fault Tolerance in Bi Rotational CORDIC circuits Higher rate of accuracy in fixed and known rotations. The improvement in the fixed angle Rotation reducing the area- and Complexity in the application. From the basic architecture of cordic an Fixed angle rotation is implemented by vector rotation. the rotation of vectors uncontrolled by the circuit till all rotations are completed it will results large system gain and unpredictable angles for effective operation of known angles in this paper angle correction ,Quadrant correction and gain correction is implemented. the angle correction is selected by the initial vector bits of selection and the System gain is controlled by an external gain control mechanism of fixed system gain similar to the Normal cordic implementation.

Keywords

CORDIC algorithm, rotation mode and vector mode, control CORDIC.

INTRODUCTION

THE Coordinate Rotation DIgital Computer (CORDIC) algorithm [1], [2] has been used for many years for efficient implementation of vector rotation operations in hardware. It is executed merely by table look-up, shift, and addition operations. Thus, the corresponding hardware can be implemented in very economic fashion. Subsequently, it has been applied for many performance demanding applications in digital signal processing (DSP), image processing, and video technology like fast Fourier transform (FFT) [3], [4], discrete Hartley transform (DHT) [4], [5], discrete cosine transform (DCT) [4], [6], discrete sine transform (DST) [4], Hough transform (HT) [7]–[9], [12], graphics application [10], [11], and motion vector estimation[12]. In essence, a CORDIC can be operated in two different modes: the rotation and the vectoring mode. In the former mode of operation, given a vector with initial coordinate (xo,yo) and a target rotation angle zo the objective is to compute the final coordinate(x1,y1) through a series of backward and forward rotation of the vector in an iterative manner. Digital signal processing (DSP) algorithms exhibit an increasing need for the efficient implementation of complex arithmetic operations. The computation of trigonometric functions, coordinate transformations or rotations of complex valued phasors is almost naturally involved with modern DSP algorithms. Popular application examples are algorithms used in digital communication technology and in adaptive signal processing. While in digital communications, the straightforward evaluation of the cited functions is important, numerous matrix based adaptive signal processing algorithms require the solution of systems of linear equations, QR factorization or the computation of Eigen values, eigenvectors or singular values. All these tasks can be efficiently implemented using processing elements performing vector rotations.

The Coordinate Rotation Digital Computer algorithm (CORDIC) gives the opportunity to calculate the desired functions in rather simple, and elegant way. CORDIC is a method for computing elementary functions using minimal hardware such as shift’s, adds/subs and compares. CORDIC works by rotating the coordinate system through constant angles until the angle is reduces to zero. The angle offsets are selected such that the operations on X and Y are only shifts and adds.

All trigonometric functions can be computed using vector rotation. The CORDIC algorithm was developed by Volder in 1959. It rotates the vector, step by step, with a given angle. Additional theoretical work has been done by Walther in 1971. The main principle of CORDIC are calculations based on shift registers and adders instead of multiplications, what saves much hardware resources. CORDIC is used for polar to rectangular and rectangular to polar conversions and also for calculation of trigonometric functions, vector magnitude and in some transformations, like discrete Fourier transform (DFT) or discrete cosine transform (DCT). In particular case, the CORDIC algorithm is used in wireless LAN (WLAN) by receivers.

CORDIC ALGORITHM

All the trigonometric functions can be computed or derived from functions using vector rotations. The CORDIC algorithm provides an iterative method of performing vector rotations by arbitrary angles using only shift and add operations. The algorithm is derived using the general rotation transform.

The CORDIC algorithm performs a planar rotation. Graphicall y, planar rotation means transforming a vector (Xi, Yi) into a new vector (Xj, Yj).

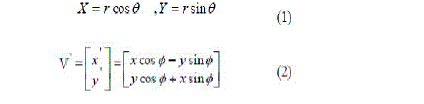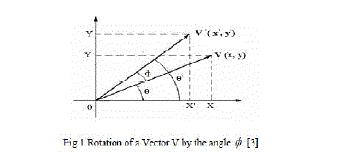V came into picture after anticlockwise rotation by an angle Ãâ¡ÃÂ¾ . From Fig.1, it can be observed

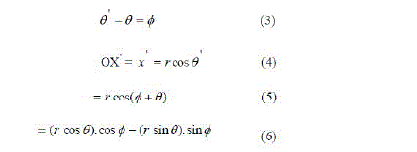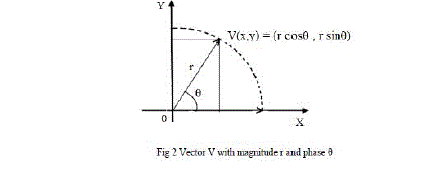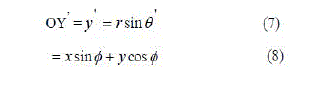VÃÅ½Ãâ after anticlockwise rotation of vector V by angle Ãâ¡ÃÂ¾ is

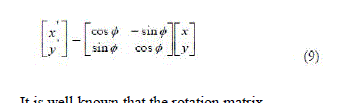It is well known that the rotation matrix

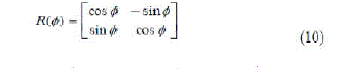in a program-like style:

For n=0 to [inf]

If (Z(n) >= 0) then

Z(n + 1) := Z(n) – atan(1/2^n);

Else

Z(n + 1) := Z(n) + atan(1/2^n);

End if;

End for;

In CORDIC processing, a bulk scale factor is generated that needs to be compensated. As long as all of the iterations allowed by a certain word length are carried out, the scale factor remains a constant and can be compensated with minimal hardware. However, in principle, the vector rotation for the majority of the angles lying in the coordinate space can be carried out using a smaller number of iterations by optimally choosing appropriate elementary rotation steps. This essentially requires by passing or repeating some of the CORDIC iterations as was proposed in [13] and [25]. However, in such a case, the scale factor no longer remains constant or predictable. The situation is much worse when the CORDIC works in an embedded system where other circuitry of that system (a typical example is an OFDM synchronizer for IEEE 802.11(a) standard [15]) generates data and supplies it to the CORDIC. In such a case, the CORDIC has no a priori information about the actual angle of rotation and, hence, the scale factor is completely unpredictable. For its compensation, hardware circuitry is needed that is as complex as the original CORDIC itself. To the best of our knowledge, there is no existing scheme reported to date that can keep the scale factor constant and predictable while at the same time adaptively executing the minimum number of elementary rotation steps However, the former approach results in an overhead in hardware while the latter increases the total number of CORDIC iterations.

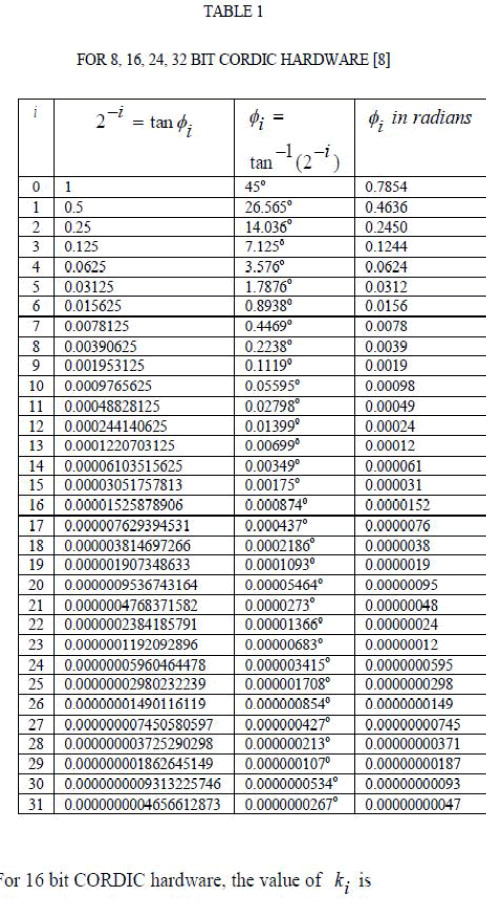
The architecture of the new CORDIC rotator can be derived by a suitable hardware mapping of the algorithm described above. For sake of clarity, the implementation of a 16-bit CORDIC rotator is described here as an example. All of the discussions presented in this section can be generalized for an n- bit CORDIC rotator as well.

The atan(1/2^i) is pre-calculated and stored in a table. [inf] is replaced with the required number of iterations, which is about 1 iteration per bit (16 iterations yield a 16bit result).

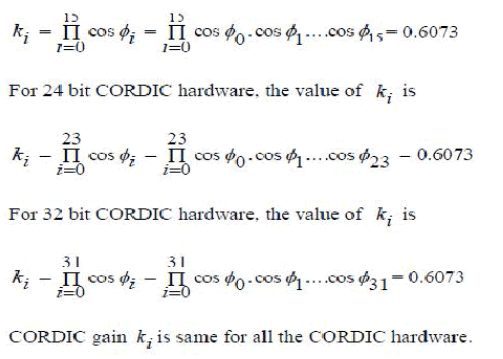SCALING OPTIMIZATION AND IMPLEMENTATION

Optimized set of angle rotations and micro-rotations are discussed in this section

A. Fixed Rotation Angle scaling approach

The normalized equation for the scale-factor given by (2) can be articulated explicitly for the set of selected m1 micro rotations as

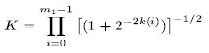where k(i) for 0≤i<m is the no. of shifts in the ith micro-rotation. Except for k(i)=0 (i.e., rotation by 45), by binomial expansion, any term can be written as

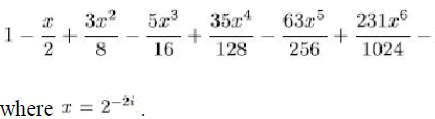SCALING IMPLEMENTATION FOR CORDIC

Micro-rotations and Scaling implemented either in the same circuit in interleaved manner or in two individual stages. The realization of scaling as well as the micro-rotation would however depend on desired level of accuracy, and the realization of scaling also depends on the realization of micro-rotations. Therefore, we discuss here the implementation of the scaling circuits with respect to different implementations of micro-rotations.

Computing Sine and Cosine functions

Sine and Cosine can be calculated using the first CORDIC scheme which calculates:

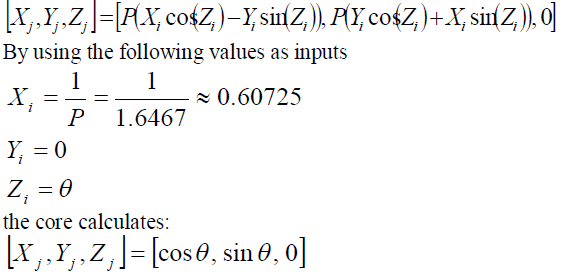The input Z takes values from –180degrees to +180 degrees where:

0x8000 = –180degrees

0xEFFF = +80degrees

But the core only converges in the range –90degrees to +90degrees.

The other inputs and the outputs are all in the range of –1 to +1. The congregate constant P represented in this format results in:

Example:

Calculate sine and cosine of 30degrees.

First the angle has to be calculated:

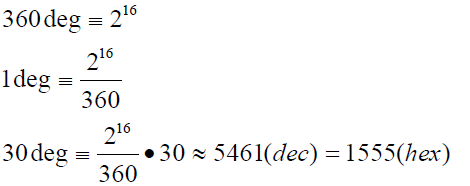The core calculates the following sine and cosine values for Zi=5461:

Sin : 16380(dec) = 3FFC(hex)

Cos : 28381(dec) = 6EDD(hex)q

The outputs represent values in the –1 to +1 range. The results can be derived as follows:

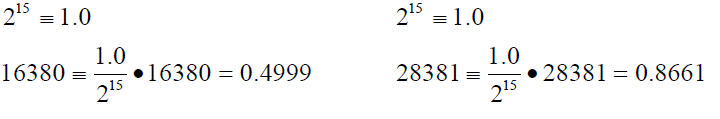Where as the result should have been 0.5 and 0.8660.

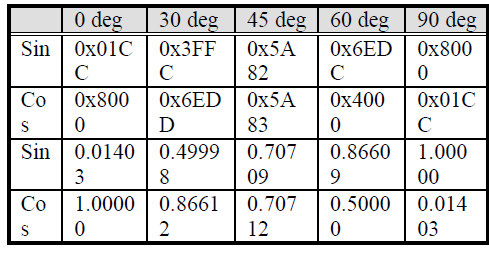
Table 1: Sin/Cos outputs for some common angle

Although the core is very accurate small errors can be introduced by the algorithm (see example and results table). This should be only a problem when using the core over the entire output range, because the difference between +1 (0x7FFF) and –1 (0x8000) is only 1bit.

Generalized Implementation of Scaling

The shift and add circuits for scaling with respect to (7) is shown. The scaling circuit of Shift and add scaling circuit by hardwired pre-shifted loading can use hardwired pre-shifting for minimizing barrel-shifter difficulty and could be located after the CORDIC cell of Fig. 2 to perform micro-rotation and scaling in two separate stages. The generalized CORDIC circuit for fixed rotation to perform the micro-rotation and the scaling in interleaved manner in alternate cycles is shown. The circuit of Fig. 8 is similar to that of Fig. It involves only an additional line-changer circuit to change the path of unshifted (direct) input.

BI ROTATIONAL CORDIC

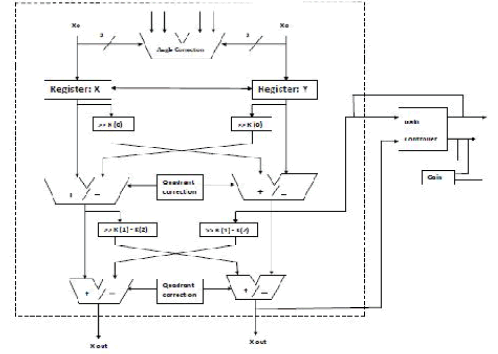For Reducing Errors in Quadrant, angle and Gain correction Bi rotational Cordic is one of the techniques with extra hard ware implementation predefined gain and Quadrant correctional algorithms these are implemented form the basic cordic theory for the more accuracy in gain .The angle range should be -90 to +90 and all angles should be in the rage of first and fourth Quadrant of rotational implementation. These blocks improves the cordic fixe4d rotation with more accuracy .The accuracy can also be improved by the more no of shifting stages. also.

COMPLEXITY CONSIDERATIONS

We discuss here the hardware and time complexity of the proposed design. In the presented text we do not find similar work on CORDIC realization of known and fixed rotations. Therefore, we compare the proposed design with the conventional CORDIC design for the rotation of unknown angle. We have used the basic CORDIC processor in [3, Fig. 2] for the realization of conventional CORDIC. In addition, we have designed a reference architecture (see Fig. 1) for straight forward implementation of fixed rotations, and we have compared the complexities and speed performance of the proposed design with the conventional and reference design.

RESULTS AND ANALYSIS

RTL Schematic of Cordic algorithm

Technology Schematic of Cordic algorithm

Simulation Results of Cordic algorithm

CONCLUSION

In this paper Control on BI CORDIC is implemented with Angle correction and Quadrant corrections .Accuracy can be further increased by these CORDIC algorithm techniques. Overshoot problem in original CORDIC has been overcome by angle selection scheme. Due to the increasing of no. of bits complexity of hardware also increases, which results in accurate simulation results.

References

Volder J. E,”The CORDIC trigonometric computing technique”, IRE Trans. Electronic Computing, Volume EC-8, pp 330 - 334, 1959.
Terence K. Rodrigues and Eari E.Swartzlander ,Jr.Fellow,”Adaptive CORDIC :Using parallel Angle Recoding to Accelerate Rotations”, IEEE Transactions on Computers, Vol .59,NO.4, April 2010
Pramod K.Meher, Senior Member ,IEEE, Javier Valls, Member, IEEE, Tso- Bing Juang , Member, IEEE, K.Sridhan, Senior Member, IEEE, and Koushik Maharatna, Member , IEEE “ 50 Years of CORDIC: Algorithms, Architectures, and Applications” , IEEE transactions on circuits and systems,VOL.56.NO.9,September, 2009.
Alan Sultan, “ CORDIC: How Hand calculators Calculate” Integre Technical Publishing Co.,Inc. college Mathematics journal VOL.40 NO.2 , March 2009.
Yu Hen Hu “CORDIC-Based VLSI Architectures for Digital signal processing”, IEEE Signal processing-1053-5888/92/$3.00, 1992.
Dr. Dobbs , Michael Pascale, “Using CORDIC methods for Computations in micro-controllers” ,1 September 2000.
Y.H .Hu, “CORDIC based VLSI architecture for digital signal processing”,IEEE signal processing Mag., pp 16-35, july 1992.
Kia Bazargan , “CORDIC Algorithms” EE-5324-VLSI Design 2, University of Minnesto,Spring 2006.
Tanya Vladimirova and Hans Tiggler,“FPGA implementation of sine and cosine generators Using the CORDIC Algorithm” surrey space centre ,University of Surrey , Guildford , Surrey , GU2 5XH.
Eric Keller,“Dynamic circuit specialization of CORDIC processor”, Nov 7, 2000.
Quiang Gao, “Low complexity Arithmetic Implementation for DSP Radio Receiver” university of strathcyclde.(qiang.gao@eee.strath.ac.uk).
Jean Duprat and Jean – Michel Muller “ The CORDIC Algorithm :New Results for Fast VLSI implementation” IEEE Transactions on computers ,Vol 42.No.2,Feb 1993.