Keywords
|
| the Kogge-Stone, Sparse Kogge-Stone, Spanning tree adder, Brent-kung adder, FPGA |
INTRODUCTION
|
| The binary adder is the critical element in most digital circuit designs including digital signal processors (DSP) and microprocessor data path units. As such, extensive research continues to be focused on improving the power delay performance of the adder. In VLSI implementations, parallel-prefix adders are known to have the best performance. Reconfigurable logic such as FieldProgrammable Gate Arrays (FPGAs) has been gaining in popularity in recent years because it offers improved performance in terms of speed and power over DSP-based and microprocessor-based solutions for many practical designs involving mobile DSP and telecommunications applications and a significant reduction in development time and cost over Application Specific Integrated Circuit (ASIC) designs. The power advantage is especially important with the growing popularity of mobile and portable electronics, which make extensive use of DSP functions. However, because of the structure of the configurable logic and routing resources in FPGAs, parallel-prefix adders will have a different performance than VLSI implementations. In particular, most modern FPGAs employ a fast-carry chain which optimizes the carry path for the simple Ripple Carry Adder (RCA). In this paper, the practical issues involved in designing and implementing tree-based adders on FPGAs are described. An efficient testing strategy for evaluating the performance of these adders is discussed. Several tree-based adder structures are implemented and characterized on a FPGA and compared with the Ripple Carry Adder (RCA) and the Carry Skip Adder (CSA). Finally, some conclusions and suggestions for improving FPGA designs to enable better treebased adder performance are given. |
RELATED WORK
|
| On the Xilinx 4000 series FPGAs, the ripple carry adder and carry-skip adders, only an optimized form of the carryskip adder performance is more better than the ripple carry adder when the adder operands were above 56 bits. A study of adders yielded similar results when implemented on the Xilinx t II. In the authors considered several parallel prefix adders implemented on a Xilinx Virtex 5 FPGA. It is found that the normal RCA adder is superior to the parallel prefix designs because the RCA can take advantage of the fast carry chain.This study focuses on carry-tree adders implemented on a FPGA of Xilinx Spartan 3E. The distinctive contributions of this paper are two-folded. In the first, we consider tree-based adders and a hybrid form which combines a tree structure with a ripple-carry design. The Kogge-Stone adder is taken as a representative of the former type and the Modified Kogge-StoneAdder is the representative of the latter category. Second, this paper considers the practical issues involved in testing the adders and provides actual measurement data to compare with simulation results. In addition with being able to compare the simulation data with measured data using a high-speed logic analyzer, our results present a different perspective in terms of both results and types of adders. |
| The adders to be studied were designed with varied bit widths up to 128 bits and coded in VHDL. The Xilinx ISE 10.1i software was used to synthesize the designs onto the Spartan 3E FPGA.By seeing the synthesis reports of both Kogge- Stone Adder and Modified Kogge-Stone Adder,the results are same for both adders even if we reduce the black cells in Modified Kogge-Stone Adder.That is we reduced the space for implementation of adder. |
CARRY TREE ADDERS DESIGNS
|
| High performance adders, also known as carry-tree adders, pre-compute the propagate and generate signals. In tree adders, carries are generated in parallel and fast computation is obtained at the expense of increased area and power. The main advantage of the design is that the carry tree reduces the number of logic levels (N) by essentially generating the carries in parallel. |
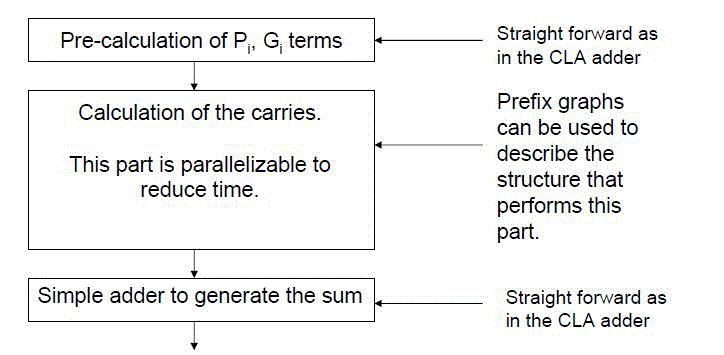
| The parallel-prefix tree adders are more favorable in terms of speed due to the complexity O(log2N) delay through the carry path compared to that of other adders. The prominent parallel prefix tree adders are Kogge-Stone, Brent-Kung, Han-Carlson, and Sklansky.it was found from the literature that Kogge-stone adder is the fastest adder when compared to other adders. The adder priority in terms of worst-case delay is found to be Ripple-Carry, Carry-Look-Ahead, Carry- Select and Kogge-Stone. This is due to the number of “Reduced stages”. Kogge-Stone adder implementation is the most straightforward, and also it has one of the shortest critical paths of all tree adders. The drawback with the Kogge- Stone adder implementation is the large area consumed and the more complex routing (Fan-Out) of interconnects. A Parallel Prefix Adder (PPA) is equivalent tothe CLA adder.The two different in the way their carry generation block isimplemented. The parallel prefix carry look ahead adder wasfirst proposed some twenty years ago as a means ofaccelerating n-bit addition in VLSI technology. It widelyconsidered as the fastest adder and used for high performancearithmetic circuits in the industries. A three step process isgenerally involved in the construction of a Parallel PrefixAdder. The first step involves the creation of generate andpropagate signals for the input operand bits. The second stepinvolves the generation of carry signals. In the final step, the sum bits of the adder following stagesof the operand bits and the preceding stage carry bit using a xor gate. |
| 1. Pre-processing stage. |
| 2. Carry look ahead stage. |
| 3. Post processing stage. |
Preprocessing
|
| This step involves computation of generate and propagate signals corresponding to each pair of bits in A and B. |
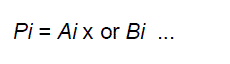 |
| Gi = Ai and Bi ... |
Carry Generation Network
|
| In this stage we compute carries corresponding to each bit. Execution of these operations is carried out in parallel. After the computation of carries in parallel they are segmented into smaller pieces. It uses carry propagate and generate as intermediate signals which are given by the logic Equations (3 and 4) |
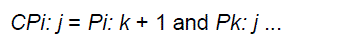 (3) (3) |
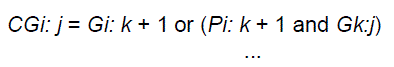 (4) (4) |
Post Processing
|
| This is the final step and is common to all adders of this family (carry look ahead). It involves computation of sum bits. |
 (5) (5) |
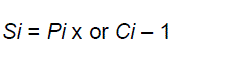 (6) (6) |
DIFFERENT TYPES OF PARALLEL PREFIX ADDERS
|
1.Kogge-stone adder
|
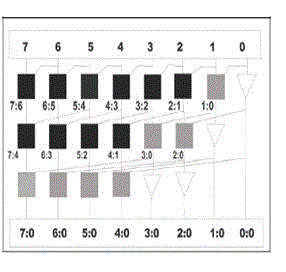
| The Kogge-Stone adder is a parallel prefix form of carry look-ahead adder. It generates the carry signals in O (log2N) time, and is widely considered as the fastest adder design possible. It is the most common architecture for highperformance adders in industry. The Kogge-Stone adder concept was first developed by Peter M. Kogge and Harold S. Stone. In Kogge-stone adder, carries are generated fast by computing them in parallel at the cost of increased area. Tree structures of carry propagate and generate signals in 8-bit Kogge-Stone Adder (KSA) is shown in Figure 1. Carry generation network is the most important block in tree adders, and it consists of three components such as Black cell, Grey cell and Buffer. Black cells are used in the computation of both generate and propagate signals. Gray cells are used in the computation of generate signals which are needed in the computation of sum in the post-processing stage. Buffers are used to balance the loading effect. |
2.Modified Kogge-Stone Adder
|
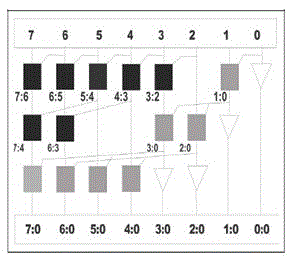
| The Kogge-Stone adder in Figure 1 is faster than other well known parallel prefix adders and has fan-out of 2 in all stages. We can reduce the computation by eliminating the redundant cells thus compensating for the increased delay. The Kogge-Stone adder can be modified by reducing the Black cells and rerouting to compensate the functionality of adder. Propagate-Generate (PG) network of modified 8-bit Kogge-stone adder is shown in Figure 2. Delay of the Kogge-Stone adder can also be decreased by only rerouting the wires but this is not so effective because area remains same. We can increase the speed of adder also by eliminating redundant Black cells which results in reduction in area of the adder. |
3.Routing Technique
|
| The one important concept in all tree adders is that each cell has its own task in the overall output, for example in the second stage of the 8-bit Kogge-Stone adder on the left the generate bit is calculated if only bit-6 and -7 is present. It only requires generate bit from bit-0 to -5, when these two generate bits are combined it gives the generate bit for the overall bit-0 to -7. The important concept is that generate bit of 6 and 7 need generate bits from the calculation of bit 0 to 5 but instead, can give it the generate bit calculated using bit 0 to 6 and will obtain the same result. This is because generate bit from 6 is already included but is being added again from the computation of generate bit of 0 to 6 and this does not affect the end result. But final generate bit from bit-i cannot take any generate bits higher than i, if so the end result will be affected as we are included the generate value of the higher bits. The above mentioned method is a good start but we can even take it a step further by trying to remove some of the redundant cells. Redundant cells can be removed without any adverse consequences but it has to be properly compensated, if not the delay will increase considerably. And this can be compensated by changing the routing (wiring).Performing the rerouting in only first and the second stages produced an improvement in speed but doing the same in all 3 stages of carry-generate network increases delay. |
| IMPLEMENTATION |
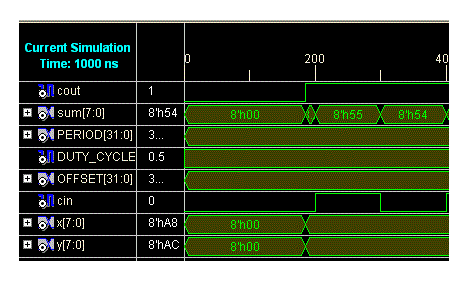
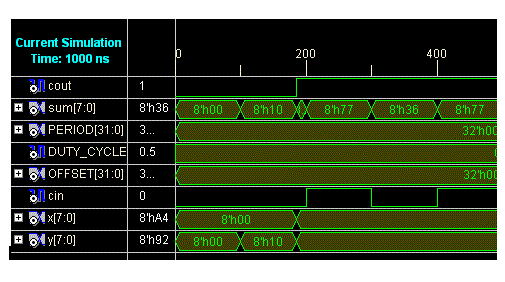
| The design of different tree adders are coded in Verilog Hardware Description Language using structural modeling in Xilinx ISE Design Suite 10.1i and all the simulation results are taken using XILINX ISIM simulator. Synthesized for the Spartan-3 FPGA XC3S400 with the speed grade of 4.In the simulation process of kogge stone adder, x=A8 h and y=AC h of 8 bits are taken as inputs and sum=54 h and cout=1 are taken as outputs. In the simulation process of Modified Kogge-Stone Adder x=A4h and y=92 h are taken as inputs and sum=36 hand cout=1 are taken as outputs.However,both adders performs the correct addition operation but the only change is the Modified Kogge-Stone Adder requires less space that is less number of components. |
CONCLUSION
|
| This paper presents an innovative way of modifying the already existing Kogge-Stone adder by re-routing (wiring) and Black-cell reduction for increasing the speed of execution. The design originates from the principle of removing the redundant black cells and compensating this removed cells by rerouting. The above design has a delay which is much less than the architectures that it is being compared with. The number of logic levels used is also found to be less. |
Figures at a glance
|
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
|
References
|
- AhmetAkkas and Michael J Schult (2011), “A Decimal Floating-Point Fused Multiply-Add Unit with a Novel Decimal Leading-Zero Anticipator”, AMD IEEE.
- Anitha R and BagyaveereswaranV(2012), “High Performance Parallel Prefix Adders with Fast Carry Chain Logic”,International Journal ofVLSI Design &Communication Systems, Vol. 3, No. 2,pp. 01-10, ISSN 0976-6499.
- David Jeff Jackson and Sidney Joel Hannah (1993), “Modeling and Comparison of Adder Designs with Verilog HDL”, 25th South-Eastern Symposium on System Theory, March, pp. 406-410.
- Kogge P and Stone H (1973), “A Parallel Algorithm for the Efficient Solution of a General Class of Recurrence Relations”, IEEE Transactionson Computers, Vol. C-22, No. 8, pp. 786-793.
- Krishna Kumari V, Sri Chakrapani Y and Kamaraju M (2013), “Design and Characterization of Koggestone, Sparse Koggestone, Spanning Tree and Brentkung Adders”, International Journalof Scientific & Engineering Research, Vol. 4, No. 10, pp. 1502-1506, ISSN 2229-5518.
- Madhu Thakur and Javed Ashraf (2012),“Design of Braun Multiplier with Kogge-Stone Adder & It’s Implementation on FPGA”, International Journal of Scientific& Engineering Research, Vol. 3, No. 10,pp. 03-06, ISSN 2229-5518.
- NurdianiZamhari, Peter Voon, KuryatiKipli, Kho Lee Chin and MaimunHujaHusin (2012), “Comparison of Parallel Prefix Adder (PPA)”, Proceedings of the World Congress on Engineering, WCE, Vol. 2, July 4-6, London, UK.
- PakkiraiahChakali and Madhu Kumar Patnala (2013), “Design of High Speed Kogge-Stone Based Carry Select Adder”, International JournalofEmergingScience and Engineering (IJESE), Vol. 1, No. 4, ISSN: 2319-6378.
- Weste Neil, Harris David and BanerjeeAyan (2009), “CMOS VLSI Design: A Circuits and System
|