ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| P.Thamarai1, B.Karthik2 , Dr. T.V.U.Kirankumar3 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This paper addresses the joint transmit and receive optimization and linear processing for multiuser multiple-input, multiple output (MIMO) downlink. Each user may receive multiple data streams. Our design is to maximize the sum throughput under power constraint is equivalent to minimizing the product of mean square error matrix determinants(PDetMSE).Other one is to minimize the total transmit power with sum rate requirement. A scalar version of mean square error is considered to solve the problem. The problem is product of mean square error does not provide efficient solution. Once the optimal structure of the transmit-receive processing is known, the design problem simplifies and can be formulated within the powerful framework of convex optimization theory, in which a great number of interesting design criteria can be easily accommodated and efficiently solved even though closed-form expressions may not exist. we devise iterative algorithm where each iteration contains the optimization of uplink power, uplink receive filter, downlink receive filter. For these problem a new power allocation schemes are derived, which can be devised as Differential evolution(DE) involving mean square error. Simulations show that proposed algorithm are proved to be convergent and outperform existing linear methods.
Keywords |
| Multiuser MIMO systems, transceiver design, sum-rate maximization , Differential evolution algrothim |
INTRODUCTION |
| THE benefits of using multiple antennas for wireless communication systems are well known. When antenna arrays are present at the transmitter and/or receiver, multiple input, multiple-output (MIMO) techniques can utilize the spatial dimension to yield improved reliability, increased data rates, and the spatial separation of users. In this paper, the methods we propose will focus on exploiting all of these features, with the goal of maximizing the sum data rate achieved in the MIMO multiuser downlink.The achievable capacity region of multiuser MIMO broadcast channels is characterized in an information theoretic context, e.g., [1], [2]. Schemes under the assumption of 'dirty paper precoding' were proposed in [3], . The sum-rate optimality of DPC was generalized to an arbitrary number of multi antenna receivers using the notions of game theory and uplink-downlink duality [4]; this duality is employed in[5] to derive iterative solutions that find the sum capacity.DPC precoding strategy has proven to be a difficult problem. |
| Existing solutions, which are largely based on Tomlinson-Harashima precoding (THP) [6], incur high complexity due to their nonlinear nature and the combinatorial problem of user order selection.Linear precoding provides an alternative approach for transmission in the MIMO downlink, trading off a reduction in precoder complexity for suboptimal performance. Orthogonalization based schemes use zero forcing (ZF) and block diagonalization (BD) to transform the multiuser downlink into parallel single-user systems.Thus, zero-forcing is not a capacity-achieving strategy. A water filling power allocation can then be used to allocate powers to each of the users [7]. It is also possible to improve the sum rate achieved with ZF and BD by including user or antenna selection in the precoder design. In this paper, we consider the optimal formulation for sum rate maximization under linear precoding. Much of the existing literature on linear precoding for multiuser MIMO systems focuses on minimizing the sum of mean squared errors (SMSE) between the transmitted and received signals under a sum power constraint [8]–[9]. An important recurring theme in most of these papers is the use of an uplink-downlink duality for both MSE and signal-to interference-plus-noise ratio (SINR) introduced in [10] for the single receive antenna case and extended to the MIMO case in [11]. |
| Linear precoding approaches an iterative method for direct optimization of the sum rate, while [13] and [14] exploit the SINR uplink-downlink duality of [10], [11]. In [16][17] two similar algorithms were independently proposed to minimize the product of the mean squared errors (PMSE) in the multiuser MIMO downlink; these papers showed that the PMSE minimization problem is equivalent to the direct sum rate maximization proposed in [14]. The work of [15] was motivated by the equivalence relationship developed between the single user minimum MSE (MMSE) and mutual information in [18]. Each of the approaches in [12] yields a suboptimal solution, as the resulting solutions converge only to a local optimum, if at all. |
| It has been shown that with linear processing the above problems are non-convex, thus known algorithms for determinant maximization can not be applied[19]. Here, we propose iterative algorithms to jointly optimize the transmit powers, transmit and receive filters, which are suitable for both uplink and downlink transmission, based on the uplink/downlink duality[20]. |
| Notation: Lower case italics, e.g., x, represent scalars while lower case boldface type is used for vectors (e.g., x). Upper case italics, e.g., N , are used for constants and upper case boldface represents matrices, e.g., X. Entries in vectors and matrices are denoted as [x]i and [X]i,jrespectively. The superscripts T and H denote the transpose and Hermitian operators. E[.] represents the statistical expectation operator while IN is the Nïÿýïÿý.N identity matrix. tr [.] and det are the trace and determinant operators. x 1 and x 2 denote the 1- norm (sum of entries) and Euclidean norm. diag(x) represents the diagonal matrix formed using the entries in vector x. |
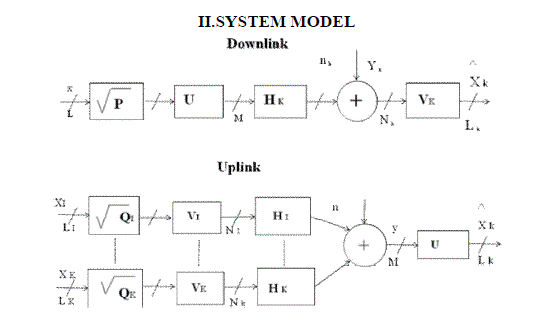 |
 |
 |
 |
 |
IV.DE ALGORTHIM |
| The DE algorithm is a population based algorithm like genetic algorithms using the similar operators; crossover, mutation and selection. The main difference in constructing better solutions is that genetic algorithms rely on crossover while DE relies on mutation operation. This main operation is based on the differences of randomly sampled pairs of solutions in the population. The algorithm uses mutation operation as a search mechanism and selection operation to direct the search toward the prospective regions in the search space. The DE algorithm also uses a non-uniform crossover that can take child vector parameters from one parent more often than it does from others. By using the components of the existing population members to construct trial vectors, the recombination (crossover) operator efficiently shuffles information about successful combinations, enabling the search for a better solution space. |
| An optimization task consisting of D parameters can be represented by a D-dimensional vector. In DE, a population of NP solution vectors is randomly created at the start. This population is successfully improved by applying mutation, crossover and selection operators. |
| The main steps of the DE algorithm is given below: |
| a. Initialization |
| b. Evaluation |
| c. Repeat |
| d. Mutation |
| e. Selection |
| f. Until the required accuracy met |
 |
V.SIMULATION RESULTS |
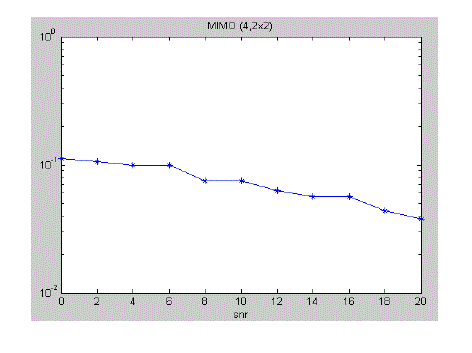
| The PMSE and PDetMSE algorithms do not require the explicit selection of Nd; rather, this parameter is determined implicitly by the power allocation. However, we can force the PMSE algorithm to allocate a maximum number of substreams Nd to each user to gain further insight into its behaviour. In Fig. 5, the number of streams in the Nd = 4 system described below is varied from x1 = x2 = 2 to x1 = 3 and x2 = 1. The achievable sum rate in this system decreases in the latter case, as the asymmetric stream allocation does not correspond to the symmetric channel configuration |
 |
 |
| In this case, user 2 is restricted to only a single data stream, and thus can not take full advantage of good channel realizations. If the goal is always, maximizing the sum rate, the users should be allocated the maximum number of data streams in as balanced a manner as possible. |
VI.CONCLUSIONS |
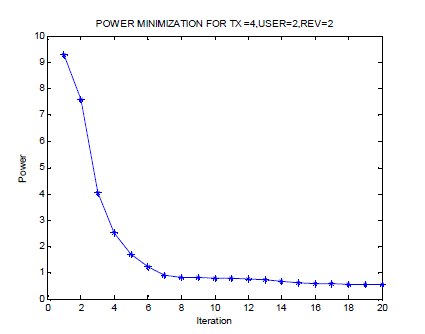
| we have considered the problem of designing a linear precoder to maximize sum throughput in the multiuser MIMO downlink under a sum power constraint. We have compared the maximum achievable sum rate performance of linear precoding schemes to the sum capacity in the general MIMO downlink. The problem was reformulated in terms of MSE based expressions, and the joint processing solution based on PDetMSE minimization was shown to be theoretically optimal, but computationally infeasible. A suboptimal framework based on scalar processing was then proposed, and an implementation was provided based on PMSE minimization We propose iterative algorithms based on MSE duality and Differential evolution. Unlike the power control by DE with respect to SINR, we propose a new power control strategy by optimizing geometric MSE together with MMSE estimation. The algorithms are proved to be convergent. |
References |
|