Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Designing a Human Mobility Model Based Routing Protocol for Delay Tolerant Network (DTN)

Ponsundari.S1, Siva Ganesh.E2
  1. PG Student, Department of CSE, Einstein College of Engineering, Tirunelveli, Tamilnadu, India
  2. Assistant Professor, CSE Department, Einstein College of Engineering, Tirunelveli, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Understanding human mobility is critical for simulations of mobile devices in a wireless network, but current mobility models often do not reflect real user movements. The common human mobility model that satisfies following fundamental statistical features:1) Heavy-tail flight and pause-time distributions; 2) Heterogeneously bounded mobility areas of individuals; 3)Truncated power-law intercontact times; 4)The destinations of people (or we say waypoints) are dispersed in a self-similar manner; and 5) People are more likely to choose a destination closer to its current waypoint. These features are known to be influential to the performance of human-assisted mobility networks. The main contribution of this paper is to present a new mobility model that can produces synthetic mobility traces containing all the five statistical features in various mobility settings. It brings out the unique performance features of various routing protocols.



 

Keywords
Human Mobility, Delay Tolerant Network, Mobile Network, Levy Walk, Mobility Model.

INTRODUCTION
The purpose of mobile computing and communications is to allow people to move about and yet be able to interact with information, services, and other people. Anyone designing an application [1], system, or network to serve mobile users must therefore have some notion about how the users, and their devices, move. The increasing popularity of devices equipped with wireless network interfaces (such as cell phones or PDAs) offers new communication services opportunities. Such mobile devices can transfer data in two ways - transmitting over a wireless (or wired) network interface, and carrying from location to location by their user (while stored in the device). Communication services that rely on this type of data transfer will strongly depend on human mobility characteristics and on how often such transfer opportunities arise. Therefore, they will require fundamentally different networking protocols that are used in the Internet
The goal of developing a human mobility model that abstracts out many geographically specific details that might change from one setting to another, and that faithfully reproduces fundamental and invariant statistical properties of human mobility. Generally human mobility patterns are used in simulating mobile networks of wireless devices carried by people. As wireless devices are often attached to humans, understanding their mobility patterns leads to more realistic network simulation and more accurate understanding of protocol performance. The fundamental statistical properties of human mobility from real traces of human mobility such as GPS traces of human walks in various locations, cell-phone location tracking, recordings of wireless device associations with their access points , and tracking of bank notes. Commonly, human mobility model that satisfies following property from (F1–F3) as well as two new features (F4–F5) are added in this paper.
F1) Heavy-tail flights and pause-times:
A flight is a Euclidean distance between two waypoints visited in succession by the same person in the same daily trip, and waypoints are the locations where a walker stops for longer than a certain period of time before moving again. Waypoints are intuitively considered as destinations where people stop their travel. Pause-time is the time duration that a person spends in a waypoint.
F2) Heterogeneously bounded mobility areas:
Peoples are mostly move only within their own confined areas of mobility and that different people may have widely different mobility areas.
F3) Truncated power-law intercontact times (ICTs):
The distribution of intercontact time that is, the time elapsed between two successive meetings of the same persons can also be modelled by a truncated power-law distribution which consists of a power-law head followed by an exponentially decaying tail after a certain characteristic time.
F4) Self-similar waypoints:
The waypoints of humans can be modelled by self-similar points. The self-similar dispersion of waypoints intuitively implies that people are always more attracted to more popular places, their visiting destinations tend to be heavily clustered, and such clustering patterns are persistent in various spatial scales.
F5) Least-Action Trip Planning (LATP):
The people are more likely to visit destinations nearer to their current waypoint when visiting multiple destinations in succession.
All these properties (F1–F5) are intrinsically related to each other. The peoples are planning their daily trips using LATP (F5) on top of self-similar waypoints (F4) produce heavy-tail flight patterns (F1). It is shown that heavytail flights within a confined area (F2) result in truncated power-law ICTs (F3). Note that self-similar waypoints and power-law flight distributions are related, but not necessarily equivalent.

RELATED WORK
Many Biologists have found that the mobility patterns of foraging animals such as spider monkey, albatrosses (seabirds) and jackals can be commonly described as Levy Walk [2]. The term levy walk is to explain atypical particle diffusion not governed by Brownian motion (BM).BM characterizes the diffusion of tiny particles with mean free path and a mean pause time flights. A flight is defined to be a longest straight trip from one location to another that a particle makes without a directional change or pause. Commonly used mobility models include random way point (RWP) or random walk models such as Brownian motion and Markovian mobility. These models are simple enough for theoretical analysis and experimental simulation.
In this paper, we study the statistical patterns of human walks observed within a radius of tens of kilometres. We use mobility track logs obtained from 44 participants carrying GPS receivers for one month period. The sample traces are obtained from university campuses, one metropolitan area, and one theme park. The participants walk most of times in these locations and may also occasionally travel by bus, trolley, cars, or subway trains.
From the data analysis of our traces, we find the followings:
? The mobility patterns of the participants in these outdoor settings have features defining Levy walks; their flight distributions and pause time distributions closely match truncated power-law distributions. Their MSD also shows significant influence of these mobility patterns.
? There exist some deviations from pure Levy walks occurring due to various factors specific to human mobility including geographical constraints such as roads, buildings, obstacles and traffic. These deviations are manifested in our traces in the form of flight truncations which may make the flight distribution appear like heavy-tailed or even short-tailed at times.
From these findings, we construct a simple Levy walk (LW) mobility model that can be used for network simulation. LW is shown to be versatile enough to emulate various statistical features and those deviations observed in our traces when run under similar geographical constraints.
Table I shows four categories of existing models. RWP, Random Direction (RD), BM, or Random Walk (RW) and TLW [1] are pure random mobility models. In pure random mobility, each waypoint is chosen randomly based on some probability distribution. The Markovian Waypoint (MWP) [12] and Gauss–Markov (GM) model [11] are variants of the above, as they implement some Markovian transition probabilities among waypoints or prohibit unrealistic abrupt velocity changes. In RPGM [13], mobile nodes form several groups, each of which contains one leader. The leader moves according to the RWP, and all other members of a group move along their leader. Other models consider geographical constraints or social contexts and collective behaviours. These models are based on the intuition that people are attracted to locations where socially close people are gathered around.

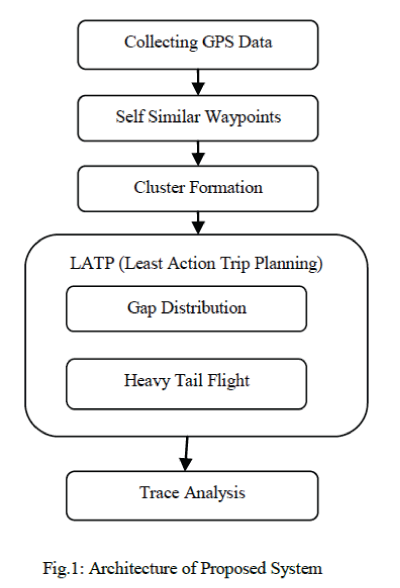
PROPOSED SYSTEM
In this work we develop a new human mobility model that satisfies all fundamental statistical features of self similar least action human walk. The self-similar waypoints intuitively implies that people are always more attracted to most popular places, their visiting destinations tend to more heavily clustered. Using those self similar waypoints we form a cluster.
A. GPS Data Set
The GPS receivers automatically record the people current positions at every 10s into a daily track log. The total numbers of traces from various locations are containing more than 200000 flight samples. The participant?s sites are randomly chosen to trace, while those moving from one location to another. The spatial resolution of human mobility traces are collected using Wi-Fi access points or cellular towers or base stations.
B. Self-Similar Waypoints
From the GPS data?s finding the self similar waypoint using Truncated Power Law (TPL). The power-law slopes of the heavy-tail flight distributions from our traces are different from one site to another.
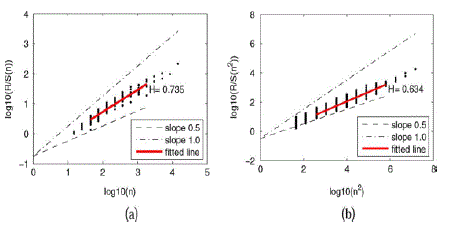
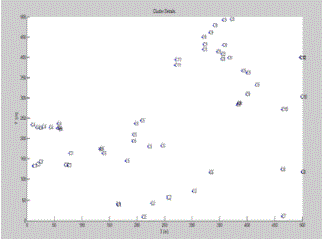
Formally, a stochastic process is called self similar or long-range-dependent if its auto-correlation function decays slowly. Intuitively, this slow decay indicates a high degree of correlation between distantly separated points of the process. Self-similarity is usually quantified by the Hurst parameter, and several methods for measuring this parameter from traces exist in literature [3]. We use two such well-known methods to quantify the self-similarity of the waypoint dispersion in our traces, namely the aggregated variance and the R/S methods. In the aggregated variance method, we divide the site map by a grid of unit squares (initially 5 ×5 m2), count all the waypoints within each unit square, and then normalize the count by the area of the unit square. Then, we measure the variance in these normalized count samples. If there exists long-range dependency in the samples, the aggregated variance should not decay faster than 1 in a log-log scale as we increase the size of the unit square. The Hurst parameter of the samples is defined to be1-β/2. The sample data are said to be self-similar if the Hurst parameter is in between 0.5 and 1. Aggregated variance can also be computed over one dimension by mapping waypoints. The Hurst parameter values measured from the aggregated variance test using the aggregated traces of each site over one dimensional and two-dimensional space.
In the R/S method, for a one-dimensional data set X= {Xi,,i ≥ 1} with partial sum Y(n)= ???? ???? =1 , the R/S statistic or the rescaled adjusted range, is given by
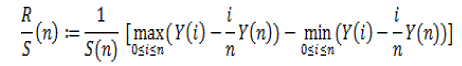image
Where S (n) is sample variance.
C. Gap Distributions
Flights are line trips over the waypoints. The order in which a walker visits the waypoints that determines flight patterns and relationship between self similar points and their corresponding gap distribution. Using Delaunay triangulation to measure the gap between similar points and identifies neighboring points. The complementary cumulative distributions (CCDF) of the length of flights are extracted from the same trace.
We first examine the relation between one-dimensional self similar points and their corresponding gap distribution, and later we generalize our analysis to two-dimensional cases through simulation. Consider a process dispersing a set of points over one-dimensional space. Let Y(x) be the number of points over a line interval (x and x+Δ). In other words, Y(x) is a point-count sequence over a small interval Δ. The self similarity of point counts Y(x) can be manifested in several equivalent ways. First, the aggregated variance v(m) of Y(x), which is a variance of a new series by averaging the original series Y(x) for non overlapping blocks consisting of m elements, replacing each block by its mean, has an asymptotic form of v(m) ~ m-β ,0<β<1 as m→ ∞. The Hurst parameter can be expressed as H=1-β/2. Second, the power spectrum S (f) of Y(x) has 1/f noise around the origin, that is, S (f) ~ f –?, 0<?<1 as f→0.The gap (interval) between two points can be measured as follows. We first make Δ small enough to hold at most one point and define the distance between any two immediately neighbouring points as gap. Let p(x) is the probability density function of a random variable „x? representing a gap among the self similar point process Y(x). The complementary cumulative distribution function (CCDF) of the length of triangle sides and flights extracted from the same trace. It is visually striking that the flight patterns and their corresponding distributions are very similar.
D. Relationship between Heavy-Tail Flights and Gaps Over Self-Similar Waypoints
Here we examine how gaps over self similar waypoints are related to heavy tail flights. The similarity between the gap and flight distributions suggests that there might be a connection between the sequence of visits to multiple destinations (i.e., waypoints) and gaps among self-similar points. They are more likely to visit nearby destinations before visiting farther destinations
E. Least-Action Trip Planning(LATP)
The similarity in the distributions of the gaps and flights suggests the order in which a walker visits for a given set of waypoints. Obviously, people are not conscious about gaps when they travel. This may imply that people tend to minimize the travelling distance. Intuitively, when people are to visit multiple destinations located at different distances, people often strive to minimize the total distance of travel.
In campus scenarios, people may have unexpected urgent events (e.g., appointments) that force them to make trips regardless of their travelling distances. The result indicates that LATP can recover almost identical flight distributions as the real ones from the traces and thus confirms that people use distance as an important factor in deciding the next destination of their trips.
We construct a new trip planning algorithm called LATP that, given a set of waypoints to visit, decides the order in which a person visits them. Algorithm 1 gives a pseudo code of LATP. The algorithm selects a next unvisited waypoint to visit based on a probability function P (c.v), which uses a weighted function 1/da (c,v). d (c,v) is the distance from the current waypoint „c? to an unvisited waypoint v , and a is a constant. If „a? is larger, then the algorithm is more likely to choose the nearer unvisited waypoint, and if it is zero, then it randomly chooses the next waypoint. LATP finishes when it visits all the unvisited waypoints. Visiting only unvisited waypoints is justified because waypoints are heavily clustered due to their self-similarity. People visiting the same hotspots repeatedly in a day are emulated by having them visit unvisited waypoints in close proximity to each other. This emulates repeated visits to the same hotspots because even if people visit the same hotspot repeatedly in a day, their exact GPS locations can be slightly different despite being in the same cluster.
image

METHODOLOGY
SLAW mainly takes two input parameters, a Hurst parameter value [1] and a weight on distance in performing LATP, along with other trace-specific information such as the size of the mobility areas and the number of mobile nodes. The Hurst parameter value determines the degree of self-similarity for waypoint dispersion. The weight factor for LATP [1] determines the likelihood of visiting nearby destinations when a node has multiple candidate destinations. Users of the model do not need to extract these parameter values from real traces. Instead, we provide the ranges of values for users to choose from for the parameters. For instance, the Hurst value must be in between 1/2 and 1 to ensure the self-similarity of waypoints. In the aggregated variance method [1], we divide the site map by a grid of unit squares (initially of 5*5 m2), count all the waypoints within each unit square, and then normalize the count by the area of the unit square. Then, we measure the variance in these normalized count samples.
To measure the impact of these mobility patterns on the performance of mobile network protocols, we study the performance of DTN routing under various mobility models, including SLAW. It captures the unique performance properties of many existing DTN routing protocols. More specifically, it provides a clear performance differentiation between stateless and stateful protocols where stateful protocols require and utilize past contact information among nodes to predict future contact probability and stateless protocols do not. SLAW induces more frequent and regular contacts among nodes that result in more predictable and shorter routing delays for those protocols. The applications of our work go beyond mobile networks. SLAW can be an important tool for emulating human walk behaviours in diverse application scenarios that can be applied to accurate urban planning, traffic forecasting and biological and mobile virus spread analysis.

RESULTS AND DISCUSSION
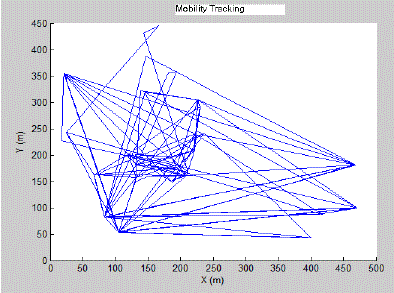
The human mobility model which takes an input arguments of distance alpha, number of users, area size, number of waypoints, Hurst parameter, total hours for tracking, clustering range, beta, minimum pause time and maximum pause time. Using those values generate a waypoint that is the location of each and every user. Then form a cluster that is grouping the user within the range of 30m. Also find the starting and destination of every user. Finally track the mobility of individual user. After completing mobility tracking finding the average delay value that depends on the clustering value.
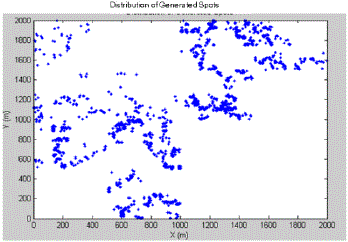
Fig.3 shows that generating waypoints in college campus using R/S method.
Fig.4 shows that forming a cluster that is grouping the user within the range of 30m depending on waypoints (location of the user).
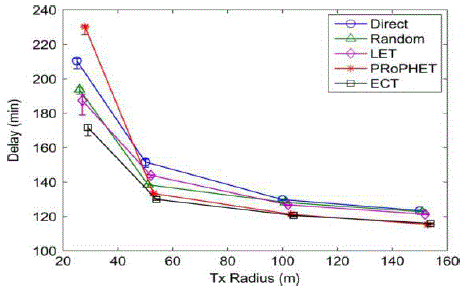
The implementation result illustrates that, the average routing delay varies depending on transmission area. We test the following five DTN routing protocols: Random forwarding [11], direct transmission [11], PRoPHET [12], Last Encounter Time (LET) [4], and Expected Contact Time (ECT). Note that all routing protocols are tested with the mobility traces generated from different mobility models. The GPS traces from [1] are individual traces that are not recorded at the same time. Thus, it is infeasible to test routing protocols over the traces.

CONCLUSION
In this paper, we present a new mobility model that captures the statistical features found in real human mobility traces. We report many pieces of both analytical and empirical evidence that the movement of people can be expressed very well using spatial gaps among fractal waypoints and present confirming data for the use of the leastaction principle in human trip planning. Based on this, we develop a simple heuristic algorithm called LATP that generates heavy-tail flights on top of fractal waypoints. Combining with heterogeneously bounded walk about areas, we can successfully reproduce many statistical features important to the study of mobile network performance, especially truncated power-law ICTs. Our routing performance study expresses mobility patterns arising from people with some common interests or within a single community like students in the same university campus or people in theme parks where people tend to share common gathering places. In some situation this type of mobility model does not captures temporal correlations. In future this type of models satisfies spatial and temporal features.

Tables at a glance
Table icon
Table 1

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
Figure 4 Figure 5 Figure 6

References