Determine the Post-Construction Settlement of the Embankment and Its Foundation for the Lom Pangar Dam in Cameroon

Abstract

This paper has as purpose to show the calculations done to determine the settlement of the embankment and its foundation after construction, when the empty dam is then filled with water. The calculation of the settlements will help us to estimate the value of the boom (extra height) to be added with respect to the actual height of the crest of the dam, the aim being that with time the boom will compensate for the post-construction settlement thereby maintaining the freeboard

Keywords

settlement, embankment, backfill, foundation, boom.

Introduction

Lom Pangar is situated at the confluence of the Lom and Pangar Rivers in the Eastern Region of Cameroon about 420 km east of capital city Yaoundé. The development objective of the Lom Pangar Hydropower Project for Cameroon is to increase hydropower generation capacity and reduce seasonal variability of water flow in the Sanaga River and to increase access to electricity. [8]

Any structures constructed on a compressible soil layer will eventually consolidate and settle at the level of the foundation. So too, embankments made from backfill generally do consolidate due to the backfill load and have a post-construction settlement of the foundation. Firstly, the void occupied by air and water will be squeezed out and later some deformation of the particles occur leading to settlement [4], [6], [7]. The assumption here is that this one dimensional (vertical) settlement at the end of construction phase is considered equal to zero [5].

Physical phenomenon at stake

Consider an embankment composed of compacted backfill, impermeable or permeable, placed on alluvial foundation. A particle of the backfill or foundation located below the crest of the dam will support in the course of the history of the dam the following different conditions:

- At the end of construction, the materials will support a vertical load due to the weight of the backfill above the point in consideration. This load is partially counterbalanced by the appearance of interstitial pressures due to the fact that the less impermeable materials cannot expulse quickly and sufficiently the water they contain. Therefore, if the effective vertical stress is almost equal to the weight of the underlying soil, the increase of the effective stress does not vary linearly with the height of the backfill.

- With time, if the dam remains dry for a very long period, the interstitial pressures at the end of construction tend to dissipate, whereas the vertical load practically, does not vary anymore: this is the phenomenon of consolidation [2]. Hence, the vertical stresses have a tendency to increase with time. This increment in effective stress has a tendency to increase the vertical deformation of materials and consequently a settlement of the dam in the long run.

- If the dam is rapidly filled with water, a flow network will be established in the body of the backfill and the foundation and the pressure at the end of construction will be dissipated only partially thus causing lesser settlements than the previously discussed case. The difference between the two situations is compensated by the fact that when the dam is filled with water, the materials upstream will saturate and have a tendency to crumble brutally: this is the phenomenon of crumbling by saturation [1].

In our case what concerns us is the third situation. The increment in settlement between the short term (just after construction) and the long run corresponds to the rebound height to be given to the backfill. The long term settlement is calculated by putting ourselves in the second case: dam never filled with water corresponding to complete consolidation, keeping in mind that by this method, the settlement will be overvalued.

Calculation of settlements

To calculate the settlement of the dam and its embankment and its foundation, we advance the following hypothesis:

- The dam and its foundation can each be labelled as infinite layer of material: the state of deformation and the stress of an element of the backfill and the foundation correspond therefore to oedometric conditions.

- It follows that the vertical load (in total stress) is at all instant equal to the weight γh of the backfill above (with γ the volume weight and h the height). In the short term, just after construction, the weight is only partially transmitted to the skeleton of the material, the other part being held up by water trapped within the grains. The interstitial pressure which has developed within the material at a height h below the backfill is equal to Ru x γh, Ru being the coefficient of interstitial pressure of the material. The increment of the effective force is thus equal to (1-Ru) x γh. In the long run, the interstitial pressures are dissipated entirely and the increment in the effective stress is equal to γh.

- The vertical deformation of the εz of materials of the dam or of its foundation is directly dependent on the effective stresses.

When the effective stress increases from σ_ν0 to σ_νthe deformation variation is given by the following relation:

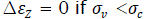         eq1

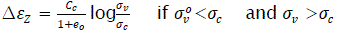     eq2

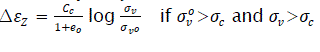    eq3

With e₀being the initial void ratio and the parameters σ_c and C_cbeing respectively the consolidation stress and the coefficient of consolidation measured from the oedometer. The settlement caused by a load inferior to the consolidation stress is assumed equal to zero.

Settling of the foundation

An element of the foundation situated at a height H under natural ground is submitted to an initial stress:

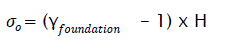      eq4

With γ _foundation = saturated density of the materials of the foundation

At the end of construction when the height h of the backfill has been put in place, the effective stress is:

         eq5

With γ_backfill the density of the backfill put in place and RU_foundationthe coefficient of interstitial pressure of the foundation materials. That is:

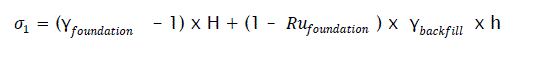    eq6

We conclude with the following relations:

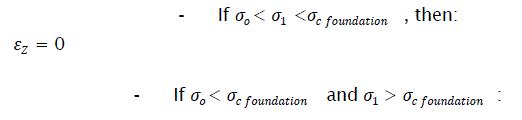      eq7

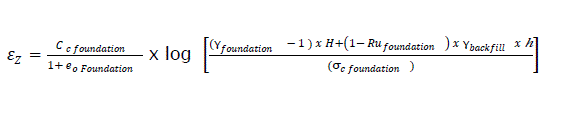     eq8

      eq9

These settlements are not part of the efforts to obtain the extra height because the height we are talking of in this article is the settlement as from the end of construction. In practice the settlement that occurs during construction is compensated for by putting extra materials.

In the long run, the effective stress on an element in the foundation is:

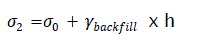      eq10

Since we suppose that the dissipation of the interstitial pressures is total (total consolidation) the settlement produced just after the end of the construction and in the long run is calculated as follows:

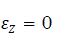     If σ₀< σ₂< σ_{c foundation ,} then      - If σ₀< σ_{c foundation ,}and σ₂< σ_{c foundation}      eq11

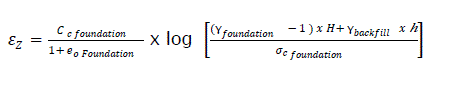      eq12

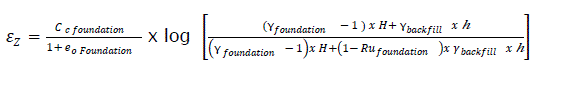    eq13

The value of ε_Z calculated here gives the settlement of the foundation to be taken into account when calculating the boom of the embankment.

Settlement of the dam (embankment)

At the time of putting in place (corresponding to the initial state of the materials) a backfill element is under an initial stress equal to zero.

At the end of construction, when a backfill of height h has been put in place above the element considered, the effective stress is:

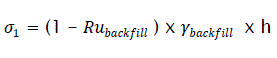     eq14

with Ru being the coefficient of interstitial pressure of the backfill material.

The settlement produced between the initial state (at the start) of construction and the end of construction is calculated as follows:

 

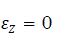   If σ₁<σ_{c foundation ,} (consolidation stress of backfill) then:

                      - If σ₁>σ_{c foundation} then:         eq15

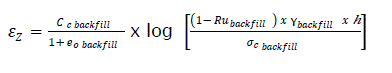      eq16

As in the case of the foundation, the settlement ε_z calculated here is the settlement at the end of construction and is not taken into account when calculating the boom to be added to the embankment.

In the long run, the effective stress felt by an element of the backfill situated at a distance h from the crest is:

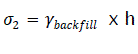      eq17

We suppose that the dissipation of interstitial forces of the embankment is total.

The settlement produced from the end of construction onward is:

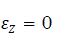 If σ₁< σ₂< σ_{c backfill}, then:   - If σ₁< σ_{c backfill}and σ₂< σ_{c backfill}, , then:        eq18

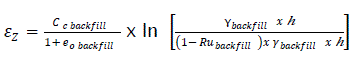      eq19

          - If σ_{c backfill},< σ₁< σ₂

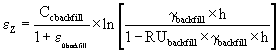
The value of ε_z calculated here is to be added to that from foundation to obtain the extra height to be added for a backfill of a particular height h.

Characteristic of materials

The analysis of the different settlements of the Lom Pangar dam was obtained by varying the different heights of the backfills and their underlying foundations. The characteristics of the foundations were obtained from recognition and identification tests carried out on both banks of the river. The properties of the backfill materials were obtained following a recognition mission and proctor tests done in laboratories via samples of materials taken from the area for which backfill materials were to be obtained [3]. The properties obtained are reported in the following table:

Results

The results for settlement of embankment in the long run and calculation of settlements in both the foundation and the backfills are shown below:

Conclusion

We have to recall first of all that the backfill works covering both banks are composed of:

- An embankment of mixed materials (partly earth fill and partly rocks) having a clayey core place all over on rocky bed estimated at an altitude of 632 Cameroon geographic level (CGL).

-An embankment of backfill laterite soil placed on natural soil. Its height varies in with respect to from the riverbed as well as the thickness of the foundation.

The settlement, in the long run, is presented with respect to the height of the backfill as shown in table 2 and figure 1. The results take into account the fact that the depth of the compressible foundation is variable. At each stage of the calculation the sum of the height of the backfill and the depth of the foundation is equal to 45.55m (which is equal to the distance between the height of the crest of the dam and the bedrock surface).

In the case of the case of the embankment made of backfill laterite soil, the settlement has been decomposed into two parts, namely:

- The actual settlement of the clayey foundation

- The settlement of the backfill itself

In the case of the embankment made of mixed materials, extra height to be put in place is 1.1m. In the case of the embankment made of backfill laterite soil, the highest settlement in the foundation is 83cm and that of the backfill is 81cm. In all, the joint settlement of the foundation and the backfill is a maximum of 1.29m, which is 2.8% of the total height. The thickness of the foundation and the height of the backfill do not vary in the same direction, as the maximum settlement of the foundation is not attained when the height of the backfill is maximal but when it is intermediate (that is around 20m).

References

1. Aberg A. Void ratio of non-cohesive soils and similar materials. J Geotech Eng. 1990;118(9):1315-1334.
2. Augustesen A, Liingaard M, and Lade PV. Evaluation of Time-Dependent Behavior of Soils. Int J Geomech. 2004;4:137-156.
3. COYNE et BELIER. 2009, Avant-ProjetDétaillé du Barrage de LomPangar Doc. n°10108-NDC-0600-B Etude de la Stabilité du Barrage BCR.
4. Dascal O. Post-construction deformations of rockfill dams. A S C E J GeotEngng. 1987;I 13(1):46-59.
5. Day Robert W. Foundation Engineering Handbook, 2006, pp7.34-7.40, McGraw-Hill, New York, NY.
6. Duplanic N. 1989, Landfill deformation monitoring and stability analysis. Conf. Geotechnics of Waste Fills - Theory and Practice. Pittsburgh PA. USA.
7. Thorson, B. 2001, “Surcharging? How Much? How Long?” Proceedings of the 49th Annual Geotechnical Engineering Conference, pp. 1-14.
8. www.worldbank.org/projects/P114077/cm-lom-pangar-hydropower-proj-fy12?lang=en