International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

DIAGNOSIS APPROACH USINGBOND GRAPH AND TIMED AUTOMATA

H.Dhouibi1, M.Bochra2, Z. Simeu Abasi3, M. Hassani4
  1. Assistant professor, LARATSI, National Engineering school of Monastir , Tunisia
  2. PhD Student, LARATSI, National Engineering school of Monastir , Tunisia
  3. Professor, G-SCOP, Grenoble- IPN/UJF- Grenoble 1,CNRS , France
  4. Professor, LARATSI, National Engineering school of Monastir , Tunisia
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Modelling and analysing dynamic system behaviour is the key to successful the step in Fault Detection and Isolation(FDI)of industrial process. The problem of fault diagnosis involves detecting, locating and identifying the consideredfaults occurring in the dynamical system. The aim of this paper is to explain the use of hybrid tool which combines Bond Graph (BG) and Timed Automata (TA). These tools allow us, respectively, to detect the fault and find the cause of a system dysfunction. Due to structural and causal properties of the bond graph tool, we use it for detecting the incorrect behavior. For the phase of fault location and fault identification we use the timed model (timed automata). The proposed approach is validated through simulation tests to a level regulation system.

Keywords
Diagnosis, Bond Gaph, Timed Automata, Analytic Redundancy Relations.

INTRODUCTION
Supervision is a set of tools and methods used to operatea process in normal situation as well as in the presence offailures. There is an abundance of literature on process fault diagnosis ranging from two different communities: the SystemsDynamics and Control Engineering (FDI) community[1,2] and the Artificial Intelligence Diagnosis(DX) community [3,4]. The two communities haveemployed different kinds of models, and made differentassumptions concerning robustness of the generatedsolution with regard to modeling errors, measurementnoise, and disturbances. They are quantitative model-based methods, qualitative model-based methods, and process history based-methods.The general principle of allmodel-based FDI approaches is to compare the expectedbehavior of the system, given by model, with its actualbehavior. The first step of a FDI procedure consists ingenerating a set of residuals. These residuals are specialsignals that reflect the discrepancy between the twobehaviors. Analytic Redundancy Relation (ARR) methodsare classically used for residual generation in the FDIcommunity [5]. The DX community has developedmethods such as possible conflicts [6, 7], and analysis oftemporal causal graphs [8, 9] for diagnosis of continuoussystems. These methods are based on the structuralanalysis of dynamic models, much like the ARR schemesdeveloped by the FDI community. The two communitiesuse different algorithms, but the overall framework forfault isolation is similar, defined by a two-step process: residual generation, followed byresidual evaluation[2, 3].
The main purposes of this paper concern residual generationand fault isolation based on a new approach which combined the causal graphicalapproaches (Bond graph and causal graph) and the timed automata. Thebond graph model is used to generate systematically a setof fault indicators called also analytical redundancy relations(ARRs)deals with the FDIaspect using Bond Graph-based modeling approach.This methodmodeling approachprovides an effective tool for compositionalmodeling and fault detection and isolation (FDI) of dynamic systems [10], [11].ARRs are designed; the fault detectionprocedure checks the presence of fault indicated by a non-zero value of these indicators. We use the timed automata for locate the source of failure. In theapproach we propose here, the diagnosis system is basedon checking the consistency between the time of failureoccurrences and the inputs sequences. It isthus necessary to know thetime trajectories.Our method is based on the backwardexploitation of the dynamic model, where all possiblereverse paths are searched. The reverse path is theconnection of the faulty state to the initial state.
This paper is organized as follows: In the next section,a proposed procedure for FDI is described. Section III andIV give, respectively, an idea about quantitative (BG) and timed automata (TA) approaches using to developing diagnosis approach.In Section V, An academically example is used toillustrate our approach. Finally, a conclusion is presentedwith some perspectives.

PROPOSED DIAGNOSIS APPROACH
The proposed FDI approach combines two tools: the bon graph and timed automata is shown in figure 1, where variables u, Rarerespectively input state and the set ofresidues.
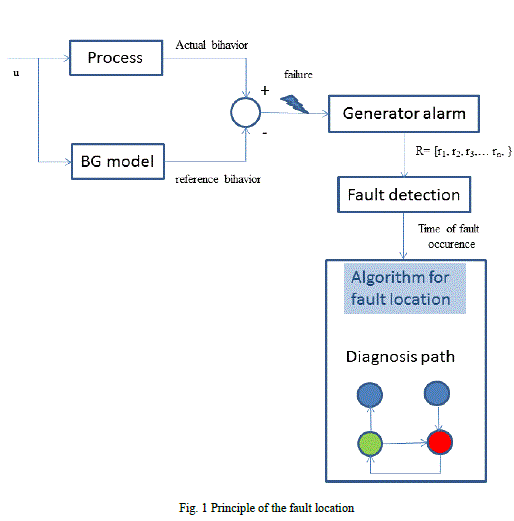image
The quantitative approach is based on the bond graph modelwhich allows the generation of the fault indicators and the dynamic model (AT) which presents a tool of fault location and isolation. The diagnostic technique for fault location is based on time analysis, where the coherent trace is searched by the verification ofelapsed time with global time of alarm.We consider a plant equipped with an alarm andwith a global clock for synchronization. Alarmproduces an error signal when a fault is detected. Ourdiagnosis task is to locate and identify all faults whichcan occur (figure 1). The aim is to find the coherent diagnostic path, which corresponds to the faultyevolution of the system.
In our case verification (analysis) means searching accessible trace of timed automata(reverse path). This reverse path project the evolution of the system, from a final faulty state to the initial state [12]. The reverse path is also called diagnostic path. We suppose the initialstate is known. Our task can be seen as retrace the automaton graph from the faulty statesto the known origin state. The aim is to find from the set of reverse path the coherent ones.

QUANTITATIVE GRAPHICAL APPROACH
A. Bond graph basis
Bond graphs are a domain-independent graphical description of dynamic behaviour of different physicalsystems (mechanical, electrical, hydraulic …). The basis is that bond graphs arebased on energy and energy exchange. BGmodeling is a powerful tool for modeling engineering systems, especially when differentphysical domains are involved.
The concept of bond graphs was originated by [13]. The idea was further developed byKarnopp and Rosenberg [14], such that it could be used inpractice [15][16]. A number of methods have been developed for fault detection and isolation. Allmethods of fault detection work by designing residual functions. The residual represents thedifference between an estimated value and a measured one, which should be zero duringnormal operation, but large in the presence of faults [10].
1) Generalized variables
Thebondgraphbased onthegraphical representation of theenergy exchangeprocesseswithin thesystem to be modelled. These weather applicationscan then beconverted intoblock diagramormathematical formasthestate representation. This modelling approach uses thegeneralizedvariable powerand energy as well asgeneralizedelements: resistor ( R ), compliance ( C ), inertia ( I ), transformer (TF), gyrator (GY), effort source (Se) and flow source (Sf)the intuitiveanalogy voltage- effort. Depending on the physical environment, these variables have different value. Forexample in electrical networks, flow represents the “current” and effort the “voltage”, inmechanical linkages, flow represents the “velocity” and effort the “force”.
On each Bond, one of the variables must be the cause and the other the effect. This can bededuced by the relationship indicated by the arrow direction. Thislinkindicatesthevariablespowerandby conventionthedirection of the half arrowis thedirectioncorresponding to the positivepoweras shown inFigure2. Effort and flow causalitiesalways act in opposite directions in a Bond.
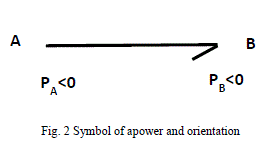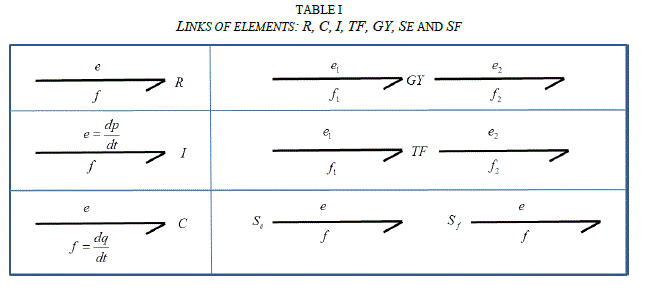
image
The representations of generalized elements, R, C, I, TF, GY, Se and Sf, are shown in Table 1. The elements R, C, I are passive, they receive energy from which the direction of their bond. TF, GY are conservative elements, they only transfer energy where the orientation of links (incoming and outgoing).TF, GY is active elements, it provides energy, and their bond is coming.
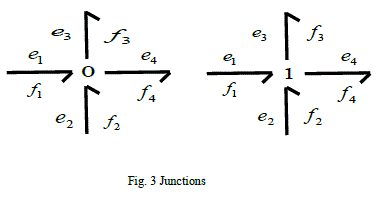
image
1) Junction elements
There are only two kinds of junctions, the 1 and the 0 junction (fig. 3). They conserve power and are reversible. They simply represent system topology and hence the underlying layer of junctions and two-port elements in a complete model (also termed the Junction Structure) is power conserving. 0 junctions have equality of efforts while the flows sum up to zero, if power orientations are taken positive toward the junction. 1junctions have equality of flows and the efforts sum up to zero with the same power orientation.
image
B. Generation of fault indicators
The diagnosis using bond graph models requires the generation of Analytical Redundancy Relations whichrepresentthe set of constraints deduced from the model of the system containing the different known variables(measurements, sources and parameters) [17][18]. ARR are obtained from the behavior model of the system through differentprocedures of elimination of unknown variables.The online evaluation and analysis of these indicators allow to detect and to isolate faults affecting the process.Numeric evaluation of each ARR is called a residual, which is used in model basedFault Detection and Isolation (FDI) algorithms.
The numerical evaluation of an analytical redundancy relation led to a residual of this form:
r = f (K) = f (De,Df ,Se,Sf ,MSe,Sf ,u,θ ) = 0
whereK is the set of known variables and/or parameters. In a bond graph sense,the set of known variables represents the outer vertices (the flow Dfand the effortDe detectors, the flow Sfand the effort Se sources, the modulated flow MSfandeffort MSesources, the process inputs u and the process parameters θ) [21].
A residual is sensitive to faults of the jthcomponent if and only if one (or more)parameter belonging to the jthcomponent appears inri .
A fault indicator algorithm is given as follows:
1) Preferred derivative causality is assigned to storage elements and detectors that becomes dualized;
2) Deduce equations of behavior FB, junctions FJ, measurement Fy, controlled sources FAand of controller system FC;
3) Unknown variables are directly eliminated from the BG model using covering causal path rules;
4) For any detector whose causality is reversed, an ARR is deduced.
C. Fault signature matrix
Once the ARRs are designed, they lead to the formulation of a binary fault signature matrix ji S which informs us on the sensitivity of residual to the components failures of the physical process (sensors, actuators, etc) [17] [18]. The matrixis defined as:
image
The matrix S ji is called fault signature matrix which provides information on the localization and detection of a failure during the system operation. A failure of a component is detectable if the variable associated with the component is presented in at least an ARR, this failure is isolable if its signature is single (unique) i.e. different from the signatures of the other components.
D. Fault Detection Bond Graph model
The main steps of the FDI bond graph based method to generate the ARRs, the residuals and the corresponding fault signature matrix are summarized hereafter. Interested readers can find more details about the method in [23, 22].
• Build the bond graph model in preferred integral causality.
• Put the bond graph model in preferred derivative causality (with sensor causality inversion if necessary).
• Write for each junction its corresponding equations.
• Write the constitutive equation for each bond graph element.
• Eliminate the unknown variables from each junction equation involving a detector (or a sensor) by covering the causal paths on the bond graph model in derivative causality.
• Generate the ARR, the residuals and the corresponding fault signature matrix.

THE TIMED AUTOMATA
The timed automata tool [19] [20] is defined as a finite state machine with a set of continuous variables that are named clock. These variables evolve continuously in each location of the automata, according to an associated evolution function. As long as the system is in one state Li, the clock xi is continuously incremented. Its evolution is described by X=1. The clocks are synchronized and change with the same step.
An invariant is associated to each state. It corresponds to the conditions needed to remain in the state. The number of clocks depends on the parallelism in the system. The automata can stay in one state as long as the invariant condition is checked. Each transition of an automata is conditioned by an event or temporization called “guard” and its execution determines the discrete evolution of the variables according to its associated assignment.
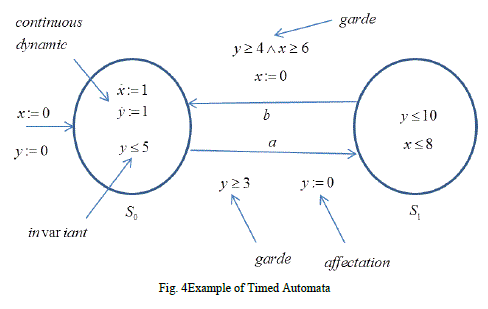
Let us consider the timed automata given in figure 4. This automata has two clocks x and y. The continuous evolution of time in this model is represented by x=1 and the labelled arcs in the graph represent the model of discrete evolution. The guard in each arc is a transition labelling function that assigns firing conditions with the transitions of the automata. The affectation is a function that associates with each transition of the automata one relation that allows actualizing the value of continuous state space variables after the firing of a transition. The invariant in the state S0 and S1 are respectively y ≤ 5 and x ≤ 8. The initial state of this system is represented by an input arc in the origin state (S0). In the dynamic model, active clocks are found in each state. A graphical interpretation of the timed automata is the automata graph (Fig. 4).
image
In our case verification (analysis) means searching accessible trace of timed automata(reverse path). This reverse path project the evolution of the system, from a final faulty stateto the initial state. The reverse path is also called diagnostic path. We suppose the initialstate is known. Our task can be seen as retrace the automaton graph from the faulty statesto the known origin state. The aim is to find from the set of reverse path the coherent ones. 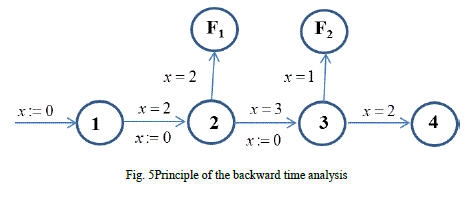The principle of the analysis is shown in automaton graph with faultmodel (Fig.5). From fault model one can see that fault F1 can occurs from states 2,and the fault F2 from the state 3. The diagnostic model must be defined that if fault occursin the system, fault must be located according the time instant. If the fault occurs in thetime 4tu, it’s fault located as F1. In another case, the fault occurs in the time 7tu, the faultF2 is located.
image

APPLICATION EXEMPLE
A. General description of the system
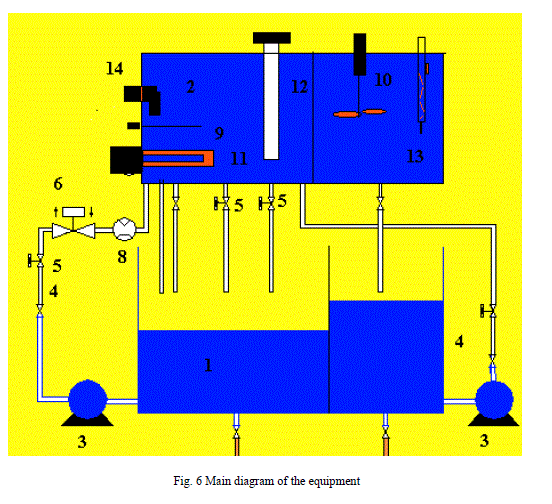
This unit (Fig 6) consists on a hydraulic circuit, with an bottom tank (1) and asuperior process tank (2), both dual ones, two pumps of centrifugal circulation (3),two flowmeters with a manual control valve (4), three on/off solenoid valves (5) anda motorized proportional valve (infinitely variable) (6). Of course, together with thetubes, the union elbows, connections, feedthroungh, main valve and the appropriatedrainage for the circuit operation.
As additional fixed elements, there is also a turbine flow sensor that isinstalled in one of the upward lines of flow (8), and a temperature sensor located in alateral bottom of the process tank (9) together with a serpentine with electric heating(11).
The interchangeable additional elements are an agitator (10), theimmersion level sensor should be located in the process tank (12) and the pH sensor(solenoid), can be in the process tank or also in the second tank (13), to study theeffect of the time out.
image
B. Operation of the subsystems
For the level, flow and temperature control test, the liquid (water) isimpelled from the tank by the pump, located to the left of the front of the equipment,going through the flowmeter, the solenoid valve (usually open), the motorized valve,the turbine (flow sensor) and the process tank. It is possible to use the second pumpin the level tests, as it will be indicated.
The pH control test of requires a second parallel line of flow (right),provided only with pump and a flowmeter. The compartments of the inferior tankshould be loaded with diluted solutions of an acid and a base, respectively. The process tank is divided in two halves, with an orifice between themthat allows their communication or isolation. The right compartment has an overflow of variable level (that it preventsthe complete overflow of the tank, and it allows to modify its effective liquidvolume), two drains with solenoid valves with different Cv (normally closed), and athird one with a normal drainage valve.The left compartment is only connected to a drainage valve. The level control tests require all the elements of the circuit and of thetank, besides the sensor located in it. In some experiments, it is required the secondpump placed to the right-hand side of the equipment.
The Temperature controltests, in these cases, as we will see lateron, can be carried out with experiments in closed circuit or in open circuit. In theclose circuit case, fill the superior tank with the right pump 1 (AB-1) and carry outthe experiment. In open circuit, keeps a constant water flow using the pump 1, thisway, a small water flow is adjusted and the superior overflow is used as a drainagesystem. In this case, it is necessary to use the agitator to guarantee goodtemperature uniformity.
We include in the following table II the elementsconstituting the equipment and a brief description ofeach.
image
E. Fault detection based on bond graph
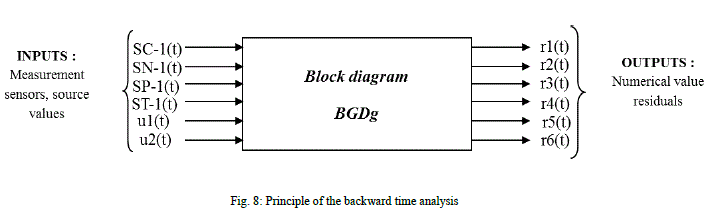
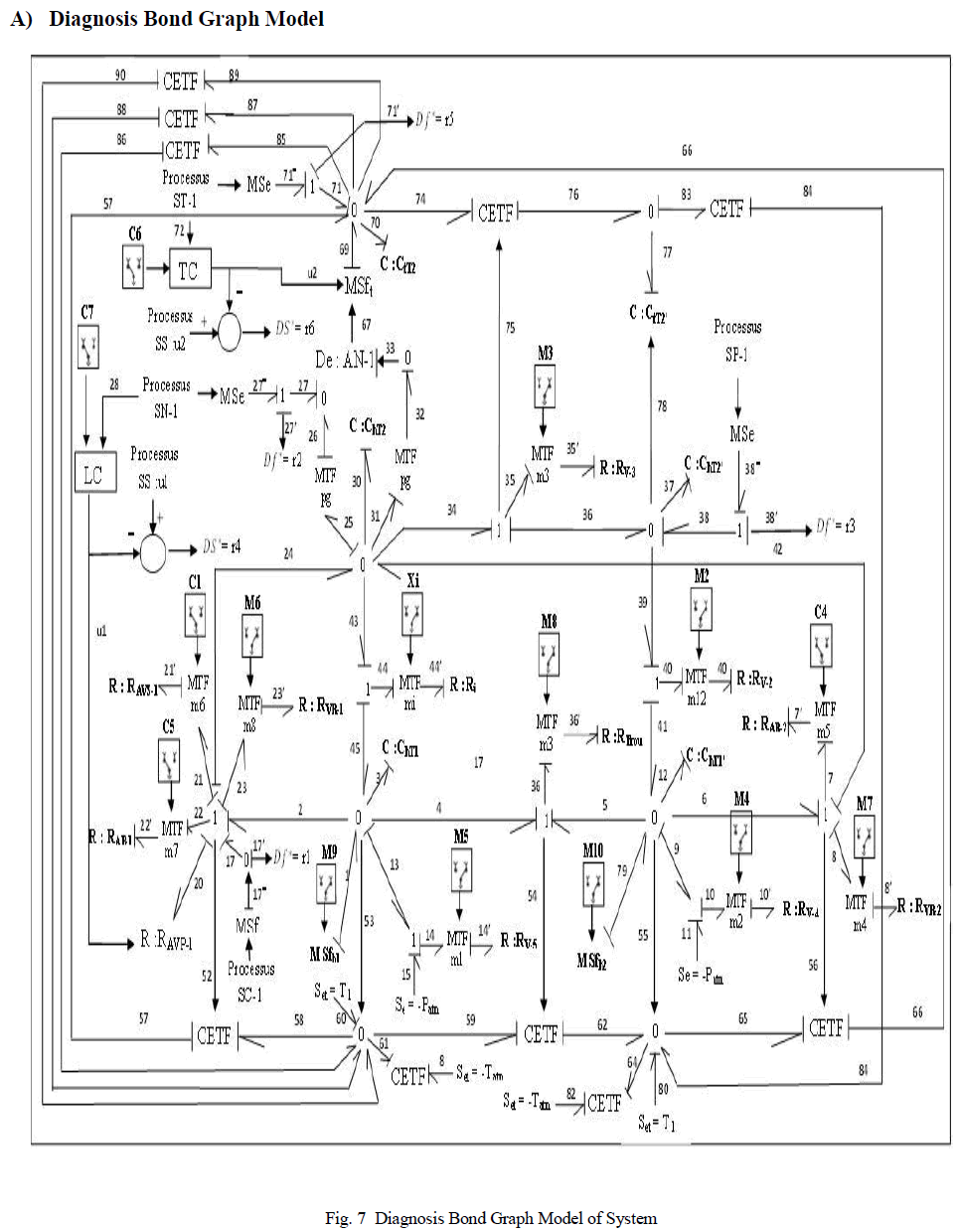
We applied themain steps of the Fault Detection and Isolation bond graph (see §III). The bond graph model diagnosis of the system obtained is given in figure 7 (see Appendix).It has fiveaccess points (corresponding to the five sensorsof the system)and fiveoutputs (corresponding to the five digitalresiduesgenerated) as shown in theblockdiagram in Figure8
image
1) ARRs generation
Methods to derive ARRs from bond graph models by applyingthe causality inversion algorithm have been presentedin [25] [16], which use structural and causal properties.The ARRs are deduced from junctions 1 and 0 that containdetectors on the bond graph model in preferred derivativecausality, Figure 9. The unknown variables are eliminated bycovering causal paths from detectors to unknown variables.This leads in fact to oriented graph.
In our case the diagnosismodelBGprovidesnumerical valuesbut alsotheresiduessignature matrixSijfailures. Indeed,itis essentialfor the localization offailuresthat may occur duringsystem operation.The path of thecausalpathsofthe unknown variableto the detectoris used to constructthesignature matrixfailures (Table III). Thus, aresidualriis sensitive toa failure in thecomponent jif and only ifthe variable associated withthe latteris present in thecausalpath forthe generation ofresiduallaughed.
For example,thecomponents involved inthedetectorresidue r1are determined bythe followingcausalpaths:
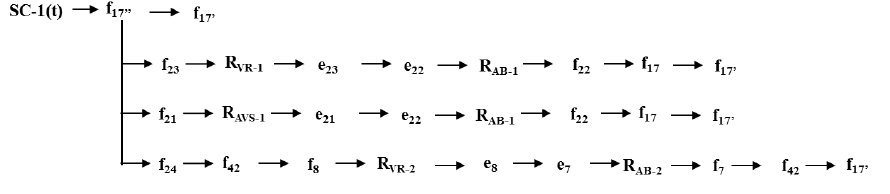image
The components involvedin theresidue r1aregivenby the vectorK1 =[SC-1, RVR-1-1 RAVSRVR-2, RAB-1, RAB-2, SN-1, SC-1 RAVP, tankT1, tank T1'].Thusthe application of thisprocedure on alldigitaldetectorsresiduesled to thefailuresignature matrixSij.Thefault signature matrix of the diagnosis modelis givenin TableIII
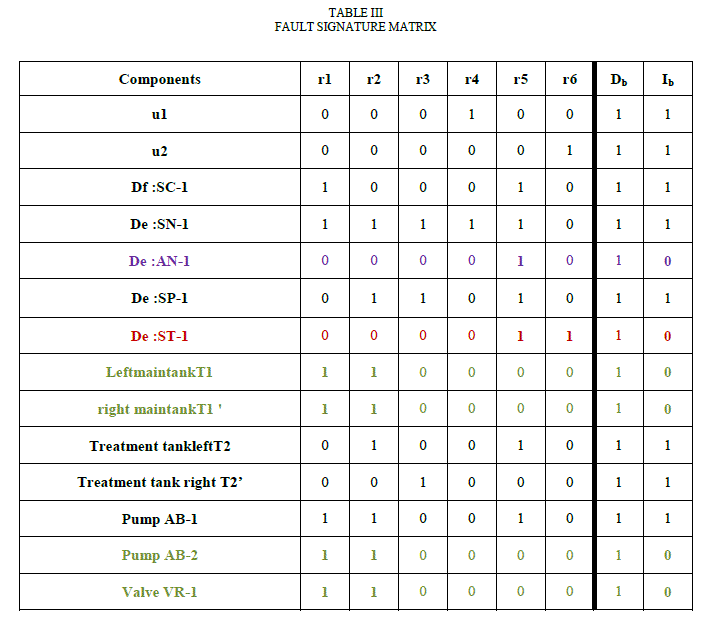image
image
It is importantto note that thesignature matrixfaultsconstructed fromcausalpathscorresponds toa definiteconfiguration(ormode)and thereforethe associatedmodel.Theform of the equationsfor eachelementbondgraphis then the sameduring the whole periodof operation ina given configuration.For example, thetotal blockageof the valveAVS-1 representedby the elementRAVS-1 causes the rupture ofallcausalpaths(andtoward) the item. By analysing this matrix,we see thatthe variable associated witheach component ispresent in atleast one residue. So allsystem failuresare theoreticallydetectable(= 1).
In addition, the signatures of componentsSN-1, SC-1, U1, U2, SP-1, AB-1, V-3, tankT2, tank T2 'and LCare uniquemeaning thatthefailureof these componentsareisolatable(Ib = 1). Forcons, the signatures of theST-1andTCcomponentsare identicalwhich meansthat defectsaffecting thesecomponents cannotbe isolated(Ib= 0).
Our contributionin thispaperis the use oftimed automatafor the isolation ofthese non-isolablecomponentsbyBond Graphmodel.
F. Fault isolation based on timed automata
For thephase oflocalization offaultswe consider onlypart ofthe model shown in Figure9.The goal isthe study ofthe levelin a tankby the actionofthe valveAVP1andalsoby twosensors SN1 and AN1, respectively,measuringhighlevels andlow.
We use thetimedautomatonmodeltoisolate faults insensorswhicharenotidentifiable(see TableIII).
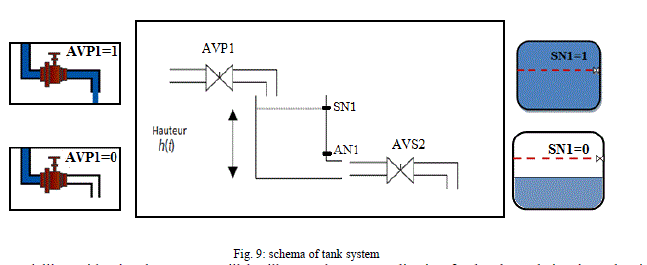image
Example: modelling with Timed automata will be illustrated on an application for level regulation in tank wich is equipped by two level sensors and two valves. Valve AVP1as input valve, output valve AVS2.Figure 9, shows the placement of two levels sensors.
Control: Firstly,the valve AVP1 is open; the liquidflows into tank 1.When the tank level AN1 is reached, the valve AVS2 is is opened. Then, When the tank level SN1, the valve AVP1 is closed..
Control sequence:
(1) S0: When the process is initialized, tank shouldbe empty.
(2) S1: First, valve V1 is open, a liquid flows into tank.
(3) S2: If level AN1 is reached then valve AVS2 is opened.
(4) S3: If Level SN1 is reached then AVP1 is closed.
The aim of backward time analysis of timed automata isto locate (isolate) a fault. In our case exploitation meanssearching accessible trace according the time from a finalfaulty state to the initial state of automaton denoted byreverse path. Therefore the initial state must be known.Our task can be seen as retrace the automaton graph fromthe faulty states to the known origin state. The aim is tofind from the set of reverse path the coherent ones. 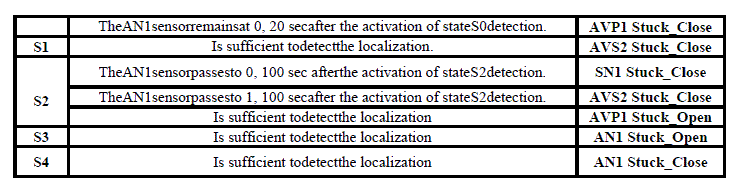In our case whichwe considereight faultsas well as their failure modes aresummarized in Table IV.
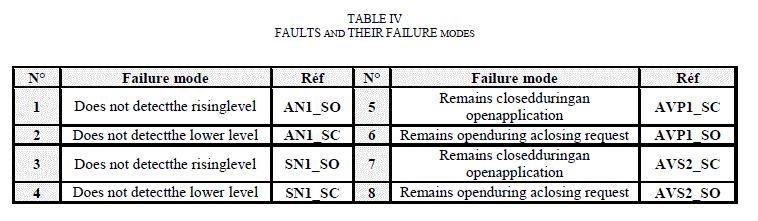image
For these eight faultslisted, it uses onlyfivestatesdetection(S0, S1, ...,S4).Thetable V belowshowsthe conditions necessaryto locationfault.
image
image
This algorithmbased on thetime of occurrenceof the alarm,to localizethe fault.
Step 1: Calculate theduration of a cycleof operation is (in our case it is 418.9sec).
Step2: first calculate the numberof cycles performedby the processbefore the activationof the alarm. Number of cycles= round(talarm/418.9)
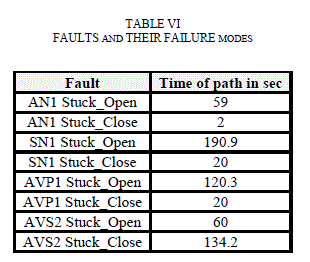
Step 3: Thenthe weight of thepathis calculated: Talarm-path =(418.9 *(number of cycle))
Step4:comparethe value obtained withtheweight ofdifferent ways
In the tablebeloware listedthe weights ofdifferent paths.
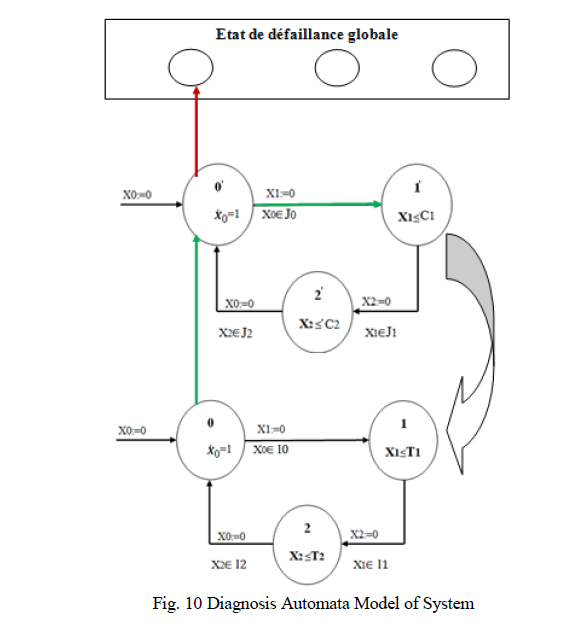
image
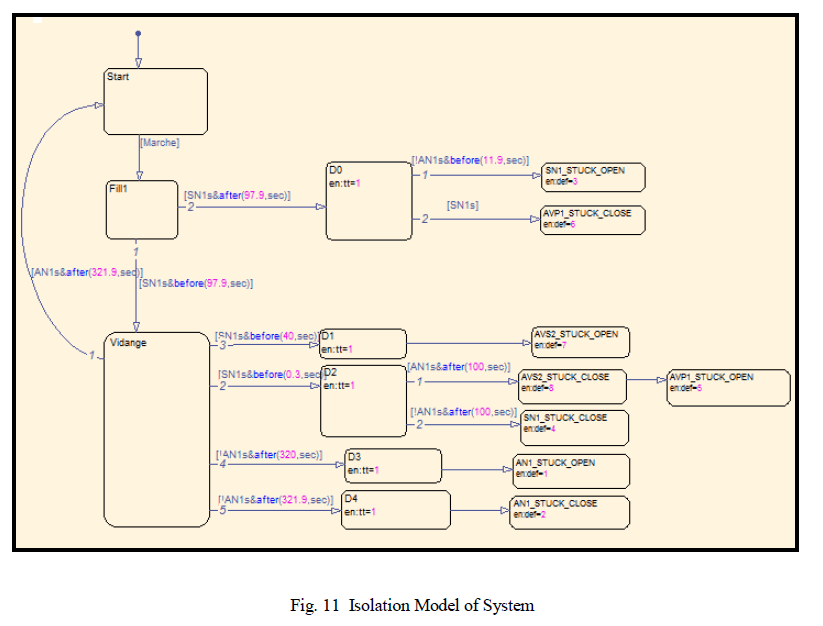
The global automata graph for diagnosis of the two tanks system is shown in figure 10 (see Appendix B).If the modelof the whole systemis built, the reading of theevolution of the systembecomes very difficult.Usingthe tooltimedautomatonhasonly one drawbackis the explosionin the number oftransitions betweenstates inthe threemodes.Thisexplosion probleminthe number of arcsis solved byusing thetoolstate flow (see Figure 11 in Appendix C)

SIMULATION RESULTS
To illustrate the effectiveness of the diagnosis approach, wepresent simulation results of the level regulation system example.
The Bon graph and timed automata models of the system was constructed using MATLABSIMULINK and state flow. Bond graph block and bloc program are developed by the authors which are not presentedin the paper
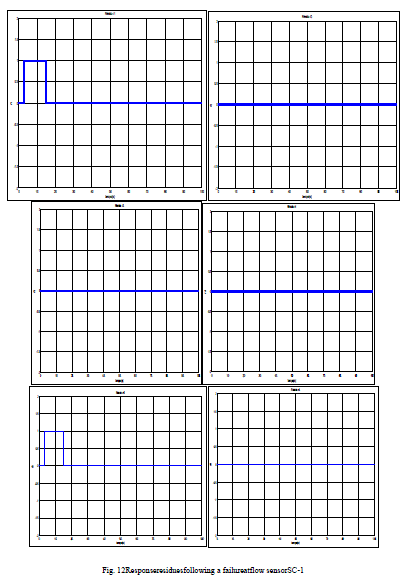
Two failure scenarios were simulated. The first failure SC-flow sensor 1 during a time interval ranging from 3 to 15 s. Figure 12 shows the response of r1 and r5 residues and their sensitivity to this failure. Referring to the signature component SC-1 (flow sensor) given in Table III shows that this result is consistent with what is planned, ie in case of component failure SC-1 (flow sensor) only the residues r1 and r5 exceed their respective thresholds.
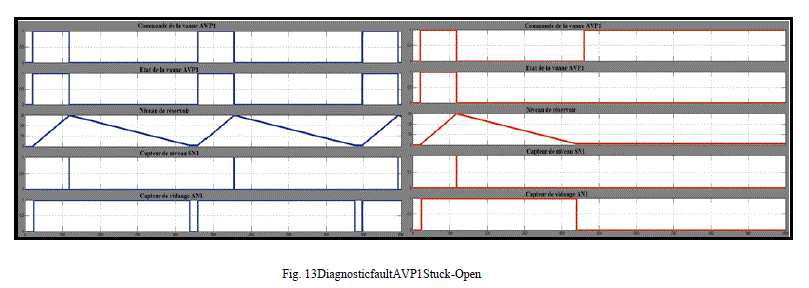image
image
Figure 13 enables us to comparenormal operation (left) of the process witha state offailedoperation(right). Onthe right figure, despite the application to opentheAVP1valveremains closed. This time represents theoccurrence of a failure. Toccurence=601.9sec.
Then,thesensorSN1,remains in stateS0,97.9secafterthe request to opentheAVP1valve.This momentisthe moment offault detection. Tdétection=699.8sec. S0state.
FinallyAN1sensorremainsat 0, 20 seconds afteractivation of thedetection state. This momentcorresponds to thefault location. Tlocalisation=719.8sec.
Thisfigure analysisshows that:
• Detection time=Tdétection-Toccurence=97.9sec.
• Localization time=Tlocalization–Tdétection=20 sec

CONCLUSION
In this paper, a method for fault detection and isolation ispresented. It is combining graphical approaches (BG) and the model of dynamical system (timedautomata). Bond graph is used for detecting systematically actuators; sensor and structural fault.Also the fault isolation procedure based backward timeanalysis was presented. The localization algorithm is used when the faults can not identify from the model of Bond Graph.
This isolation approach is based on trajectory and temporaltransition of the model must be identified for allconsidered modes (faultless and faulty modes). Thetime of occurrence of fault is considered. The backward time analysis searches the possible reversepath to localize the fault according the time of faultoccurrence. Thenext stepis interestedin the eventoffault diagnosisin the presence ofcommon causes.

ACKNOWLEDGMENT
The authors would like to thank the editor and refereesfor their insightful comments that greatly improved thecontent of this paper.

References























Appendix
image
B) Diagnosis Timed Automata Model
image
C) Isolation Model constructed with state flow
image