International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Dijkstra’s Shortest Path Algorithm for Road Network

K.Rohila1, P.Gouthami1, Priya MM2
  1. MS(SE), School of Information Technology and Engineering, VIT University,Vellore, Tamil Nadu, India
  2. Assistant Professor (Senior), School of Information Technology and Engineering, VIT University, Vellore, Tamil Nadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Shortest Path problems are inevitable in road network applications such as city emergency handling and drive guiding system. Basic concepts of network analysis in connection with traffic issues are explored. The traffic condition among a city changes from time to time and there are usually huge amounts of requests occur, it needs to find the solution quickly. The above problems can be rectified through shortest paths by using the Dijkstra’s Algorithm. The main objective is the low cost of the implementation. The shortest path problem is to find a path between two vertices (nodes) on a given graph, such that the sum of the weights on its constituent edges is minimized. This problem has been intensively investigated over years, due to its extensive applications in graph theory, artificial intelligence, computer network and the design of transportation systems. The classic Dijkstra’s algorithm was designed to solve the singlesource shortest path problem for a static graph. It works starting from the source node and calculating the shortest path on the whole network. Noting that an upper bound of the distance between two nodes can be evaluated in advance on the given transportation network. In order to solve the problem, we have been implemented shortest path for road network by using Applets in a programing language java. Software required for this application is jdk1.7.0_01.

Keywords
shortest path; Dijkstra’s Algorithm; Breadth First Search; maximum number of nodes;

INTRODUCTION
This paper involved in illustrating the best way to travel between two points and in doing so, the shortest path algorithm was created. Dijkstra‘s Algorithm is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree. This algorithm is often used in routing and other network related protocols. For a given source vertex (node) in the graph, the algorithm finds the Sfinding costs of shortest paths from a single vertex to a single destination vertex by stopping the algorithm once the shortest path to the destination vertex has been determined. For example, if the vertices of the graph represent cities and edge path costs represent driving distances between pairs of cities connected by a direct road, Dijkstra's algorithm can be used to find the shortest route between one city and all other cities.
A large amount of work has been done on finding shortest paths through abstract. Dijkstra‘s algorithm is a Shortest Path Finding Algorithm which is applicable on a Graph which is Directed and got the Edges weighted with non-negative weights. If we have an undirected graph with edges unweighted, we can solve the problem with the implementation of Breadth First Search (BFS) algorithm. As we know we are unableto use BFS algorithm in case of a weighted and directed graph, but we can modify our algorithm of BFS in such a way that we can handle the above stated issues (weights and direction). We will later know thatDijkstra‘s algorithm is asymptotically the fastest known single-source shortest-path algorithm for arbitrary directed graphs with unbounded nonnegative weights. These are the motivations‘that will help us to know further about the Dijkstra‘s algorithm.

RELATED WORK
The indoor navigational assistance for this type of users [1] presents additional challenges not faced by conventional guidance systems, due to the personal nature of the interactions. The algorithms are part of an overall Indoor Navigation Model that is used to provide assistance and guidance in unfamiliar indoor environments. Path planning uses the Dijkstra's shortestpathalgorithms, to operate on an "Intelligent Map", that is based on a new data structure termed "cactus tree" which is predicated on the relationships between the different objects that represent an indoor environment. This research explores the potential to design an application for the visually impaired even when to- date 'positioning and tracking' system cannot offer reliable position information that highly required by this type of application.The best-path problem for public transportation systems[3], we found that the nature of transfer is that it requires extra costs from an edge to its adjacent edge. So,we use the direct/indirect adjacent edges weighted directed graph as a public transportation data model and improve the storage of an adjacency matrix. We introduce the space storage structure in order to store the scattered information of transfer in indirect adjacent edges lists. Thus, we solve the problem of complex network graphs' storage and design a new shortest path algorithm to solve transit problem based on the data model.Algorithm analysis exhibits that the data model and the algorithm we propose are prior to a simple graph based on the Dijkstra's algorithm in terms of time and space.Today, the increased traffic and complex modern roadnetwork have made finding a good route[4] from one location to another a non-trivial task. Many search algorithms have been proposed to solve the problem, and the most well-known being Dijkstra's algorithm, Johnson's algorithm. While these algorithms are effective for path finding, they are wasteful in terms of computation. In this paper, we present a study to examine both uninformed search and heuristic search based on some major cities and towns.Efficient usage of routing algorithms [16] can significantly reduce travelling distance and transportation costs as well. Usage of the shortest-path algorithm in this case Dijkstra's algorithm for inner transportation optimization in warehouses. The model integrates data such as: 2D graph of warehouse layout, its 3D extension, historical data, ABC analysis and business process model. The prototype of proposed application is tested with sample data and by simulating different working conditions.

DIJKSTRA’S ALGORITHM
Let the node at which we are starting be called the initial node. Dijkstra's algorithm will assign some initialdistance values and will try to improve them step by step. For the first iteration, the current intersection will be the starting point and the distance to it will be zero. For subsequent iterations (after the first), the current intersection will be the closest unvisited intersection to the starting point—this will be easy to find.
From the current intersection, update the distance to every unvisited intersection that is directly connected to it. This is done by determining the sum of the distance between an unvisited intersection and the value of the current intersection and relabeling the unvisited intersection with this value if it is less than its current value. In effect, the intersection is relabelled if the path to it through the current intersection is shorter than the previously known paths. To facilitate shortest path identification, in pencil, mark the road with an arrow pointing to the relabelled intersection if you label/relabel it, and erase all others pointing to it. After you have updated the distances to each neighbouring intersection, mark the current intersection as visited and select theunvisited intersection with lowest distance (from the starting point) – or the lowest label—as the current intersection. Nodes marked as visited are labelled with the shortest path from the starting point to it and will not be revisited or returned to.
image

EXPERIMENTAL RESULTS
In this section, we conduct an experiment to compare the paths between the nodes. In that paths, the shortest path was done by using dijkstra‘s algorithm. Here the shortest path it means low cost was found by the shortest path algorithm. Here java code uses the applets so that applet viewer shows how the shortest path was done. With the use of java software the result was shown in the report. We have got successful result. The experiment was successfully complete. The result of this project finding the shortest path for a single source to to all pairs of vertices by using the Dijkstra’s Algorithm. It gives the cheapest cost and its implementation is easy.
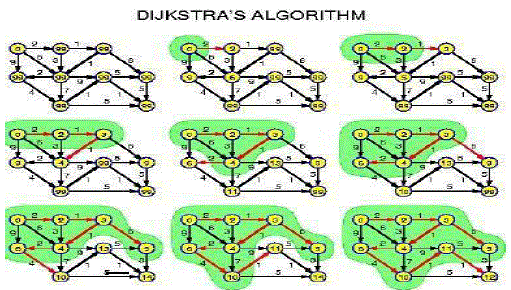
A. Initial:
Algorithm running: Red arrows point to nodes reachable from the start node.
The distance to: b=55, d=50, f=100. Node d has the minimum distance. There is no other arrows coming in to d. Node d will be colored orange to indicate 50 is the length of the shortest path to d.
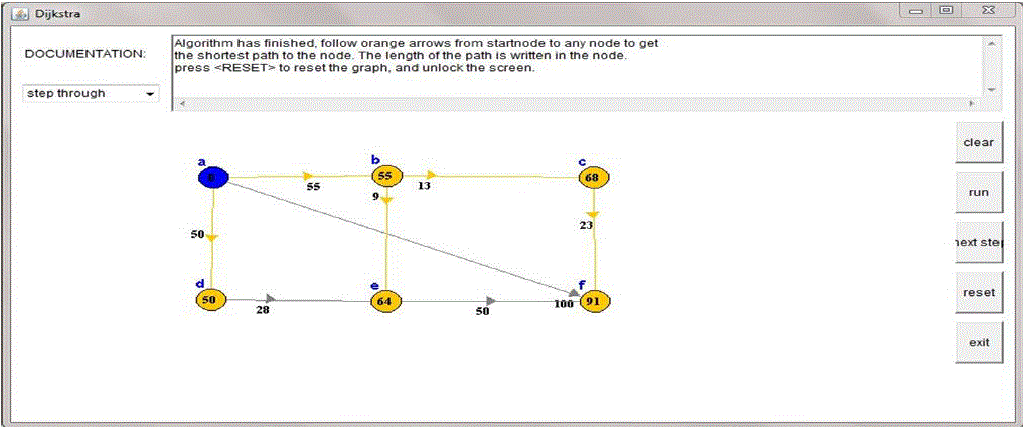
B. Final :
Orange arrows point to nodes reachable from nodes that already have a final distance. The distance to: c=68. There are no other arrows coming in to c.
Node c will be colored orange to indicate 68 is the length of the shortest path to c.Algorithm has finished, follow orange arrows from start node to any node to get the shortest path to the node.

CONCLUSION
We have proposed a practical algorithm for the shortest path problem in transportation networks. The proposed algorithm can limit the search in a sub-graph based on the given nodes of the distance between the two nodes. As a result, the calculation for the shortest path has been simplified. Experimental results on a real-world road network reflect the potential characteristic of the proposed algorithm in comparison to the existing works.
Applets can prove to be very helpful to all the students, in general. Every student who wishes to learn one of the algorithms, implemented in this tool, may use the proposed applet from any remote place, probably his home. It doesn’t matter what his system is. It only requires that the Java Virtual Machine, (JVM), is installed into his system. It should be pointed out that JVM is freely available for download from Sun Microsystems. Moreover there is an intention to enhance the graph editor, in order that the user would be able to draw undirected graphs, or networks, as well. Yet this applet could be further enriched, and possibly visualize more algorithms for digraphs. Directed networks such as the Primal Simplex Algorithm which solves the Minimum Cost Network Flow Problem (MCNFP). Besides more algorithms will be added for undirected graphs such as the Kruskal’s and Prim’s algorithms which solve the Minimum Spanning Tree (MST) problem.

FUTURE WORK
In future release the applet will be modified, in order to be executed as standalone Java application as well. In addition, certain questionnaires will be given to the students of our department to be filled in, in order to get feedback. This is very important, to improve and evaluate the teaching effectiveness of our applet in real instruction environment. Students will also be encouraged to construct their own applets.
 

Figures at a glance
Figure 1 Figure 2
Figure 1 Figure 2
 

References