ISSN: 2320-0189
ISSN: 2320-0189
Joseph KE Ortega*
Bioengineering Laboratory, Department of Mechanical Engineering, University of Colorado Denver, 1200 Larimer Street, NC-3024-F, P.O. Box 173364, Denver, CO, 80217-3364, USA
Received date: 02/06/2016 Accepted date: 17/08/2016 Published date: 23/08/2016
Visit for more related articles at Research & Reviews: Journal of Botanical Sciences
Expansive growth is central to development, morphogenesis, and sensory responses of algal, fungal and plant cells. These walled cells generate turgor pressure by absorbing water. The turgor pressure produces irreversible (plastic) and reversible (elastic) deformations in a wall whose mechanical properties are regulated biochemically. These biophysical processes (water uptake and wall deformation) are described by established interrelated biophysical equations, the augmented growth equations. Dimensional analysis is used to make the Augmented Growth Equations dimensionless, producing dimensionless coefficients. The dimensionless coefficients are interpreted as ratios of biophysical processes. The utility of the dimensionless augmented growth equations and the dimensionless coefficients are explored. It is found that one dimensionless coefficient may provide insight into the wall chemistry used by different cells to regulate their wall mechanical properties. Different magnitudes of the dimensionless coefficient for algal, fungal, and plant cells suggests that different molecular mechanisms are used to regulate their wall mechanical properties.
Morphogenesis, Fungal cells, Glycoproteins, Plant cells, Expansive growth
Volumetric (expansive) growth is fundamental to development, morphogenesis, and sensory responses of plant, algal and fungal cells. These cells can grow to large volumes, e.g. fungal cells (sporangiophores) can grow to lengths greater than 20 cm (Figure 1). These cells are encased in a strong and somewhat rigid cell wall. The cell wall is an exoskeleton that gives the cell shape and support while providing both physical and chemical protection from the external environment. Typical plant and algal cell walls are composed of cellulose microfibrils embedded in an amorphous matrix of hemicelluloses, pectins, and small amounts of structural proteins [1]. Typical fungal cell walls are composed of chitin and β-glucan microfibrils embedded in an amorphous matrix of chitosan, glycoproteins, and lipids [2,3]. The polymers in the walls are linked together by covalent bonds, hydrogen bonds, hydrophobic interaction, and ionic associations [3].
The stage I sporangiophore appears as a single pointed cell that grows longitudinally and vertically at the apical tip in the growth zone. In the scheme on the left, the growth zone is shown as light green and the non-growing stalk is dark green. Clockwise rotation growth (when viewed from above) and elongation growth occur concurrently during stage I producing left-handed helical growth. Stage II begins with spherical growth at the apical tip without elongation and rotation growth. The diameter of the sporangium continues to increase until stage III, where the diameter is constant (≈0.5 mm) and no expansive growth is observed. Stage IVa begins with elongation growth concurrent with counter-clockwise rotation growth (right-handed helical growth) in a short growth zone located approximately 0.6 mm below the sporangium. The sporangium begins to darken and elongation growth, rotation growth, and growth zone length continue to increase. The right-handed helical growth continues for approximately one hour before the rotation rate gradually decreases to zero and clockwise rotation begins without interruption of elongation growth. Stage IVb begins with the initiation of left-handed helical growth and exhibits nearly constant elongation and rotation growth rates for many hours. Stage IVc is initiated by counter-clockwise rotation and right-handed helical growth. Typically, this is a very old sporangiophore. Stage V is the last stage and does not exhibit expansive growth. Reproduced from [4] with permission.
Cells with walls accumulate active solutes inside their semi-permeable plasma membrane. This generates the osmotic potential needed to absorb water from its external environment and produce turgor pressure that stresses the wall. Wall stresses produce irreversible (plastic) and reversible (elastic) wall deformations in three orthogonal directions, generally stretching the wall in the two directions parallel to the wall surface (longitudinally and circumferentially) and contracting the wall in the direction perpendicular to the surface, making the wall thinner [4]. New wall materials (polymers, proteins, etc.) are continuously added to the inside surface to maintain a nearly constant wall thickness that varies between 0.1 μm and 1.0 μm, depending on the cell species [5].
Overall, expansive growth occurs as follows [6]. The cell wall is biochemically loosened to produce wall stress relaxation and pressure relaxation that decreases the magnitude of both the wall stresses and turgor pressure. Water uptake increases in response to the decrease in turgor pressure and expands (deforms) the loosened wall. The wall deformation increases the wall surface area (expansion) while decreasing the wall thickness. Concomitantly, new wall polymers and other wall materials are added to the inner surface of the wall to maintain a nearly constant wall thickness. This sequence of events - wall loosening, wall stress relaxation, pressure relaxation, water uptake, increase in turgor pressure, wall expansion, increase in wall stresses, and wall loosening again - is repeated continually during expansive growth.
Cellular expansive growth rate is generally controlled and regulated by manipulating the mechanical properties of the cell wall to produce plastic deformation, and in some cases by changing the turgor pressure [7]. A considerable amount of research has been conducted to understand how the mechanical properties are controlled at the molecular level [5,8-10]. Mathematical models have been constructed in an attempt to supplement a qualitative description of expansive growth with a quantitative description, to assist in the understanding of growth rate regulation, and to guide experimental investigations.
The qualitative concepts and processes involved in expansive growth have been formalized in quantitative biophysical equations, the augmented growth equations [7,11,12]. The global augmented growth equations describe the two simultaneous and interrelated physical processes that are involved with expansive growth (net water uptake and cell wall deformation) using biophysical variables, thus coupling relevant biology with relevant physics. The first equation describes in relative terms, the rate of change in water volume in the cell, vw, as the difference in the volumetric rate of water uptake, L (Δπ − P), and transpiration, vT [12-14].
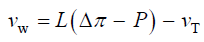 (1)
(1)
Equation 2 describes in relative terms, the rate of change in volume of the cell wall chamber, vcw, as the sum of the volumetric irreversible (plastic) deformation rate, φ (P – PC), and volumetric reversible (elastic) deformation rate, (1/ε) dP/dt, of the cell wall [11].
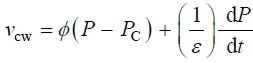 (2)
(2)
During expansive growth the relative rates of change in volume of the water and the cell wall chamber are approximately
equal to each other, and to the relative volumetric growth rate of the cell, 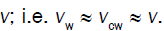 Therefore a third equation can be
obtained by setting (Equations 1 and 2) equal to each other, with the elimination of vw and vcw
[13,14].
Therefore a third equation can be
obtained by setting (Equations 1 and 2) equal to each other, with the elimination of vw and vcw
[13,14].
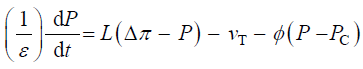 (3)
(3)
The Augmented Growth Equations (Equations 1-3) have accurately described, and in some cases predicted, experimental results from growing plant cells in tissue [7,13,15], algal internode cells [16,17] and fungal sporangiophores [12,18,19]. Reviews discuss many of these experiments and analyses [7,14].
Dimensional Analysis
Additional insight into expansive growth can be obtained by using dimensional analysis. Dimensional analyses is a mathematical tool used in the physical sciences and engineering [20] to obtain insight into relationships between variables involved in processes of interest, to organize large quantities of experimental data, and to provide scaling laws for models. The overall process is to obtain dimensionless groups of variables (Π parameters) involved in the process of interest and explore the relationship between the parameters, experimentally or analytically. A straightforward method to obtain the Π parameters is to make the governing equations dimensionless with constant reference quantities and manipulate the equations to produce dimensionless coefficients, i.e. Π parameters [20]. As an example, the dimensionless linear momentum equation in fluid mechanics produces a dimensionless coefficient for the viscous term that represents the ratio of viscous forces and inertia forces [20]. The inverse of this dimensionless coefficient, or Π parameter, has been termed the Reynolds number (ρ U D /μ, where ρ is the fluid density, U is the flow velocity, D is a characteristic length, and μ is the dynamic viscosity of the fluid). Two Π parameters, the coefficient of drag (CD) and the Reynolds number (ReD), can be used to organize the drag force on a sphere of different diameters (D) produced by hundreds of flows with different fluids and different flow velocities [20]. Analyses of the resultant curve (which represents a functional relationship between the CD and ReD) reveal different flow regions (creep flow, transition flow, laminar boundary layer flow, and turbulent boundary layer flow) that represent different flow patterns and reveals different functional relationships between CD and ReD in these flow regions [20].
The variables in Equations 1-3 are made dimensionless (*) with the following constant reference parameters: vs (steady or average relative volumetric growth rate), vsT (steady or average relative volumetric transpiration rate) and PC (critical turgor pressure); please see analyses, estimates, and definitions for details. Substituting the respective expressions that includes the dimensionless variable and reference parameter for each of the variables into Equations 1-3 and then dividing the first two equations by the constant reference parameter, vs, and dividing the third equation by the constant coefficient, vs PC / ε, we get dimensionless equations with dimensionless variables (*); please see Analyses, Estimates, and Definitions for details.
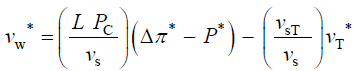 (4)
(4)
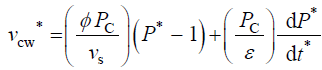 (5)
(5)
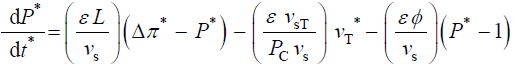 (6)
(6)
Dimensionless Π Parameters
Equations 4-6 are dimensionless and the coefficients for the terms on the RHS (in parenthesis) are also dimensionless. Just as the Reynolds number is interpreted to be the ratio of inertia forces and viscous forces, the dimensionless coefficients in Equations 4-6 may also be interpreted in terms of ratios of processes:

A benefit of using dimensionless equations is that a dimensionless governing equation can be solved and the dimensionless solution can be used to study a wide spectrum of parameter values, without having to solve the governing equation each time [20]. As an example, consider a stress relaxation experiment for some unspecified walled cell. An in vivo stress relaxation experiment is conduct by isolating a growing walled cell from its water supply and eliminating transpiration by testing the cell in an environmental chamber of 100% relative humidity. Then the turgor pressure decays in time and can be measured with a pressure probe [15-18]. Water uptake and water loss from the cell is eliminated so that the decay in turgor pressure is the result of wall stress relaxation alone. Experimentally, the condition that must be satisfied is that the volume of the cell must remain constant during the experiment, i.e. vw = 0 [11,15,18]. The governing equation for a stress relaxation experiment is obtained from Equation 5 by imposing the condition that vcw=vw=0.
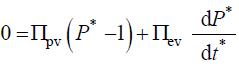
Using the dimensionless initial condition, 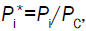 the equation is integrated and the following dimensionless solution
Equation 7 is obtained, where
the equation is integrated and the following dimensionless solution
Equation 7 is obtained, where 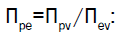
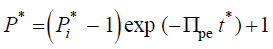 (7)
(7)
It is apparent that the dimensionless time constant, tc*, for the exponential decay of the dimensionless turgor pressure, P*,
is tc*=1/Πpe. Using the dimensionless solution, the behavior of P* can be explored for a large range of values for Πpe. To recover the
dimensional solution for a particular value of Πpe, simply substitute, 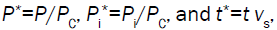 into the dimensionless solution
Equation 7 to obtain Equation 8.
into the dimensionless solution
Equation 7 to obtain Equation 8.
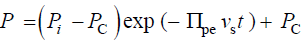 (8)
(8)
Note that, 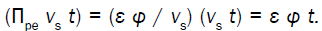 Equation 8 is the same solution previously obtained for a stress relaxation
experiment [11,15,18]. Other expansive growth behavior and experimental results can be described using modified versions of the
dimensionless augmented growth equations (Equations 4-6). Their dimensionless solutions can be used to explore a large range
of parameter magnitudes using the inclusive dimensionless groups.
Equation 8 is the same solution previously obtained for a stress relaxation
experiment [11,15,18]. Other expansive growth behavior and experimental results can be described using modified versions of the
dimensionless augmented growth equations (Equations 4-6). Their dimensionless solutions can be used to explore a large range
of parameter magnitudes using the inclusive dimensionless groups.
It is apparent that new dimensionless groups can be obtained by taking products or ratios of the dimensionless groups obtained from the dimensionless Augmented Growth Equations. For example, Πpw can be obtained from the ratio, Πpv/Πwv=Πpw=φ/ L=(relative volumetric plastic deformation rate of the wall)/(relative volumetric water uptake rate). The magnitude of Πpw is useful because when it is small (Πpw << 1), it means that water uptake rate is not limiting during expansive growth and Equation 2 or Equation 5, is the sole governing equation that determines the relative volumetric growth rate [15].
Traditionally in the physical sciences, dimensionless groups are used to organize and analyze large quantities of data from experiments and tests [20]. Because dimensionless groups already provide functional relationships between inclusive variables, it takes fewer graphs between relevant Π parameters to determine the functional relationship between all the variables involved in the process [20]. The Π parameters obtained from the dimensionless augmented growth equations can be used to organize data related to expansive growth of walled cells. One dimensionless group that is particularly interesting is Πpe. This dimensionless group reflects the constitutive (stress-strain) relationship of the growing cell wall, which in turn reflects wall loosening and wall hardening characteristics of the wall chemistry used to regulate the wall mechanical properties and wall deformation behavior. Some published data is available to evaluate Πpe. It is noted that nearly all of the relevant published research assumes that changes in volume occur predominately by changing the length of the cell, the diameter is assumed to remain relatively constant. Elongation growth rate data obtained from published research is used to evaluate Πpe, i.e. Πpe = (ε φ / vs). Data is obtained [15-18] and used to estimate Πpe for plant cells in pea stems [15] (pe ≈ 32), internode algal cells [16,17] (Πpe ≈ 564), and fungal sporangiophores [18] (Πpe ≈ 1615); please see analyses, estimates, and definitions for details. It is noted that the respective magnitudes are different by an order of magnitude or more. These values indicate that the ratio of plastic and elastic wall deformation rates of internode algal cells of Chara corallina is much larger than that of plant cells in pea stems (Pisum satinis L.), but much smaller than that of fungal sporangiophores of Phycomyces blakesleeanus. It is suggested that the different magnitudes of Πpe for these different cells reflect different chemorheology in their respective walls, i.e. it reflects different wall chemistry that produces wall loosening and wall hardening which controls the wall mechanical properties and wall deformation behavior. This suggestion would predict that the wall chemistry is different for plant cells in pea stems of P. satinis L., internode algal cells of C. corallina, and fungal sporangiophores of P. blakesleeanus. There is evidence supporting this prediction. In a variety of higher plant cells within tissue, a pH-dependent protein (expansin) is found to loosen the wall by disrupting the hydrogen bonds between microfibrils [5,8]. In large internode algal cells of C. corallina, experimental evidence indicates that making and breaking calcium bridges between pectin polymers loosens and hardens the wall [9,10]. It is not known how the sporangiophore of P. blakesleeanus loosens and hardens its wall [2-4], but this suggestion would predict that its chemorheology and wall chemistry will be different from those used by either plant cells in pea stems of P. satinis L. or internode algal cells of C. corallina.
Although the global augmented growth equations have proven to be very useful, in general global equations have limitations. Local mathematical biophysical models [14,21,22] for the cell wall are needed to describe wall deformation behavior during helical growth [23-25], oscillatory cell growth [26,27], cellular bending [2,7] and morphogenesis [7,28-31]. The dimensionless augmented growth equations and inclusive Π parameters can guide the construction of future local mathematical biophysical models to ensure that the ratios of important processes (e.g. plastic and elastic deformation rates) are the same. For example, wall deformation similarity may be established by matching the Πpe of the local mathematical model to the Πpe obtained experimentally.
Dimensionless variables
The variables in Equations 1-3 are made dimensionless (*) with the following constant reference parameters: PC (critical turgor pressure), vs (steady relative volumetric growth rate), and vsT (steady relative volumetric transpiration rate).
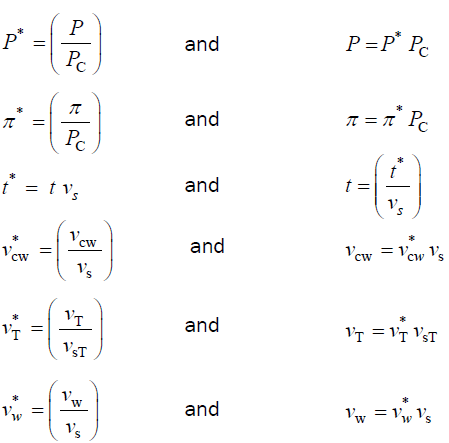
Dimensionless equations
Substituting the respective expressions that includes the dimensionless variable and reference parameter (variables and their respective expressions in the right column above) for each of the variables into Equations 1-3, we get
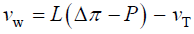 (1)
(1)
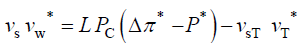
and
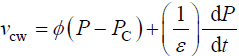 (2)
(2)
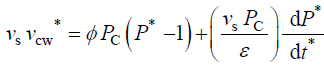
and
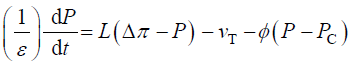 (3)
(3)
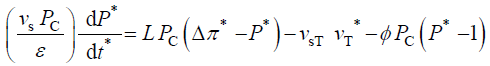
Dividing first two equations by the constant reference parameter, vs, and dividing the third equation by the constant coefficient, vs Pc /ε, we get
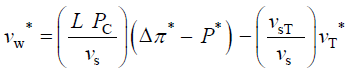 (4)
(4)
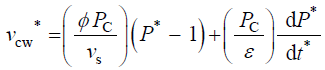 (5)
(5)
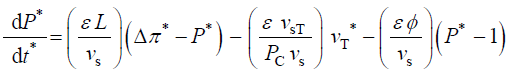 (6)
(6)
Estimates for Πpe
The magnitude of Πpe = (ε φ / vs) is estimated for pea stems, internode algal cells, and fungal sporangiophores.
The following values were obtained for pea stems, Pisum satinis L. [15].
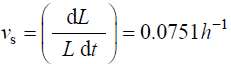
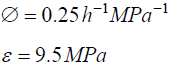
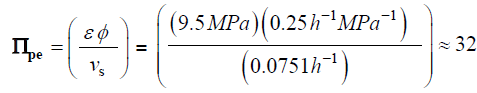
The following values were obtained for algal cells, Chara corallina [16,17]
L = 13mm = 1.3×104μm
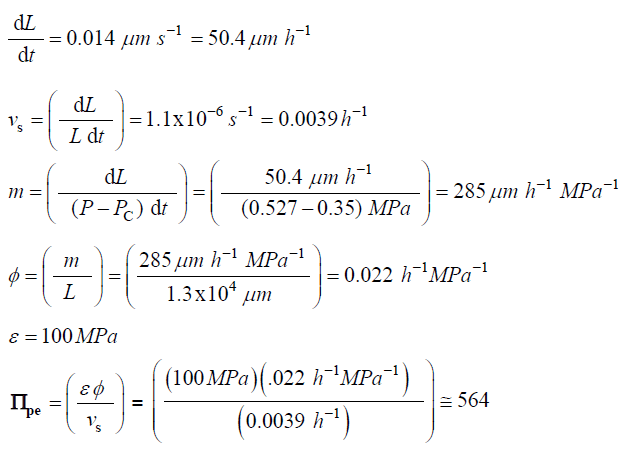
The following values were obtained for fungal sporangiophores of Phycomyces blakesleeanus [18].
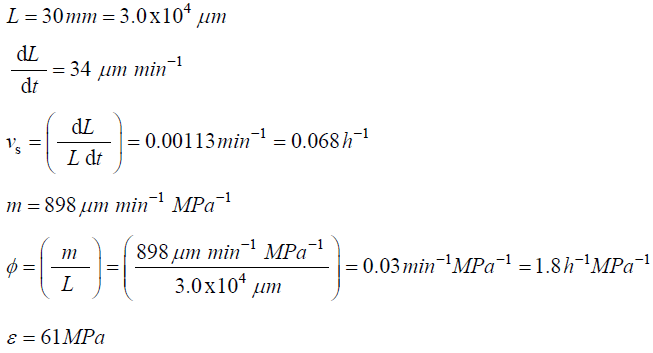
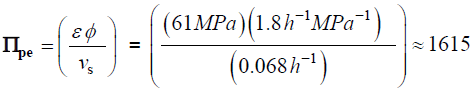
Definition of variables and terms
A = area of the plasma membrane
LP = hydraulic conductivity of the plasma membrane
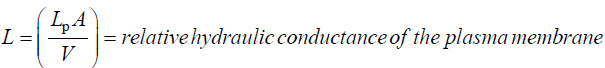
P = turgor pressure (gage pressure relative to atmospheric pressure)
PC = critical turgor pressure (to be exceeded before plastic deformation occurs)
t = time
V = volume
Vcw = volume of cell wall chamber
Vw = volume of water in the cell
VT = volume of water lost by transpiration
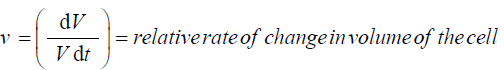

ε = volumetric elastic modulus
φ = relative irreversible extensibility of the cell wall
Δπ = osmotic pressure difference across the plasma membrane
L(Δπ – P) = relative volumetric rate of water uptake
φ(P – PC ) = relative volumetric plastic deformation rate of the cell wall
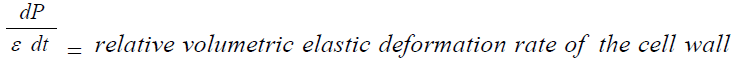
This research was support by NSF Grant, MCB-0948921, to J.K.E. Ortega.