Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Direct Instantaneous Torque Control of Switched Reluctance Motors

D.A.Shahakar1, V.M.Jape2
  1. M.Tech Scholar, Department of Electrical Engineering, Government College of Engg., Amravati, Maharashtra, India
  2. Asst. Prof., Department of Electrical Engineering, Government College of Engg., Amravati, Maharashtra, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The main disadvantage of switched reluctance motors (SRM) is the higher torque ripple compared to conventional machines, which result in acoustic noise and vibration. The torque pulsations in an SRM are due to the highly non-linear and discrete nature of torque production mechanism. The paper presents an investigation on the direct instantaneous torque control (DITC) of a 1-hp four-phase 8/6 switched reluctance motor (SRM). In the proposed technique, direct instantaneous torque control for a four-phase SRM drive the torque sharing function can be used to generate the reference values of phase torques from the required torque. The switching signals are directly generated from the comparison between the reference phase torques and the estimated phase torques using hysteresis controller. The hysteresis torque controller generates gating signals to the power converter. The instantaneous phase torques can be calculated from the phase currents and rotor position. Therefore, a high-resolution encoder can be avoided. Results obtained from computer simulations of the developed MATLAB / Simulink model experiments have confirmed the validity and acceptable performance of the proposed scheme.

Keywords
Switched reluctance motor, Torque ripple minimization, Direct instantaneous torque control

INTRODUCTION
Switched reluctance motors (SRM) have many advantageous characteristics comparing to those of the conventional AC and DC machines. The mechanical simplicity in construction of the SRM can be seen through their purely laminated-steel structure without permanent magnets, rotor windings and squirrel-cage bars. Thus, SR machines offer high reliability and robustness in operation. Due to their ruggedness, the SR motors are inherently suitable for high-speed drives and applications in high-temperature and hazardous environments. In addition, the SRM are efficient and suitable for some applications which required high torque and high dynamics. Consequently, the switched reluctance motors have recently gained a considerable attention from industries and researchers in the specific areas of high-performance and adjustable speed drives. Nevertheless, SRM are very nonlinear in nature due to their operations in high-saturation conditions. The highly non-uniform reluctance torque is produced from magnetic saliency between stator poles and rotor poles. Phase flux linkages and instantaneous phase torque are nonlinear functions of phase currents and rotor positions. Therefore, without proper control, the inherent torque ripples, vibrations and acoustic noise can become major problems of the SRM drives. For a century, such drawbacks have prevented the SR motors from being widely used in applications of high-quality and variable speed drives. With the view to achieve high-performance servo drives for SRM, several instantaneous torque control techniques including torque ripple minimization features have been successively proposed.
In the conventional scheme called indirect instantaneous torque control (IITC), SRM torque is regulated by controlling the instantaneous phase currents in a cascaded fashion. The reference torque is converted to equivalent reference phase currents so that they can be tracked in the inner current control loops. By using the phase current profiling technique, optimal phase torques corresponding to torque sharing functions can be generated and, ultimately, torque ripples can be minimized. Various methods of torque ripple-minimization using IITC have been successively proposed in the last three decades. [1]However, torque-to-current conversion in SRM is complex and becomes nontrivial due to their nonlinear relationship. Analytical expression of such conversion is complicated and leads to intensive on-line computation. On the other hand, the current profiles can be pre-calculated and pre-stored in the controller memory. Yet, this method requires large amount of on-line memory space. Concepts of direct instantaneous torque control (DITC) for SRM have been developed to overcome the mentioned drawbacks of the IITC. The main DITC characteristics are: the instantaneous torque (which can be estimated from motor terminal quantities) is considered directly as a control variable, torque-to-current conversion and closed-loop control of phase currents are no longer required. In other words, DITC does not use current or torque profiles. Therefore, DITC is expected to counteract the torque error instantaneously with fast dynamic response and effectively minimize the inherent torque ripple. A DITC for SRM using the concept of a short flux pattern that links two separate poles of the stator was already proposed.But this method was expensive and inconvenient, as it involved motor winding alteration and bipolar current requirement.The purpose of this paper is to present a simplified direct instantaneous torque control for a four-phase SRM drive. The torque sharing function can be used to generate the reference values of phase torques from the required torque. The switching signals are directly generated from the comparison between the reference phase torques and the estimated phase torques using hysteresis controller. The hysteresis torque controller generates gating signals to the power converter. The instantaneous phase torques can be calculated from the phase currents and rotor position.

DEVELOPMENT OF TORQUE
The most general expression for the torque produced by one phase at any rotor position is,
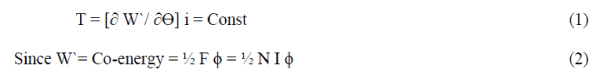image
This equation shows that input electrical power goes partly to increase the stored magnetic energy (½L* i2) and partly to provide mechanical output power ( i2/ 2 x dL /dÓ¨ x ω ), the latter being associated with the rotational e.m.f. in the stator circuit. Neglecting saturation non-linearity
image
This equation shows that the developed torque is independent of direction of current but only depends on magnitude of current & direction of dL/dÓ¨.
The Fourier Series of phase winding inductance is given by
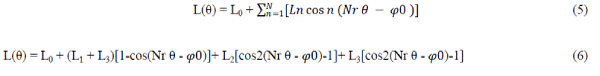image
Where L0 =Lmin, Lmin is the minimum phase winding inductance;
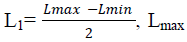image is the maximum phase winding inductance; L2 and L3 are the coefficients of absolute pole width and relative pole width of stator-rotor respectively.
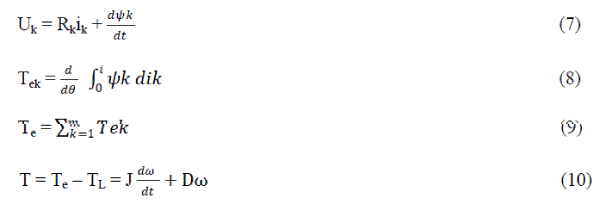image
where Uk, Rk, ikandψk are voltage, resistance, current, and flux linkage of the phase winding respectively; θ is rotor position angle; ω is rotational velocity; Tek and Te are electromagnetic torque of phase winding and SRM respectively; m is the number of phase; TL is load angular force; D is viscous friction coefficient; is moment of inertia of rotor and load of SRM.
image
Variation in rotor position with respect to time results in angular speed.
Hence theta is associated with ω as a function of time.

TORQUE SHARING FUNCTIONS
At any, time the resultant output torque of SRM is the summation of the torque in all phases. If the phase current is fixed, the torque of an 8/6 SRM will have a profile as shown in Fig.1
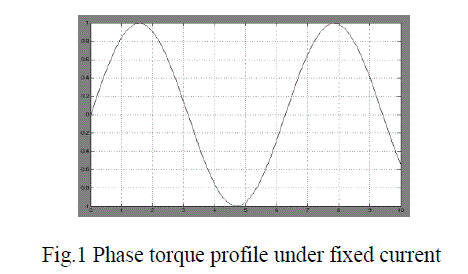image
From Fig.1, it is clear that high torque is not available near aligned/unaligned position even when high phase current is presented. To generate a ripple –free output torque, there must be overlapping between phases. During phase overlapping, the current in one phase is increasing. To obtain a constant torque, the summation of the torque generated in non-overlapping period. To determine the desired torque produced by each phase, torque sharing functions (TSFs) are introduced, which are defined as
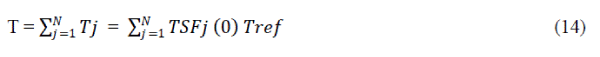image
Where TSFj(θ) is the torque sharing function for phase j at rotor position θ, and Tref is the reference torque. For four phase 8/6 switched reluctance motor, to generate desired torque, the torque sharing functions must meet the following requirements:
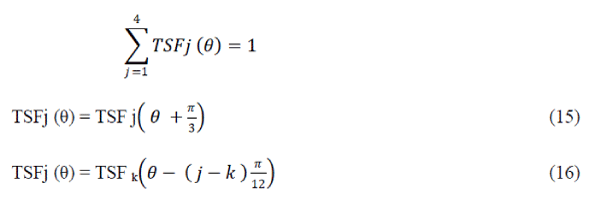image
For 8/6 SRM, the inductance increasing/decreasing period for each phase will be π/6 and the conduction angle to be selected as π/8. This means
image
so the phase overlapping for each two adjacent phase is π / 8 – π / 12 = π / 24.
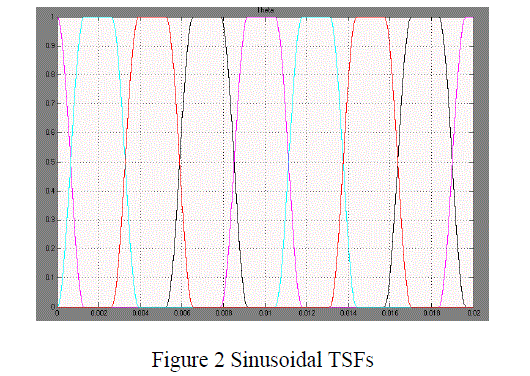
For this work, a sinusoidal torque sharing functions can be used. The sinusoidal torque sharing functions means that the torque produced by the phases, during phase commutation, changes with the rotor position in terms of the sinusoidal functions. On the basis of the sinusoidal torque sharing function presented by Husain and Ehsani, the sinusoidal torque sharing function for phase j in a rotor period can be expressed as
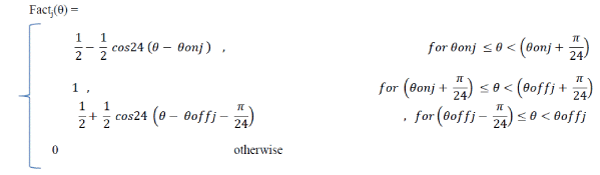image
The Figure 2 shows the sinusoidal torque sharing functions of all four phase in forward motoring operation.
image

DIRECT INSTANTANEOUS TORQUE CONTROL OF SRM
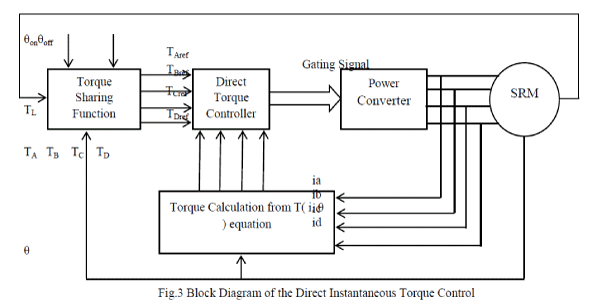
The block diagram of the direct instantaneous torque control is shown in fig.3. First, the phase torques are calculated from the measured phase currents and rotor position using the torque. The magnitude of the reference phase torques can be calculated using the torque sharing functions. The input reference phase torques will be compared with the feedback estimated phase torques using hysteresis controller. The hysteresis controller outputs three discrete voltage levels + Vdc, 0, - Vdc will be applied to the motor.
The justification of using applied phase voltage to directly control the instantaneous torque of switched reluctance motor is explained here.
The nonlinear instantaneous torque of SRM can be found co energy principal, as expressed in equation (2) earlier. For simplification, the torque equation becomes
image
Thus, the instantaneous torque of the saturated SRM can be found from the product of the flux linkage derivative (with respect to rotor position) and the phase current, as shown in equation (18).
The phase voltage equation of SRM is given by
image
This incremental inductance I(i, θ) has significantly large value such that phase current can be assumed unchanged in one sampling period. Once the resistive drop is negligible and the current is considered constant, the phase voltage equation can be approximated as equation (20)
image
Consequently, the instantaneous phase torque equation of SRM can be simplified to:
image
The rotor speed and the phase current are assumed constant during the control cycle. As a result, the torque expression has been linearized and the phase voltage V becomes an effective control variable for the DITC.
image

Result
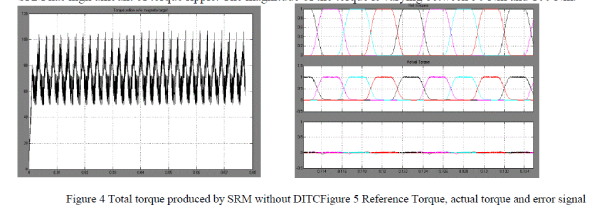
The proposed scheme is implemented and simulated in the Mtlab/Simulink for a four phase switched reluctance motor with 8 stator poles and 6 rotor poles. Figure 4 describes the total torque produced by SRM without torque control for turn –on angle θon = 30º, turn-off angle θoff = 52.5º, constant speed N = 700 rpm and a current reference of Iref = 12 A with hysteresis current control. From figure 4 it is clear that the total torque produced by the SRM has high amount of torque ripple. The magnitude of the torque is varying between 50 Nm and 100 Nm.
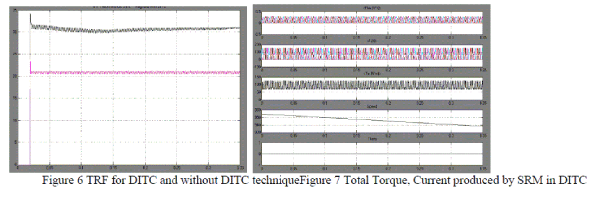
image
Figure 5 shows the comparison of torque ripple factor for DITC and without DITC technique.
Results of flux, current, torque, speed and theta for individual phase is shown. At θon = 30, as voltage is applied, current starts to increase and at the point of θoff , voltage becomes zero and current starts to decrease. For positive motoring torque, current should be in the range of positive growing inductance, as shown in fig.7 Phase current and total current waveforms are shown in fig 7 and fig 7 respectively.
image

CONCLUSIONS
This paper proposes a simple method of direct instantaneous torque controller for SRM. It overcome the drawbacks of the indirect instantaneous torque control (IITC) schemes like complexity in torque to current conversion and the requirement of large memory space for storing the current values corresponding to torque and all positions. In this method, the phase torques are calculated from the measured phase current and rotor position. The magnitude of reference phase torque is calculated using torque sharing functions. The input reference phase torques are compared with the feedback estimated phase torques using hysteresis torque controller. The hysteresis torque controllers have three discrete voltage levels outputs which are to be applied to the motor. As the instantaneous torque is considered directly as a control variable, DITC encounter the torque error instantaneously with fast dynamic response and effectively minimize the inherent torque ripple. The DITC scheme also eliminates the use of current controllers. With the implementation of proposed direct instantaneous torque control (DITC) scheme, the torque ripple factor (TRF) of SRM is reduced. Simulation results really validate the applicability of the proposed direct instantaneous torque control scheme.
 

References