Keywords
|
| Fuzzy logic, IM, DTC, DTFC, switching table |
INTRODUCTION
|
| Direct torque control was presented by Manfred Depenbrock 1984. He called it "Direct Self-Control" (DSC). The only difference between DTC and DSC is the shape of the path along which the flux vector is controlled to follow. In DTC the path is a circle and in DSC it was a hexagon. Today DTC uses hexagon flux path only when full voltage is required at high speeds. Since Depenbrock, Takahashi and Noguchi had proposed direct torque control (DTC) for induction machines in the mid 1980s, this new torque control scheme has gained much momentum. From its introduction, the Direct Torque control or Direct Self Control (DSC) principle has been used for Induction Motor (IM) drives with fast dynamics. Despite its simplicity, DTC is able to produce very fast torque and flux control, if the torque and flux are correctly estimated. Induction motor (IM) Direct Torque Control (DTC) is based on the electromagnetic torque and stator flux hysteresis controls [1,2]. The conventional DTC method has various attractive advantages, but also some shortcomings [2]. Fuzzy logic is recently getting increasing emphasis in soft computing applications in the recent days. Hence, the development of high-performance control strategies for AC motor drives resulted in a rapid evolution. One of the most popular methods, known as field oriented control has been proposed by F. Blaschke[7] has disadvantages like inclusion of the pulse encoder, indirect torque control and also it is quite complex due to reference frame transformations. To overcome these disadvantages, in the middle of 1980’s, a new quick response technique for the torque control of induction motors was proposed by Takahashi as direct torque control [2]. DTC provides very quick response with simple control structure and hence, this technique is gaining popularity in industries [3]. Though DTC has high dynamic performance, it has few drawbacks such as high ripple in torque, flux, current and variation in switching frequency of the inverter. To improve the performance of conventional DTC, modern resources of artificial intelligence like neural networks, fuzzy logic and genetic algorithms are implemented [4]. In the following, we will describe the application of fuzzy logic in DTC [5, 6]. |
PRINCIPLE OF CONVENTIONAL DTC
|
| DTC principle is widely employed for induction motor drives with fast dynamics [6]. The main notion of the conventional DTC is the rate of change of torque is proportional to the instantaneous slip between the stator flux and rotor flux under constant stator flux linkage [5]. DTC has been widely recognized for its fast and robust torque and flux control. The rotor flux linkage changes slowly compared to the stator flux linkage, as the rotor time constant of a standard squirrel-cage induction machine is very large. However, the rotor flux is almost unchanged during a short transient. Thus rapid changes of the electromagnetic torque can be produced by rotating the stator flux in the required direction, as directed by the torque command. On the other hand the stator flux can instantaneously be accelerated or decelerated by applying proper stator. Thus, the simultaneous and decoupled control of torque and flux is achieved by direct adjustment of the stator voltage in response to the torque and flux errors [9]. The DTC regularly applies the appropriate voltage vector in order to maintain the torque and stator flux within two hysteresis bands which results bangbang behavior and produces variation in witching frequency and significant ripple in flux, torque and current [8]. |
DTFC WITH VOLTAGE SOURCE INVERTER
|
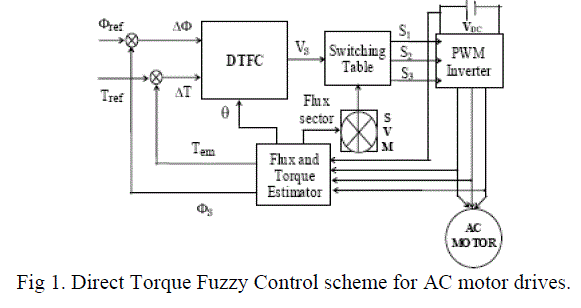
| The schematic of the basic functional blocks used to implement the proposed DTFC of induction motor drive is shown in Fig.1. A voltage source inverter supplies the motor and instantaneous values of the stator flux and torque are calculated from stator variable by using a closed loop estimator [3]. Stator flux and torque can be controlled directly and independently by properly selecting the inverter switching. |
 |
| The mathematical model for a three-phase Y-connected squirrel-cage IM in a de-qe synchronously rotating reference frame is described in (1)-(4). |
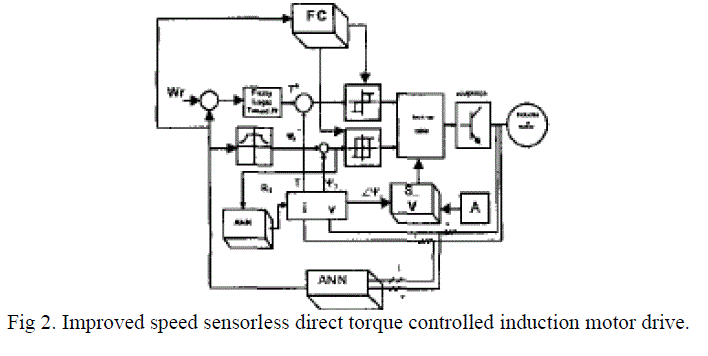
| The schematic of the basic functional blocks used to implement the DTFC of induction motor AC drive is shown in Fig.1. A voltage source inverter supplies the motor and instantaneous values of the stator flux and torque are calculated from stator variable by using a closed loop estimator [2]. Stator flux and torque can be controlled directly and independently by properly selecting the inverter switching. In Fig.3 shows the conventional IM DTC method with an artificial neural network (ANN) speed estimator, a fuzzy controller (FC) for the inverter switching frequency regulation that adjusts the hysteresis band amplitudes in the flux and torque control loops, a variable switching sector block (S-V) for shifting the sectors in the DTC method; the block (A) fixes the value of angle that rotaries the sectors in the complex plane, a fuzzy system to tune the proportional and integral gains of the PI speed controller, and an ANN that estimates the stator resistance. |
 |
| A) Vector Model of Inverter Output Voltage |
| The space vector modulation (SVM) technique is used to approximate the voltage vector by employing the one out of eight possible combinations of vectors generated by 3- Φ phase voltage source inverter for AC motor drives. In a 3-Φ, voltage source inverter, the switching commands of each limb are complementary. So, for each limb, logic state Si (where i=1 to 3) is ON (“1”) or OFF (“0”) can be defined. As there are three independent limbs, there will be eight different logic states, provides eight different voltages obtained applying the vector transformation described as: |
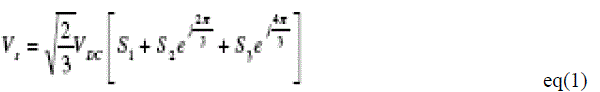 |
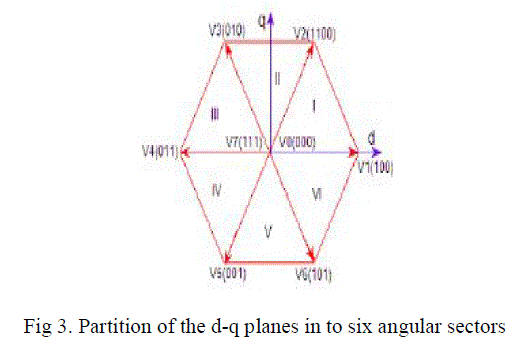
| Eight switching combinations can be taken according to the above expression (1). The partitions of d-q plane in to two zero voltage vectors and six non-zero voltage vectors are show in Fig.3. |
 |
| B) Stator Flux and Torque Estimation Mechanism |
| The components of the current (Id, Iq) and stator voltage (Vd, Vq) are obtained by the application of the transformation [3] expressed in (2) and (3). The components of the stator flux (d, q) are expressed in (4). The stator flux linkage per phase and the electromagnetic torque estimated are expressed in (5) and (6) respectively. |
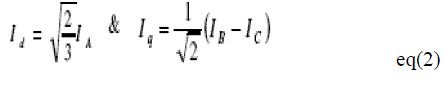 |
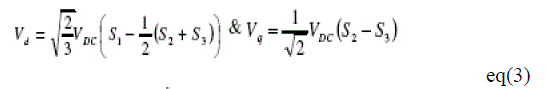 |
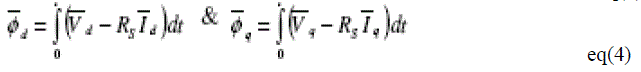 |
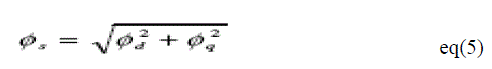 |
 |
| The stator resistance RS can be assumed constant during a large number of converter switching periods TS. The voltage vector applied to the induction motor remains also constant over the time period TS. Therefore, on resolving (1) leads to: |
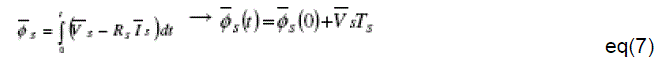 |
| In equation (7), φ S(0) stands for the initial stator flux condition. This equation shows that when the term RSIS can be neglected in high speed operating condition of the extremity of stator flux vector VS. Also, the instantaneous flux speed is only governed by voltage vector amplitude [3] expressed in (8). |
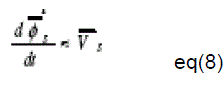 |
| Hence, by selecting adequate voltage vector one can increase or decrease the stator flux amplitude and phase to obtain the required performances with constant flux Φ S [3] [5]. |
| C) Switching Table Formation |
| The vectors Vi+1 or Vi-1 are selected to increase the amplitude of flux, and Vi+2 or Vi-2 to decrease it when flux is in sector I. Which shows that the choice of the vector tension depends on the sign of the error of flux is independent of its amplitude [3]. Obviously, the exit of the corrector of flux must be a boolean variable. One adds a band of hysteresis around zero to avoid unwanted commutations when the error of flux is very small [3] [4]. Indeed, with this type of corrector in spite of its simplicity, one can easily control and maintain the end of the vector flux in a circular ring form. The switching table proposed by Takahashi [3] is as given in Table I. |
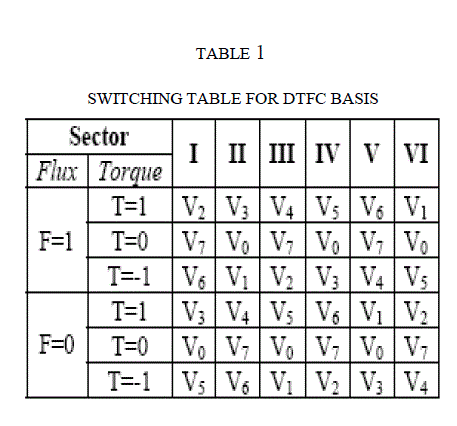 |
PRINCIPLE OF DIRECT TORQUE FUZZY CONTROL
|
| The DTFC of induction motor drive is designed to have three fuzzy input variables and one output control variable to achieve fuzzy logic based DTC of the induction machine [7] [8]. Its functional block diagram is as shown in Fig.4. |
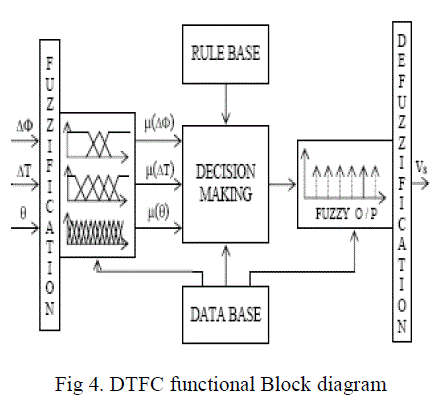 |
| It requires three input variables, the stator flux error, electro magnetic torque error and angle of stator flux. The output is the voltage space vector. The proposed DTFC consists of fuzzification, rule base, data base, decision making and defuzzification blocks as shown in Fig.4. The input variables ΔÃÂä, ΔT and θ are fuzzyfied using fuzzy functions over the respective domains. The output of DTFC is also fuzzyfied using fuzzy singletons. The all possible fuzzy rules are stored in fuzzy rule base. DTFC takes the decision for the given input crisp variables by firing this rule base. |
RESULT OBSERVATION
|
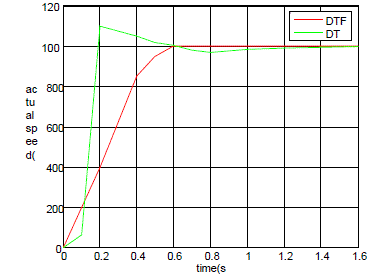 |
| Fig 5. DTC and DTFC actual speed simulated responses as can be seen DTF and DT performance there is a quick stability in DTF mode were as a sudden peak can be noticed in DT. |
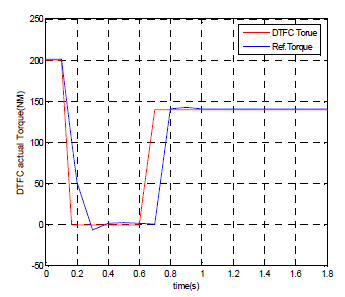 |
| Fig 6. DTFC torque simulated response can be seen here the red line indicating the DTFC torque control with respect t time |
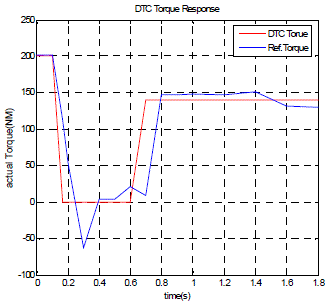 |
| Fig7. Conventional DTC torque simulated response indicating DTC torque with correspond to actual torque depicted by red and blue line respectively. |
CONCLUSION
|
| The paper presents a new approach for speed control of 3-Φ induction motor using fuzzy logic in DTC scheme. This methodology for AC drive systems is intended for an efficient control of the torque and flux without changing the motor parameters. Also the flux and torque can be directly controlled with the inverter voltage vector using SVM methodology. The simulation study clearly indicates the superior performance of DTFC over conventional DTC, because it is inherently adaptive in nature. To make this DTFC AC drive system fully adaptive, the hybridization of fuzzy with other soft computing techniques like ANN and Rough Sets will be preferred. |
| |
References
|
- P. Vas, “Sensorless Vector and Direct Torque Contml”.Oxford University Press. 1998.
- M. P. Karmierkowski, ‘Control Strategies for PWM Rectifierlhvener- Fed QductionMoton”. hPrac. ISE’2000 Conf..vol.I , pp. 15-23.2000.
- P. Tiitinen, M. Surandra, “The next generation motor control method, dtc direct torque control”, Proceedings on Power Electronics, Vol. 1, pp: 37–43, 1996.
- Hui-Hui Xiao, Shan Li, Pei-Lin Wan, Ming-Fu Zhao, _Study on Fuzzy Direct Torque Control System_, Proceedings of the Fourth International Conference on Machine Learning and Cybernetics, Beijing, pp: 4-5 August 2002.
- R.ToufoutiS.Meziane, H. Benalla, “Direct Torque Control for Induction Motor Using Fuzzy Logic”, Proc. ACSE Journal, Vol. 6, Issue 2, pp:19 – 26, Jun. 2006.
- S. Benaicha, R. Nait-Said, F. Zidani, M-S.Nait-Said, B. Abdelhadi, “A direct torque fuzzy control of SVM inverter-fed Induction Motor drive”, Proc. of the International Journal of Artificial Intelligence and Soft Computing Vol. 1, Nos. 2-4, pp: 259 – 270, 2009.
- F. Blaschke “The principle of field orientation as applied to the new TRANSVECTOR closed loop control system for rotating field machines”, Siemens Review XXXIX, (5), pp:217–220, 1972
- D. Casadei, G. Grandi, G. Serra, A. Tani ”Effectes of flux and torque hysteresis band amplitude in direct torque control of induction machines”, IEEE-IECON-94, 1994, 299–304.
- Hui-Hui Xiao, Shan Li, Pei-Lin Wan, Ming-Fu Zhao, ″Study on Fuzzy Direct Torque Control System″, Proceedings of the Fourth International Conference on Machine Learning and Cybernetics, Beijing, 4-5 August 2002.
- S. Benaicha, R. Nait-Said, F. Zidani, M-S.Nait-Said, B. Abdelhadi, “A direct torque fuzzy control of SVM inverter-fed Induction Motor drive”, Proc. of the International Journal of Artificial Intelligence and Soft Computing Vol. 1, Nos. 2-4, pp. 259 – 270, 2009.
- Hui-Hui Xia0, Shan Li, Pei-Lin Wan, Ming-Fu Zhao, ″Study on Fuzzy Direct Torque Control System″, Proceedings of the Fourth International Conference on Machine Learning and Cybernetics, Beijing, pp. 4-5 August 2002.
|