In this paper, Fuzzy concept hierarchies are used for multi-level association rule mining from large datasets via Attribute-Oriented Induction approach [1]. In this the process of fuzzy hierarchical induction approach is used and extends it with two new characteristics which improve applicability of the original approach in data mining. The proposed drilling-down approach of fuzzy induction model allows user to retrieve estimated explanations of the generated abstract concept. An application to discovery of multi-level association rules from environmental data stored in a Toxic Release Inventory is presented.
Keywords |
| Fuzzy Hierarchies, Propogation, Association Rules |
INTRODUCTION |
| The need for generalization mechanisms has been proven to be a critical factor for many data mining tasks. To
efficiently analyze voluminous data sets, which are currently stored in databases of almost all companies, it is often
necessary to start from pruning and reducing of the size of these repositories. |
| Decision makers are usually not interested in time consuming extraction of technical details (i.e. serial numbers, time
of transactions with precision in seconds, detailed GPS locations, etc.) stored originally in large databases. Instead, they
want to obtain knowledge at a certain level of abstraction, as dictated by their professional goals or by the character of
the analysed dataset. The data conceptually represent information at multiple levels . For instance, an item, represented
by a bar code: 040101000 is a Milky Way Bar, which is a Chocolate Bar, pertaining to a Snack, or even a Food group,
etc. |
| Attribute-Oriented Induction (AOI) [1] allows compression of the original set of data into a generalized relation to
provide data analysts with concise and summarize information about the original, massive set of task-relevant data. The
AOI process employs background knowledge represented in the form of concept hierarchies, separately declared for
each of the attributes in the analyzed database table. |
| Induction of the original relation is performed one step at a time on an attribute-by-attribute basis. The method has
rather straightforward character [1]: |
| (1) Gather task-relevant data into the initial relation |
| (2) Generalize the data by removal or generalization of derived attributes. An attribute can be removed if it has a
large set of distinct values and no generalization hierarchy for the attribute is available or if the abstract concepts are
reflected by other attributes in the initial relation. Attribute values can be generalized if a concept hierarchy for them
has been defined. |
| (3) Aggregate the data by merging identical tuples and accumulating their respective counts. New attribute COUNT
has to be added to the relation, to keep track of original records, which are gradually merged during the transformation
of attribute values from one level of abstraction to another. Value stored in the COUNT column reflects the number of
original records merged together into a generalized tuple. |
| (4) Present generated (generalized) table to the user. Additional data mining algorithms can be further applied on this
relation. |
| The hierarchical character of AOI provides analysts with ability to view the original information at multiple levels of
abstraction, allowing them to progressively discover interesting data concentration points. In contrast to the flat
summarization a gradual process of attribute-oriented induction through concept hierarchies allows detailed tracking of all records, and can lead to the discovery of interesting patterns among data at the lowest abstraction level of their
occurrence. In the AOI approach the tuples, which initially (at a low level of abstraction) do not match the requirement
of minimum support assigned to eliminate seldom occurring regularities, rather than being dropped, are gradually
further aggregated and so given a chance to reach a meaningful count at a higher abstraction level. Such an approach
improves accuracy of generalization, since now only those records that are truly infrequent at each of the abstraction
levels are eliminated from further analysis. |
RELATED WORK |
| The idea of applying concept hierarchies to generalize database records was proposed by Han [1-4] and developed
further by other researchers [5-6]. Recently, Hsu [7] extended the basic AOI algorithm for generalization of numeric
values. The majority of the mentioned work focuses on attribute oriented induction with utilization of crisp concept
hierarchies where each attribute value can have only one direct abstract to which it fully belongs. |
| However, regular concept hierarchy are not the best representation for usually complex dependencies occurring in
the attribute domains due to their crisp character. Recently several independent groups of researchers have investigated
applications of a fuzzy concept hierarchy to AOI. Lee and Kim [8] used fuzzy ISA hierarchies, from the area of data
modelling, to generalize database records to more abstract concepts. Lee [9] applied fuzzy generalization hierarchies to
mine generalized fuzzy quantitative association rules. Cubero, Medina, Pons, and Vila [10] presented fuzzy gradual
rules for data summarization. Raschia, and Mouaddib [11] implemented the SaintEtiq system for data summarization
through extended concept hierarchies. |
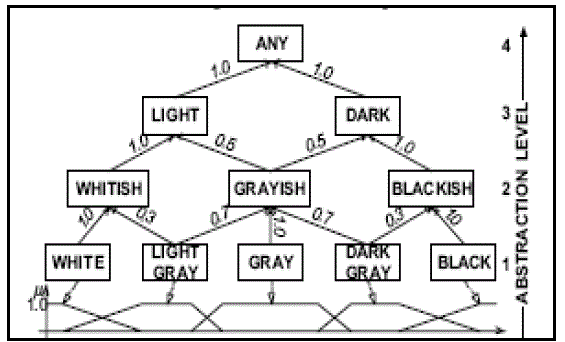
| Fuzzy concept hierarchies (Figure 1) seem to better capture human approaches to induction. Trivi al examples
supporting this conclusion can be found everywhere, e.g. how to generalize three colors, such as black, gray and white
to two abstract terms: dark, light, or to which continent should we assign the Russian Federation, taking under
consideration a fact that almost one fourth of this country lies west of the Urals. In fuzzy concept hierarchies, lower -
level concepts can belong to more than one descriptor placed on the directly higher level of abstraction. Unfortunately,
none of the above-mentioned fuzzy induction models focuses on guaranteeing the preservation of exact dependencies
among low-level (original) tuples after transforming them to more general descriptors. |
FUZZY CONCEPT HIERARCHIES FOR THE ATTRIBUTE-ORIENTED INDUCTION |
| The main difference between a crisp concept hierarchy and a fuzzy one is the type of generalization relation between
the concept and its direct abstract these structures are capable of modeling. In crisp hierarchies, each lower-level
concept is fully assigned to only one direct abstract, and a single abstract can have many direct specializes. In fuzzy
concept hierarchies a generalization relation is allowed to have a many-tomany character; a single lower-level concept
can have multiple abstracts at the next abstraction level, related to each of these concepts to a different extent. |
| Our fuzzy concept hierarchy is an augmented rooted tree structure. Each link l in the fuzzy concept hierarchy is a
bottom -up directed arc (edge) between two nodes (i.e. concepts) with a certain weight assigned to it. Such a structure
reflects a fuzzy induction triple. |
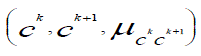 , where , where 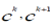 are endpoints of are endpoints of 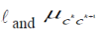 represents the strength of conviction that
the lower-level concept represents the strength of conviction that
the lower-level concept 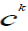 should be qualified as concept should be qualified as concept 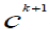 when the data generalization process moves to the next
abstraction level. During AOFI the value of when the data generalization process moves to the next
abstraction level. During AOFI the value of 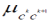 dictates what fraction of a vote, representing original attribute
values generalized already to the concept dictates what fraction of a vote, representing original attribute
values generalized already to the concept 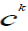 ck, is propagated to its higher-level representation ck, is propagated to its higher-level representation 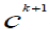 |
| A. Consistency of Vote Propagation And Completeness Of The Model |
| Other approaches to the attribute-oriented fuzzy generalization do not concentrate on precise and consistent
preservation of all original dependencies among the data at each level of induction. It limits their usage in many data
mining projects, which perform exhaustive analysis of scientific data. To guarantee exactness of the data
summarization via AOFI we need to preserve the number of original tuples and the relation between them in the
identical proportions at each level of abstraction. In other words, to provide a consistent AOFI we need to assure that
each record from the original database relation will be counted exactly once at each of the levels of the AOI hierarchy.
We call this an exact vote propagation dilemma, which follows the vote propagation for crisp AOI. |
This problem can be resolved by preservation of completeness in an AOFI model. The fuzzy generalization
hierarchy is complete and consistent when for all adjacent hierarchy levels, 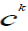 and and 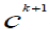 (where (where 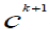 is a direct
abstraction level of is a direct
abstraction level of 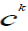 ), the following relationship is satisfied: ), the following relationship is satisfied: |
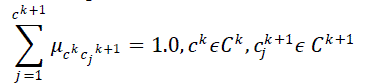 |
| In other words, the sum of weights assigned to the links leaving any single node in a fuzzy concept hierarchy needs
to be 1.0 for completeness of the AOFI model. |
| Preservation of the above property prevents any attribute value (or its abstract) from being counted more or less than
once at each step of the attribute-oriented fuzzy induction (i.e. consistency). It also guarantees that a set of abstracts
concepts at each level of hierarchy will cover all of the attribute values that occurred in the original dataset (i.e.
completeness of the model). So we are guaranteed to not lose correct count of the number of tuples when generalizing
their attribute values. |
| Such normalized representation of uncertainty, which is a common element of many generalization processes, should
not be confused with representation of probabilistic dependencies. First of all, fuzzy concept hierarchies do not reflect
probabilities with which lower-level concepts may be assigned to their direct abstracts – the hierarchies reflect actual
degrees with which the lower-level concepts belong to the generalized terms (allowing for more adequate reflection of
natural human reasoning). Secondly, the only purpose of hierarchy normalization in our approach is to assure accurate
representation of original tuples during the AOI process. Formally, each concept hierarchy (also the un -normalized
one) can be utilized to perform consistent and completeAOI. Normalization of hierarchy can be performed via simple
normalization of membership values in all outgoing links for every concept placed in the hierarchy. |
| B. Drilling Down Fuzzy Concept hierarchies To Provide Explanations Of Abstract Concepts |
| Since generalized tuples, which reached their count value above the minimal support threshold, may appear at
multiple levels of abstraction, a data analyst may want to drill down the definition of each of the reported generalized
descriptors. This can be achieved by recursive extraction of lower -level components of the abstract concept. |
| To obtain an explanation of what is behind a particular abstract concept, which characterizes a significant part of
original data set generalized to the related abstraction level, we backtrack the components (lower-level concepts) of the
concept. We are able to do so through the analysis of the induction paths, which were activated during AOFI and led to
the particular abstract. In general, such an explanation can be either (1) Simplified and based only on the background knowledge (only knowledge about activated generalization paths
from concept hierarchy is utilized) or have (2) a detailed, knowledge-driven, but data distribution based character
(when we preserve the count of votes grouped at each node during the AOI process). In both of the cases we utilize a
concept of ―descending memberships‖, which are derived from the original (i.e. ascending) membership values
included in the concept hierarchies and used during the AOFI. |
| The second approach has a more comprehensive character but requires more time for computations and considerably
larger memory for preservation of all intermediate data tables, generated during the AOI process. These characteristics
make it inapplicable for mining very large databases. |
| Approximate explanations are based only on the concept hierarchies and the generalized output table, requiring
much less memory than the original, massive dataset. |
| Using a concept hierarchy, we can explain each abstract concept by tracking down its members to the 0-abstraction
level (original attribute values). In Figure 1 the descriptor Any contains two concepts Light and Dark. Since both of
these descriptors have identical ascending membership degrees, presented in the links of the hierarchy, we would
intuitively conclude that they both characterize their direct generalizer equally, therefore |
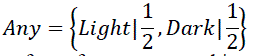 |
Derivation of the descending memberships from fuzzy concept hierarchies has a traightforward character. Each
concept cki in the fuzzy hierarchy can be explained by a set of its direct specializers (i.e. a subset of 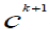 The
membership values are then normalized to allow consistent representation for the fuzzy abstract class cki . So now we
can provide the explanation for each abstract class as follows: The
membership values are then normalized to allow consistent representation for the fuzzy abstract class cki . So now we
can provide the explanation for each abstract class as follows: |
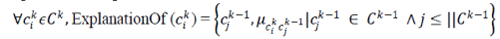 (2) (2) |
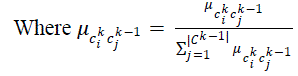 (3) (3) |
| and h ≥ K > 0 , where h is the height of the fuzzy concept hierarchy. |
| In other words, we explain each abstract concept by providing the set of its direct specializes, and the degrees of
their ―descending memberships‖, reflecting the knowledge -based participation (contribution) of these terms in the final
abstract’s construction. |
| Drilling down further in Figure 1, based on the distribution of bottom-up membership values in the hierarchy links,
we can explain Light as {Whitish(2/3), Grayish(1/3)} and consequently Dark as {Grayish(1/3), Blackish(2/3)}. We can
then provide the user with a more detailed definition of the abstract concept any, which is |
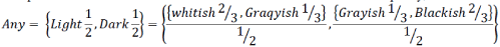 |
| To make To make this explanation clearer we can merge overlapping components. To preserve completeness of the
derived definition we applied the sum operator over the algebraic product when merging all overlapping concepts |
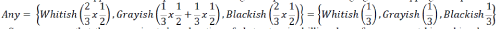 |
So we can see that the approximated explanation of abstracts, via drilling down fuzzy concept hierarchies, has a
transitive character. If we explain, concept 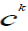 with the subset of with the subset of 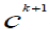 , and then each of the elements from this set with
the concepts from the set CK-2 , then , and then each of the elements from this set with
the concepts from the set CK-2 , then 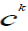 can be also fully explained by the merger of definitions based on the set CK-2. can be also fully explained by the merger of definitions based on the set CK-2. |
| This approach to explanation of abstract concepts has a rather trivial character when none of the abstract’s
components (direct specializes) managed to reach a count of the votes greater than the given generalization threshold
(denoted further as T) and so was reported as a separate entity in the generalized relation. However, in the other case,
we have to make certain that the concepts that reached a significant count at the lower level of abstraction (and were
already placed in the final generalized relation) do not occur in descriptions of higher-level concepts. Otherwise the
explanations would have a confusing character, since the client could be under impression that the same tuples are
reported (and counted) multiple times at different levels of abstraction. We have to remember that final users of data
mining applications are decisions makers who, in contrasts to experts and data analysts, usually do not have time to
gather detailed knowledge about techniques which were applied to generalize the data. Therefore the last equation
should include the restriction: |
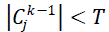 |
where T is the threshold value representing the minimal value of COUNT which is recognized by the client as
significant aggregation of original data (e.g. one may wish all generalized tuples which describe more than T = 5% of the original dataset to be reported separately in the output relation); and 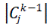 c represents the total number of original
data records generalized to the abstract concept ckj c represents the total number of original
data records generalized to the abstract concept ckj |
| This property assures that each lower-level concept, employed in derivation of a hierarchical explanation, was not
separately reported in the final generalized relation |
EXTRACTION OF MULTI LEVEL ASSOCIATION RULES FROM TOXIC RELEASE INVENTORY DATA |
| A data-mining task, for which we have chosen to empirically test the AOFI method, was to provide a concise and
exact summary of toluene emission in the air of Louisiana in 2001 (the most current dataset provided by U.S.
Environmental Protection Agency). We have chosen this particular toxin since it is a chemical most commonly
reported to the Toxics Release Inventory [13] by the local industrial facilities. |
| Toxics Release Inventory (TRI) is a major EPA database, which has been created under the Emergency Planning and
Community Right-t o-Know Act (EPCRA) in 1986. The 2001 TRI dataset contains information on releases of
approximately 650 toxic chemicals. The data was gathered from over 21,000 manufacturing facilities located within the
US. |
| When performing our method over the dataset we concentrate our analysis on three main aspects: (1) Localization of
the toluene emitters (i.e. discovery of regions in Louisiana which have high air emission of the chemical), (2) Amount
of the toluene air emission in the state (i.e. estimation of the toxicity level in different regions of Louisiana), (3)
Industrial sectors which are responsible for the local toxification (i.e. types of businesses which are emitting toluene in
the air of Louisiana), represented by the federal SIC (i.e. Standard Industry Code) classification. |
| The number of abstract descriptors at each level of concept hierarchies for the analyzed TRI dataset is presented in
Table 1. The second row of this table reflects Pre-Generalization [1], where attribute values are transformed to the
concepts placed at the leaves of the concept hierarchies. Since this phase is performed without an increase of
abstraction level (denoted as 0- abstraction level in Table 1), the descriptors placed in the leaves of the concept
hierarchies are actually the original attribute values. |
| As with regular AOI, we are able to extract separate generalization paths for each attribute value from the concept
hierarchies. However the fuzzy generalization paths can not be implemented in the form of lists but need to be
represented in the form of trees. |
| As in the crisp approach, we are allowed to order steps of generalization according to our preferences. Each stage of
AOI can be characterized by a vector representing the current abstraction level for each of the generalized attributes,
where the order of its elements reflects the order of attributes in the generalized relation. In our example, since we
generalize three columns of the table including task relevant data, we can describe Pre-Generalization as (0, 0, 0),
which reflects the case where all three attributes are at the 0-abstraction level. So the final possible stage (all attribute
values in each column are characterized by a single, most general concept) is a vector (4, 4, 3), which indicates that
attributes FACILITY_LOCALIZATION and SIC_CODE are generalized to the 4th level of abstraction, and the last
attribute, i.e. TOTAL_AIR_EMISSION, is abstracted to the 3rd level (all these levels ar e final, since they reflect roots
of the utilized concept hierarchies). |
| The final, generalized relation, which provides the user with information about only significant clusters of data at the
abstract level, is presented in the Table 2. Each of the generated tuples can be interpreted as a conjunctive rule,
characterizing release of toluene in Louisiana (i.e. the tuples stored in the initial relation). Obviously, the order of AOFI steps could reflect different data mining goals. Since we were particularly interested in analyzing what types of
facilities release toluene into the air in Louisiana we decided to generalize the SIC codes as late as possible. |
| When mapping generated abstract tuples into characteristic rules at a common level of abstraction with quantitative
information about support of these characteristics, we must ensure preservation of the distribution of COUNT
according to the background knowledge as reflected in the fuzzy concept hierarchies. |
| For instance, if we are particularly interested in the business sector classified by government as 51—(i.e. Wholesale
Trade of the Non-durable Goods), we can merge the 1st, 2nd and 11th record of the generalized relation to build the
following characteristic rule: |
| (South ∨ Cajun Country∨ Crossroads) ∧ (51-- ∨ 5169 ∨ 5171) ∧ (Low ∨ Below and about 603). |
| This rule can be further simplified to the form: (South ∨ Crossroads) ∧ 51-- ∧ Low and fit to the abstract description
of 18.99% (i.e.4.52%+4.45%+10.02%) of the originally stored records. However if we want to transform this
characterization to a more general form, such as: South ∧ 51-- ∧ Low , we have to remember that according to the
fuzzy concept hierarchy presented in the Figure 2 only 25% of the Crossroads country lies in the southern Louisiana,
therefore in this generalization a summarization of the COUNT values needs to be appropriately modified: |
| 10.02% + 4.52% + 0.25*4.45% = 15.65%. |
| Now we can conclude that almost 19% of facilities, which officially reported a release of toluene into the air of
Louisiana, are the wholesale traders of nondurable goods and that over 82% of them (i.e. 15.65 / 18.99 = 0.8241) are
located in the Southern part of the state. All these ―51-type‖ facilities released only low amounts of toluene. |
CONCLUSIONS |
| In this paper we first introduced a consistent model of fuzzy induction and then applied it to mine generalized
association rules from environmental data. In addition, we presented how the generated results can be explained to
users via extraction of their approximate definitions. |
| There are many aspects by which we may judge the technique presented here. The ordinary (crisp) AOI will usually
perform with higher computational efficiency then AOFI. However utilization of fuzzy concept hierarchies provides
more flexibility in reflecting expert knowledge and so allows better modeling of real-life dependencies among attribute
values, which will lead to more satisfactory overall results for the induction process. The drawback of the computational cost may additionally decline when we notice that, in contrast to many other data mining algorithms,
hierarchical induction algorithms need to run only once through the original (i.e. massive) dataset. We are continuing
an investigation of computational costs of our approach for large datasets. |
| |
Tables at a glance |
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance |
 |
| Figure 1 |
|
| |
References |
- J. Han , M. Kamber, “Data Mining: Concepts and Techniques”, Morgan Kaufmann, New York, NY, 2000.
- J. Han, Y. Cai, and N. Cercone, “Knowledge discovery in databases: An attribute-oriented approach”, Proc. 18th Int. Conf. Ver y LargeData Bases, Vancouver, Canada, 1992, pp. 547-559.
- J. Han, “Towards Efficient Induction Mechanisms in Database Systems”, Theoretical Computing Science, 133, 1994, pp. 361-385.
- J. Han, Y. Fu, “Discovery of Multiple-Level Association Rules from Large Databases ”, IEEE Trans. on KDE, 11(5), 1999, pp. 798-804.
- C.L. Carter, H.J. Hamilton, “Efficient Attribute- Oriented Generalization for Knowledge Discovery from Large Databases”, IEEE Trans.on KDE, 10(2), 1998, pp. 193-208.
- R.J. Hilderman, H.J. Hamilton, and N. Cercone, “Data mining in large databases using domain generalization graphs”, Journal ofIntelligent Information Systems, 13(3), 1999, pp. 195-234.
- C.-C. Hsu, “Extending attribute-oriented induction algorithm for major values and numeric values”, Expert Systems with Applications,27, 2004, pp. 187-202.
- D.H. Lee, M.H. Kim, “Database summarization using fuzzy ISA hierarchies”, IEEE Trans .on SMC - part B, 27(1), 1997, pp. 68 -78.
- K.-M. Lee, “Mining generalized fuzzy quantitative association rules with fuzzy generalization hierarchies”, 20th NAFIPS Int'l Conf.,Vancouver, Canada, 2001, pp. 2977-2982.
- J. C. Cubero, J.M. Medina, O. Pons & M.A. Vila, “Data Summarization in Relational Databases through Fuzzy Dependencies”,Information Sciences, 121(3-4), 1999, pp. 233-270.
- G. Raschia, N. Mouaddib, “SAINTETIQ:a fuzzy set-based approach to database summarization”, Fuzzy Sets and Systems, 129(2), 2002,pp. 137- 162.
- R. Angryk, F. Petry, “Consistent fuzzy concept hierarchies for attribute generalization,” Proceeding of the IASTED Int. Conf. OnInformation and Knowledge Sharing, Scottsdale, AZ, USA, November 2003, pp. 158-163.
- Toxics Release Inventory (TRI) is a publicly available EPA database hosted at: http://www.epa.gov/tri/tridata/tri01/index.htm
|