Hussein Ahmed Ayed Rababa*
Department of Mathematics, The Hashemite University, Irbid, Jordan
Received: 03-Aug-2022, Manuscript No. JSMS-22-71157; Editor assigned: 08-Aug-2022, Pre QC No. JSMS-22-71157 (PQ); Reviewed: 22-Aug-2022, QC No. JSMS-22- 71157; Revised: 29-Aug-2022, Manuscript No.JSMS-22-71157 (A); Published: 06-Sep-2022, DOI: 10.4172/J Stats Math Sci.8.6.003.
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In this article, the researcher presents a rule for analyzing the sum of two squares, where the researcher studied the different methods of analysis for expressions and algebraic expressions that can be analyzed in different ways. With the Pythagorean theorem, the researcher presented a set of examples that support the validity of the rule to be this. Theorems related to the expression of integers as sums of squares of other integers are known as sum of squares theorems in additive number theory.
Integer norms, Sum of two squares, Statistics, Pythagorean primes
We need a lot to simplify terms and algebraic expressions to facilitate their expression and use in multiple forms and to build parallels that help in proof and proof.
Mathematics and the components it contain, some of which have been created by mathematicians as equal, while others are still under research and study, considering that mathematics is an old and new science that is constantly evolving, spending every moment to search for what is new and proven in order to obtain an integrated science that benefits from the various applied sciences.
After researching and exploring the rule of the sum of two squares, which the current article presents with a new and proven argument, which is a qualitative leap in building the mathematical world, which we strive to provide new additions to what scientists and researchers were unable to provide in the past. The sum of squares function is an arithmetic component used in number theory that calculates the number of representations for a given positive integer n as the sum of k squares. Representations that differ only in the summand order or in the signs of the squared figures are counted as different (n), and is denoted by rk (n).
In statistics, the sum of squares formula is used to measure how accurately a model represents the original information. It displays the dataset's dispersion. The sum of squares formula is used to calculate the sum of two or more squares in an equation. The sum of two or more squares in an expression is calculated using the sum of squares formula. The sum of squares formula is used to indicate how effectively a model represents the data being simulated. The departure from the mean value of the data is also measured using the sum of squares. As a result, it is determined by subtracting the mean from the total sum of the squares.
There are two formulae that may be used to determine the sum of squares: Algebra and the mean. The following is the formula to calculating the sum of the squares of two numbers:
Sum of squares formulas
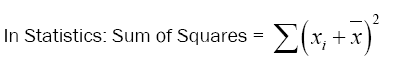
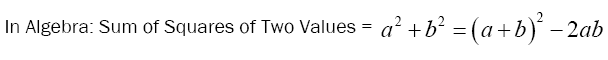
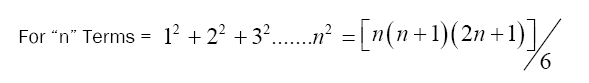
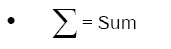
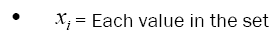
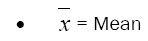
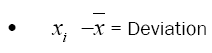
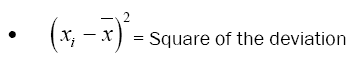
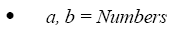
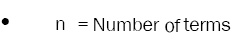
The integer sequences consist of the integers that may be written as the sum of two squares. They constitute a set of all Gaussian integer norms, and their square roots take up the set of all line segment lengths in the twodimensional integer lattice.
With a limiting constant of proportionality, the number of representable numbers in the range from 0 to any integer 
A statistical measure of deviation from the mean is the sum of squares. Variation is another term for it. The squared differences of each data point are combined together to compute it. The sum of squares is calculated by squaring the separation between each data point and the line of best fit, then combining the results.
Preliminaries
Simplifying and analyzing algebraic expressions occupied the minds of mathematicians because of its Mathematics is very important in all the different aspects of life that need mathematics, even in the field of language.
Mathematics involves the study of many subjects such as arithmetic and numbers, algebraic formulas and structures, geometry, and quantities and their changes (calculus and analysis). There is no explicit agreement on its precise and consistent scope or knowledge [1].
Mathematics is extremely important in the natural sciences, computer science, engineering, economics, medicine, social sciences. Statistics and game and logic.
Mathematics has played an important and distinct role in human life since ancient times and was accompanied by written records accompanying human activities. The concept of mathematical proof appeared for the first time among the Greeks, especially in the world of mathematical geometry, Euclid. Mathematics continued to develop slowly and slowly until the Renaissance came, during which the science of algebra and calculus was added to the science of arithmetic and geometry, to be the main base and the basic nucleus in mathematics, which led to the active interaction between mathematical discoveries and scientific innovations, which in turn led to the tremendous development in mathematics , At the end of the nineteenth century, mathematics has invaded all aspects of the various applied sciences, and its multiple applications appear in our daily lives [2].
The term sum of squares refers to the sum of the specified integers squares. It is the sum of the squares of a dataset's variation in statistics. The steps listed below can be used to determine the total sum of squares in statistics:
Step 1: Count the number of data points in the dataset.
Step 2: Calculate the data's mean.
Step 3: Deduct each data point from the mean.
Step 4: Find the square of the difference found in step 3.
Step 5: Add the squares that defined in step 4.
The value provides information about a dataset's degree of dispersion. It provides in a better comprehension of the information by measuring the amount that the data points differ from the mean. A substantial deviation of the data points from the mean value is indicated by a large value for the sum of squares. On the other hand, if the value is small, it indicates that the data's deviation from the mean is not particularly significant.
Most mathematical activities consist of discoveries that have been reached through studies and research that have been proven through thinking, deduction and analysis, The majority of mathematical activities consist of discoveries that are proven through research and thinking, and these discoveries are either abstract natural states such as natural numbers or abstract states such as axioms, and pre-established theories [3].
Diffintion1: A square of a number is the product obtained when the number is multiplied by itself. Square numbers are those numbers whose square root is an integer. If n is a number, then its square is obtained by multiplying n by itself i.e., n x n. The square of a number n is represented as n2 and is read as n squared. Sum of the squares is obtained by adding the squares of the numbers [4].
According to the Pythagorean theorem, the area of the square formed on the hypotenuse is equal to the area of the square formed on the other two sides.
Theorem: 1- Fermat's theorem on sums of two squares
Fermat's theorem for sums the two squares that an odd prime d can be expressed as the formula:
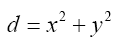
Such that x and y integers numbers, if and only if d =1 (mod 4)
The prime numbers for which this formula is true are called Pythagorean primes.
Euler succeeded proving Fermat's theorem on sums of two squares in 1749. The proof depend on infinite descent [5].
In algebra the sum of two square c2+d2 =(c+d)2 -2cd, And the right-hand side of the equation can be factored as a difference of squares, if 2cd is a perfect square. So the analysis becomes,
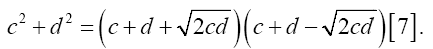
Theorem: 2- A Gaussian prime theorem
A Gaussian integer is a complex number when a +ib are integers. The norm 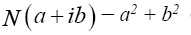 of a Gaussian integer is an integer equal to the square of the absolute value of the Gaussian integer. The norm of a product of Gaussian integers is the product of their norm. This is Diophantus identity, which results immediately from the similar property of the absolute value.
of a Gaussian integer is an integer equal to the square of the absolute value of the Gaussian integer. The norm of a product of Gaussian integers is the product of their norm. This is Diophantus identity, which results immediately from the similar property of the absolute value.
The product of two numbers, each of which is a sum of two squares, is itself a sum of two squares.
This is a well-known property, based on the identity.
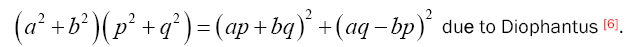
As we can see in the Figure 1, and According to the Pythagorean Theorem, the area of the square formed on the hypotenuse is equal to the area of the square formed on the other two sides [7].
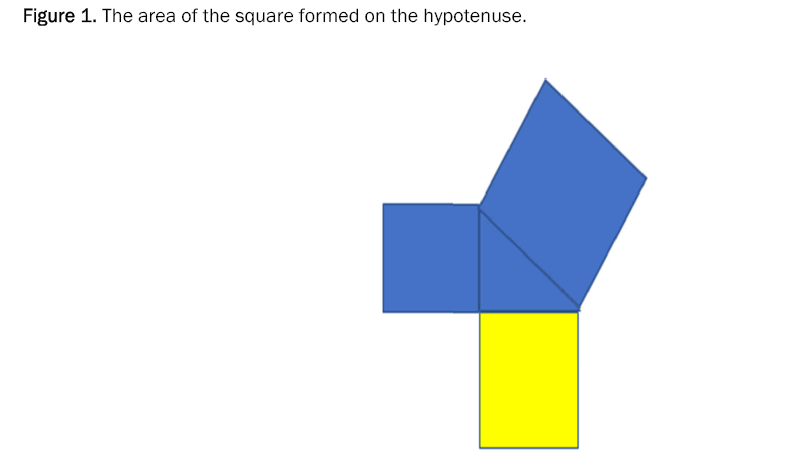
Figure 1: The area of the square formed on the hypotenuse.
The two squares are formed on the two sides of the list and joined in one space to appear to us as Figure 2 ,We take the two squares built on both sides of the right angle and through them we notice.
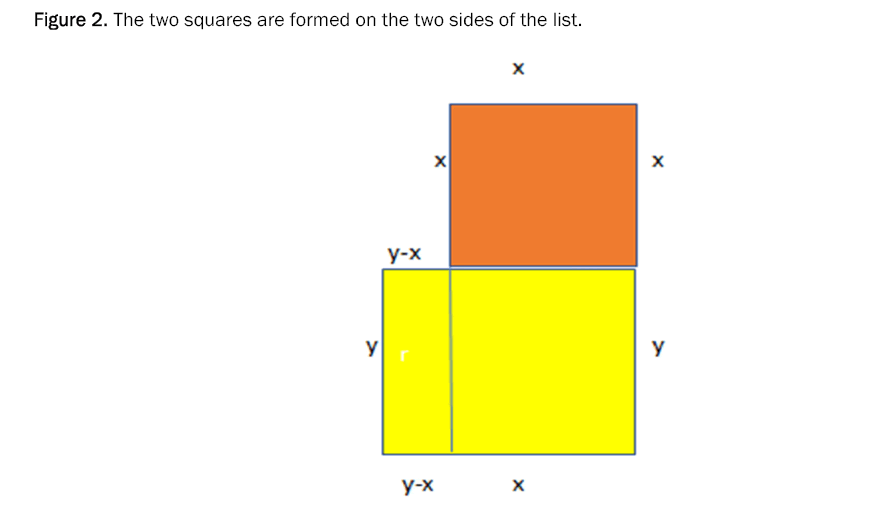
Figure 2: The two squares are formed on the two sides of the list.
And to proof the relationship
We take the two squares built on both sides of the list and through them we notice from Figure 3, The area has become the result of the area of the large rectangle consisting of the rectangle whose dimensions are
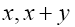
and
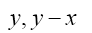
Figure 3: The area of the shape equal x(x+y)+ y(y-x).
So that the area of the two squares is equal to the area of the two rectangles, i.e.
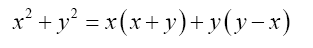
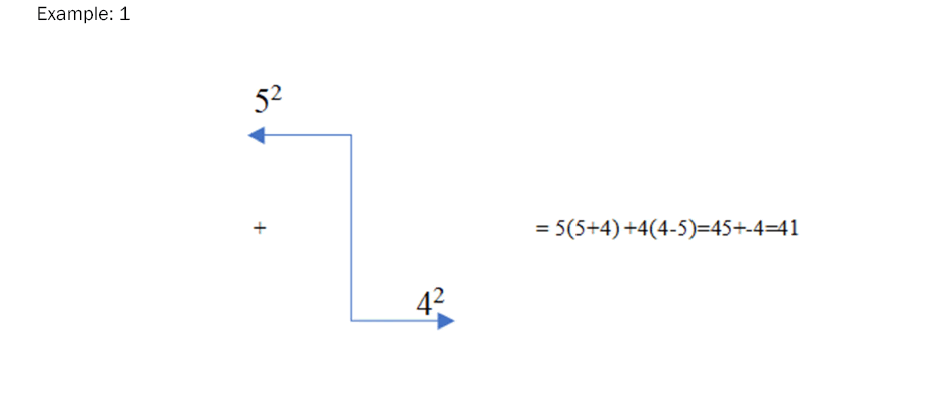
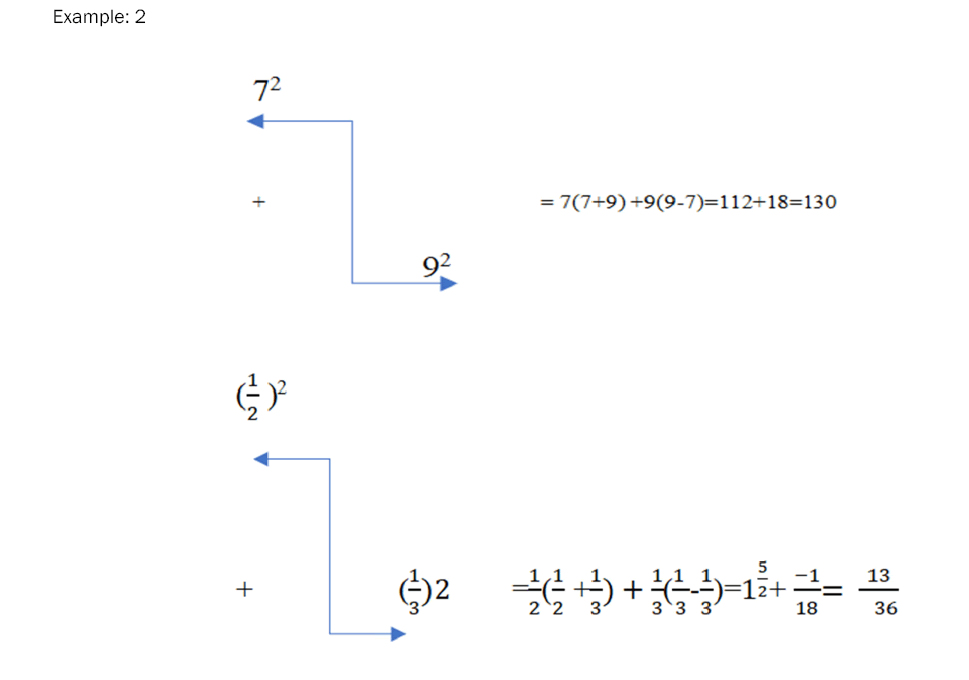
Example
These examples show the validity of the rule in this article for the sum of two squares that the researcher discovered [8].
The new form presented by the current article helps students, scholars and researchers in the field of mathematics to use it for ease of application. It also provides equivalent methods that help in methods of analysis, proof and building teaching strategies that are distinguished by raising students’ motivation to learn, and this in turn helps to adopt teaching methods based on evidence-net through the forms that are more widely to realize. Learners will understand the use of idioms and abstract images. Which opens the way for researchers and those interested in the educational field to think by using the proofs based on shapes and integrating them with teaching methods to be more familiar and closer to the students’ minds.
Author contributions
The author read and approved the last version of the manuscript.
Conflicts of interest
The author declares no conflict of interest.
[Crossref]