International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Discrete Fourier Transform: Approach To Signal Processing

Anant G. Kulkarni1, Dr. M. F. Qureshi2, Dr. Manoj Jha3
  1. Research scholar, Department of Electronics Engineering, Dr. C. V. Raman University, Bilaspur, India
  2. Principal, Professor, Department of Electrical Engineering, Government Polytechnic, Kanker-Narayanpur, Buster, India
  3. Head, Department of Mathematics, Rungta Engineering College, Raipur, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

There are three different way to calculate DFT. First method is using formula of DFT or simultaneous equation. Second is Correlation technique and third one is using Fast Fourier Transform (FFT). First method is useful for understanding of basic idea of DFT, but it is not fit for practical and application purpose. In second method is based on detecting known waveform in another signal. It is used for some specified application. This method is used, when DFT has less than about 32 points. Third method is genius method, where FFT algorithm decomposes a DFT with N points, into N DFTs each with single point It is faster than DFT. These all three methods produce an identical output. Here we focused on FFT. This paper described about of DFT using FFT and its MATLAB implementation. The FFT spectrums for the outputs are analysed.

Keywords
FFT, DFT, Twiddle factor, MATLAB, Window

INTRODUCTION
The Discrete Fourier Transform (DFT), exponential function or periodic signal converted into sin and cosine functions or A - jB form. The discrete signal x (n) (where n is time domain index for discrete signal) of length N is converted into discrete frequency domain signal of length N, where k (where k is frequency domain index for discrete signal) varies from 0 to N - 1. The relation between input samples with sine and cosine the complex DFT output signal is given by:
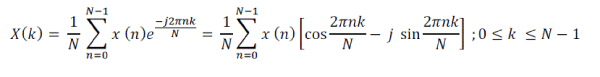image
Figure 01 is DFT tool which convert time domain sampled data into frequency domain sampled data and vice versa. Application of DFT is in field of digital spectral analysis is Spectrum Analysers, Speech Processing, Imaging and Pattern Recognition. Actually FFT is algorithm, which implement DFT. L. G. Johnson (1992) presented Conflict free memory addressing for dedicated FFT hard ware. For high speed single chip implementation, multibank memory address assignment for an arbitrary fixed radix fast Fourier transform (FFT) algorithm is developed. The memory assignment and bank is used to minimize memory size and allow simultaneous access to all the data needed for calculation of each of the radix. Address generation for table lookup of twiddle factors is also included to have small size and high speed. He and Torkelson (1998) proposed a Fast Fourier Transform - Algorithms and Applications presents an introduction to the principles of the fast Fourier transform (FFT). It covers FFTs, frequency domain filtering, and applications to video and audio signal processing. It also has adopted modern approaches like MATLAB examples and projects for better understanding of diverse FFTs. Fast Fourier Transform - Algorithms and Applications is designed for senior undergraduate and graduate students, faculty, engineers, and scientists in the field, and selflearners to understand FFTs and directly apply them to their fields, efficiently. It provides a good reference for any engineer planning to work in this field, either in basic implementation or in research and development. Application of DFT is in field of Filter Design calculating Impulse Response from Frequency Response and calculating Frequency Response from Impulse Response
image

THE FAST FOURIER TRANSFORM (FFT) IS SIMPLY AN ALGORITHM FOR EFFICIENTLY CALCULATING THE DFT
In MATLAB DFT is easily determine using dft command, so that DFT of sequence x (n) = {0, 1, 2, 3} (where N = 4) is,
>> x = [0 1 2 3];
>> dft = fft(x); % The DFT
>> figure(1),stem([0 1 2 3],real(dft))
>> figure(2),stem([0 1 2 3],imag(dft))
>> ifft(dft)
>> x = [0 1 2 3]
x = 0 1 2 3
>> dft = fft(x)
dft = 6.0000 -2.0000 + 2.0000i -2.0000 -2.0000 - 2.0000i
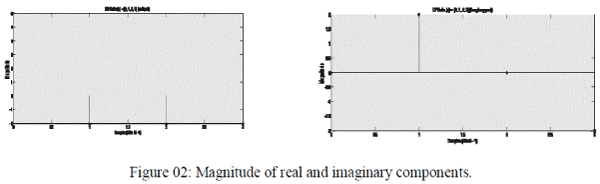
Figure 02 shows the result of output of DFT in magnitude of real and imaginary signal.
image
For development of the FFT twiddle factor WN play important role, this is given by,
This leads to the definition of the twiddle factors as 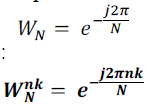image
The twiddle factors are simply the sine and cosine basis functions written in polar form. Note that the 8-point DFT sixty four complex multiplications. In general, an N-point DFT requires N2 complex multiplications. The number of multiplications required is significant because the multiplication function requires a relatively large amount of DSP processing time. In fact, the total time required to compute the DFT is directly proportional to the number of multiplications plus the required amount of overhead.
There are three methods for determining DFT (John G. Proakis et al, 2006). First is analytical method (using formula).
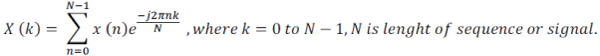image
Second is, by using twiddle factor in formula. Then formula is given by
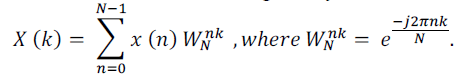image
and third method is matrix method, which formula is shown below,

Methods
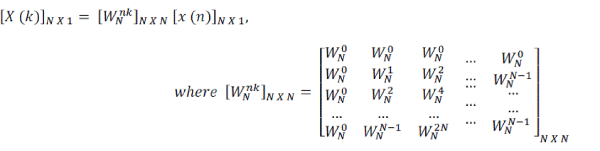image
Similarly for IDFT, this is given by (John G. Proakis et al, 2006)
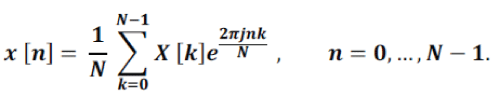image
Negative and zero indices not used in MATLAB DFT, because the starting point index in MATLAB is 1. In the area of spectral analysis, medical imaging, filter bank, telecommunications, data compression are application of DFT.
and matrix formula for IDFT
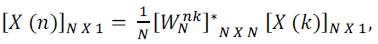DFT is operates on sampled periodic time domain signal. The signal must be periodic in order to be decomposed into the summation of sinusoids. Finite numbers of samples (N) are available for inputting into the DFT. This dilemma is overcome by placing an infinite number of groups of the same N samples “end-to-end,” thereby forcing mathematical (but not real-world) periodicity. Equation for N-point DFT is given by:
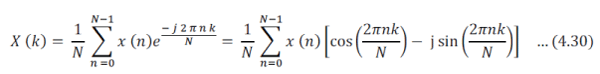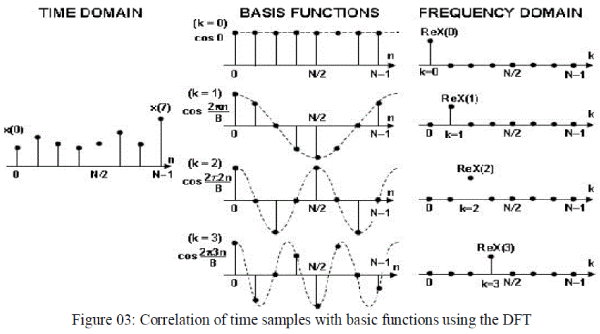
Here X (k) is frequency domain signal, where k is frequency domain index for discrete signal. N is total length of discrete sequence. X (n) is discrete time domain signal, where n is time domain index for discrete signal. Value of k and n are from 0 to N – 1. The DFT output spectrum, X(k), is the correlation between the input time samples and N cosine and N sine waves. Figure 03 shows the concept of correlation. In this figure, the real part of the first four output frequency points is calculated, therefore, only the cosine waves are shown. A similar procedure is used with sine waves in order to calculate the imaginary part of the output spectrum. The first point, X (0), is simply the sum of the input time samples, because cos (0) = 1. The scaling factor, 1/N, is not shown, but must be present in the final result. X (0) is the average value of the time samples, or simply the DC offset. The second point, Re X(1), is obtained by multiplying each time sample by each corresponding point on a cosine wave which makes one complete cycle in the interval N and summing the results. The third point, Re X(2), is obtained by multiplying each time sample by each corresponding point of a cosine wave which has two complete cycles in the interval N and then summing the results. Similarly, the fourth point, Re X(3), is obtained by multiplying each time sample by the corresponding point of a cosine wave which has three complete cycles in the interval N and summing the results. This process continues until all N outputs have been computed. A similar procedure is followed using sine waves in order to calculate the imaginary part of the frequency spectrum. The cosine and sine waves are referred to as basic functions. Correlation of time samples with basic functions using the DFT for N = 8 are shown below:
image

THE FAST FOURIER TRANSFORM (FFT) VS. THE DISCRETE FOURIER TRANSFORM (DFT)
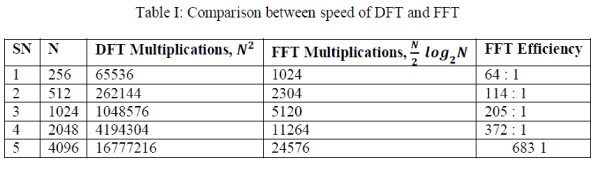
For N = 1024 points DFT computations DFT takes 1,048.576 computation and for FFT it takes 10, 240 computations. The FFT is over 100 times faster. However, the number of computations given is for calculating 1024 harmonics from 1024 samples. The computational efficiency of the FFT versus the DFT becomes highly significant when the FFT point size increases to several thousand as shown in Table I.
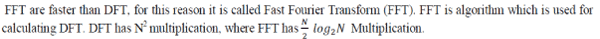image
image

FREQUENCY RESPONSE OF RECTANGULAR, HAMMING, AND BLACKMAN WINDOWS FOR N = 256
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. Applications of window functions are spectral analysis, filter design and non-negative smooth "bell-shaped" curves. For spectral analysis, functions cos ωt is zero, except at frequency ±ω is the output of Fourier transform. However, many other functions and waveforms do not have convenient closed form transforms.
In either case, the Fourier transform can be applied on one or more finite intervals of the waveform. In general, the transform is applied to the product of the waveform and a window function. Any window affects the spectral estimate computed by this method. FFT windows reduce the effects of leakage and only change the shape of the leakage. The signal is measured during a finite measurement time or 'window'. The infinite duration impulse response can be converted to a finite duration impulse response by truncating the infinite series at n = ±N. But, this result in undesirable oscillations in pass band and stop band of the digital filter. This is due to the slow convergence of the Fourier series near the point of discontinuity. These undesirable oscillations can be reduced by using a set of time-limited weighting functions, w (n), called as window functions, to modify the Fourier coefficients.
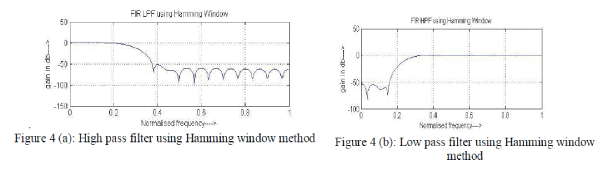
There are various window functions like Rectangular, Hamming, Hanning, Blackman and Kaiser Window function, which converted discontinuities in H (ejω) into transition bands between values on either side of the discontinuity. Here we take simple example of window i. e. Hamming window.
In figure 4 (a) shows Hamming window. These represent the frequency response of Hamming window for high pass filter and figure 4 (b) represents the same for low pass filter. It has moderate transmission width of main lobe as compare to rectangular and Blackman window. Minimum stop band attenuation is approximately -53 dB and the peak of first lobe is approximately -43 dB.
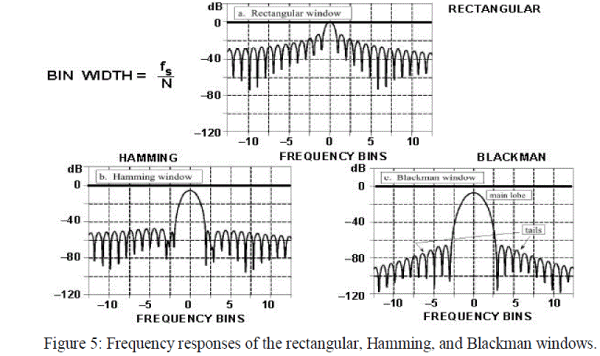
image
Leakage presents in frequency domain due to discontinuities at the endpoints of the data window and because of the harmonics are generated. In addition to the side lobes, the main lobe of the sine wave is coated over several frequency bins. This process is similar to multiplying the input sine wave by a rectangular window pulse which has the familiar [sin(x) / x] frequency response and associated smearing and side lobes. Window function data points are usually precalculated. Window function data points stored in the DSP memory to minimize their impact on FFT processing time. The frequency response of the rectangular, Hamming, and Blackman windows is shown in Figure 5.
image

FAST FOURIER TRANSFORM AND MATLAB IMPLEMENTATION
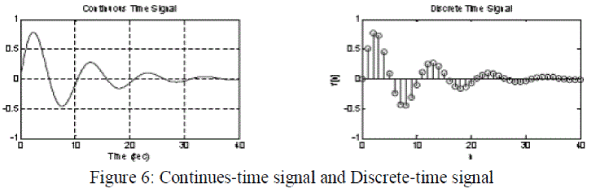
Signal is one dimensional, two dimensional or multidimensional physical variables, which vary according to time, space or any independent variables. There are two main categories of signal. First is continuous time signal and second is discrete time signal. Main source of the signal is continuous time signal. With the help of sampling we can convert continuous time signal into discrete time signal. In discrete time signal, time is in discrete form and magnitude is in continuous format. Figure 6 shows continuous and discrete time signal. Next extension digital signal is completely discrete signal; time and magnitude both are in discrete form.
image
Similarly periodic and non-periodic are two types of signals. Periodic signal consist fundamental period T, Which is minimum interval on which a signal repeats. Period T is reciprocal of f (T = 1/f). Harmonic frequency is kf or kf0.
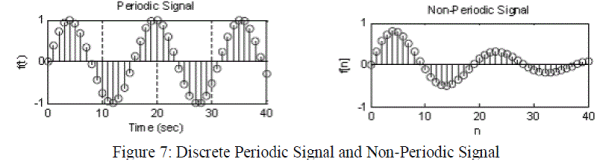image
Any periodic signal can be approximated by a sum of many sinusoids at harmonic frequencies of the signal (kf0) with appropriate amplitude and phase. Sinusoidal signal consist complex exponential function which having positive and negative harmonic frequencies. Euler formula shows
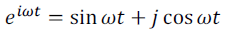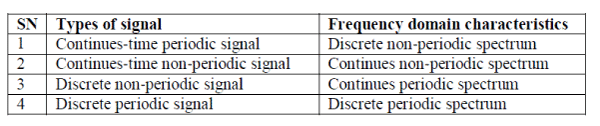
image
Using Fourier analysis, table shows the time domain signal and frequency domain signal relation:
image
Last two transformations are very useful because discrete is associated with both time‐domain and frequency domain is because computers can only take finite discrete time signals. Using the Fourier series representation we have Discrete Fourier Transform (DFT) for finite length signal. DFT can convert time‐domain discrete signal into frequency domain discrete spectrum. Assume for signal x [n], where n vary from n = 0 to N – 1. Then DFT of the signal is a sequence for
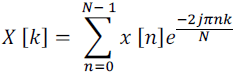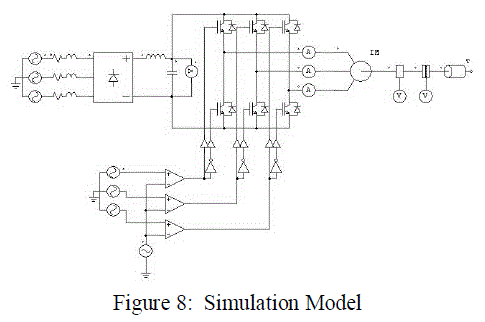
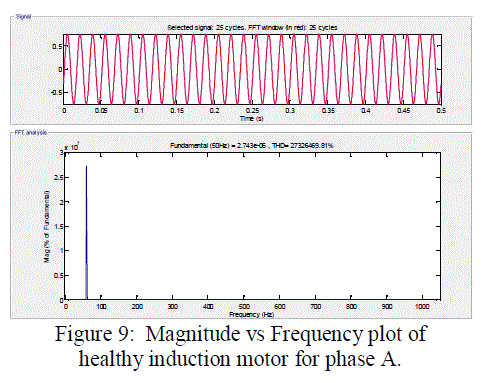
image
Output signal X [k] is frequency domain signal, which is completely discrete in nature due to k. k varies from 0 to N – 1. Motor current, voltage, speed, developed electromagnetic torque along with supply main currents are sensed and analyzed (Namburi N. R. et. al, 1985). Appling FFT analysis obtained motor current in frequency domain. Simulation model is shown in figure 8 and it result is shown in figure 9. Figure 10 shows result for faulty condition.
image
image

CONCLUSION
From simulation result and their FFT analysis in figure 9 and 10, it is cleared that for line to ground fault at one of the motor phase terminals phase A having single spike with small another harmonics as compared to healthy motor. Recent developments have been in the application of Fourier methods to problems which, due to computational effort, would not be tractable were it not for the use of the DFT-FFT method. Presently, some computers with particular purpose are being manufactured for the real-time digital Fourier methods. There are numerous areas in which a greater degree of development in future can be expected. The numerical solution of differential equations, multiple time series analysis, filtering and image processing are some the problems among these.
 

References