In this paper, we study an efficient face recognition technique using combined approaches of discrete cosine transform (DCT) and principal component analysis (PCA). In DCT-PCA, PCA is applied onto the extracted DCT coefficients of the face images. This technique is based on the Fourier spectra of the facial images. The experiments are conducted on the standard face datasets such as ORL, UMIST and real dataset and the performance of the DCT-PCA technique is compared with the existing DCT and PCA. From the experimental results, it is proved that the DCT-PCA based technique for face recognition has improved recognition rate than the conventional PCA and DCT approaches.
Keywords |
| Discrete Cosine Transform, Principal Component Analysis, Face recognition. |
INTRODUCTION |
| Biometric based techniques have gained popularity in recent years. It has become the successful option for identifying
the individuals. Any physiological/behavioral characteristics can be used to identify an individual as long as it is
permanent (invariant) or distinct for each individual [1]. The face recognition techniques have become an active
research area in recent years. Face recognition is a technique to recognize the person face from a still image or
anyvideo. To develop such a system, we use image database of face images [2]. |
| Several approaches for face recognition have been presented in the literature. Dimensionality reduction is essential for
extracting effective features and reducing computational complexity in classification stage. Principal component
analysis (PCA) [3], [4], linear discriminate analysis (LDA) [5] and discrete cosine transform (DCT) [6] are the main
techniques used for data reduction and feature extraction in the appearance based approaches. The PCA based models
operate in vectors. They use Eigenface based approaches. In the literature of pattern recognition, several PCA variants
are in use such as modular PCA [7], Kernel PCA [8], independent component analysis [9] etc. The two dimensional
(2D) PCA eliminates the need of converting 2D image matrices into 1D vector unlike conventional PCA [10]. While
the 2D PCA worked only in one direction, either in row or column, two directional 2D PCA work in both directions
simultaneously [11]. On the other hand, DCT based techniques extracts most significant DCT coefficients of the
training images as a part of feature extraction. Certain normalization techniques can improve the robustness of the DCT
based face recognition system to variations in facial geometry and illumination [12]. The DCT can either be applied to
entire frontal face image to obtain global DCT features or the local features like nose, eyes etc can be extracted
manually and then DCT can be applied onto them to form local DCT features. When local and global features are
combined, DCT gives a relatively high recognition rate [13]. In DCT-PCA based face recognition technique, PCA is
directly applied on the extracted DCT coefficients of the face images, thus achieving dimensionality reduction and also
improved recognition rates [14]. |
| In this paper, we have made an attempt to study the DCT-PCA based technique for face recognition. We also compare
this technique with the conventional PCA and DCT and present a comparative study. The experimentations are
performed on the standard face datasets like ORL, UMIST and a real dataset. The rest of the paper is organized as
follows: PCA is discussed in section 2, DCT and DCT-PCA based face recognitions are discussed in section 3, the
section 4 presents the experimental results. The final work is concluded in section 5. |
PRICIPAL COMPONENT ANALYSIS BASED FACE RECOGNITION |
| The idea of using PCA as feature extraction technique to represent face images was first developed by Kirby and
Sirovich [3]. This approach was later used in face representation and recognition technique by Turk and Pentland [4].
The PCA used Eigenface based technique, where in the 2D image matrices of all the training face images are
transformed into 1D vectors and then represented as a point in the high dimensional vector space, known as Eigen
vector space. |
| Let a1,a2,a3,….,aMbe M training samples each of size r x c. Each 2D image matrix ai (i=1,2,…,M) is converted into 1D
image vector and then mean centered by subtracting the mean image from each vector as follows: |
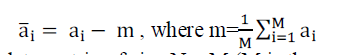 (1) (1) |
| The data matrix of size N x M (M is the number of training images& N=r*c, is the number of elements in ai) is formed
by using the mean centered image vectors as: |
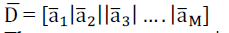 (2) (2) |
Then we compute covariance matrix by multiplying data matrix  and its transpose: and its transpose: |
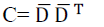 (3) (3) |
The Eigen vectors of the covariance matrix are computed and kEigen vectors corresponding to the klargest Eigen
values are ordered in descending order to form the Eigenface space. Let 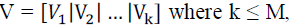 , be obtained
Eigenface space. , be obtained
Eigenface space. |
| Once Eigen space is obtained, each of the centered training image vectors (ai) are projected into the Eigen space. |
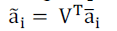 (4) (4) |
| In the classification stage, first test image is mean centered by subtracting the mean image from the test image vector. It
is then projected into the obtained Eigen vector space as: |
 (7)
(7) |
And 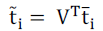 (6) (6) |
| The comparison is done between the projected test image and each of the training images using similarity measure. The
training image found to be closest to the test image is used to classify the test image. The most well known similarity
measure is Euclidean distance. |
DCT AND DCT-PCA BASED APPROACHES |
| The DCT is an invertible linear transform that can express a finite sequence of data points in terms of a sum of cosine
functions oscillating at different frequencies. The original face image is converted to frequency domain by applying 2D
DCT. The original image can be restored back from the DCT coefficients by using invert 2D DCT [6]. |
| In DCT based face recognition, important frequency components of the training image, obtained by DCT function is
extracted. The feature vectors for the training images contain this extracted, more relevant information. In the
classification stage, the feature vectors obtained for the training images and test image are compared using a similarity
measure, mostly Euclidean distance. A training image with minimum distance is used to classify the test image.
Given an r by c image f(r,c), 2D r by c DCT is defined as follows: |

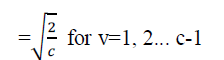
|
| In DCT-PCA based approach, initially the 2D DCT function given in equation (7) is applied on the face images to
obtain the DCT coefficients. Among these coefficients, we extract only those coefficients that represent more relevant
information. Once the relevant frequency components are extracted, PCA is then applied onto them for feature
extraction [14]. By applying PCA on the extracted DCT coefficients, higher compression rate is achieved and also
recognition rate can be improved. |
EXPERIMENTAL RESULTS |
| Our experimentation involves use of two standard face datasets ORL and UMIST and a real dataset, which consists of
faces with slight variations in pose, illumination, expressions etc. |
Results on ORL face dataset |
| The ORL dataset consists ofgrayscale face images of 40 persons with 10 samples of each. The images are rescaled to
112 x 92 sizes. They represent slight variations in pose and expressions. The fig.1 shows the sample images of ORL
dataset. |
 |
| The experimentation includes varying the number of training samples in various ways. We have considered first
alternate samples such as (i) 1, 3, 5, 7, 9, (ii) 2, 4, 6, 8, 10 for training and rest of the samples for testing. Then we also
considered for training, the continuous samples (iii) 1, 2, 3, 4, 5, (iv) 6, 7, 8, 9, 10, (v) random 7 and (vi) random 4
samples of all face images for training and remaining for testing. In all the above experiments, we record the
recognition accuracy of the implemented algorithm under different dimensions of feature vector. The different
dimensions considered in our work are 5, 10, 15, 20 and 25. |
| In this paper, we have considered DCT-PCA for implementation and its performance is compared with traditional PCA
and DCT. The experimental results obtained using DCT-PCA on ORL dataset is plotted in the fig 2. In DCT-PCA,
first, we applied 2D DCT function on the training face images; from the DCT coefficients of the face images, 100 most
relevant frequency components are extracted. On these extracted DCT coefficients of the face images, PCA is applied,
which further reduces the dimensionality of the features extracted from the images. In order to perform a comparative
analysis, we have conducted the same set of experiments mentioned above on PCA and DCT. The results obtained by
using PCA on ORL dataset is shown in Fig. 3. |
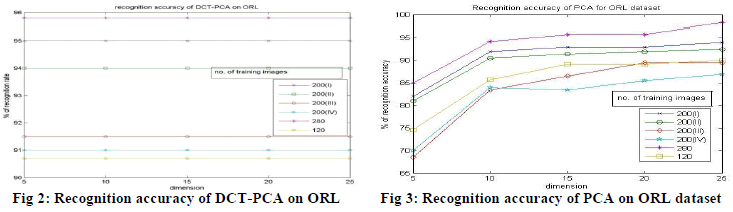 |
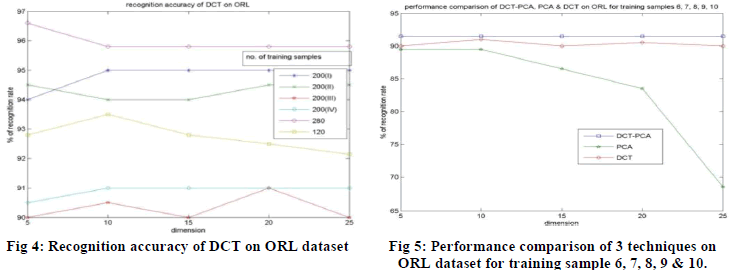
| The performance of DCT technique on ORL dataset is shown in fig. 4. From the experimental results obtained on ORL
dataset, we can say that the performances of DCT and DCT-PCA are better than PCA. Also the DCT-PCA performs
better than DCT in most cases, except when there is small number of training samples. And also, the number of
coefficients for face representation used by DCT-PCA is less compared to DCT. Therefore, we can say that the DCTPCA
outperforms the other two approaches, which is clearly shown in fig. 5 that plots the performances of 3 algorithms
on ORL for the training samples 6, 7, 8, 9 and 10. |
 |
Results on UMIST face dataset |
| Another dataset considered for experimentation in this paper is UMIST dataset. It consists of face images of 20 persons
with varying number of samples of each. For our experiments, we have considered only 15 samples of each person. The
fig.6 shows 15 such samples of a person in UMIST. |
 |
| The same set of experiments that are conducted on ORL, are also performed on UMIST dataset for all the different face
recognition approaches mentioned in this paper. That is, here out of 15 samples of each person, we have considered
subset of samples for training and rest for testing in the similar way as in ORL. The recognition rates obtained using
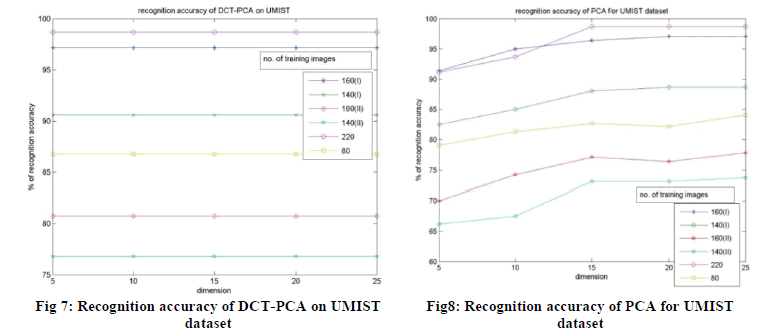
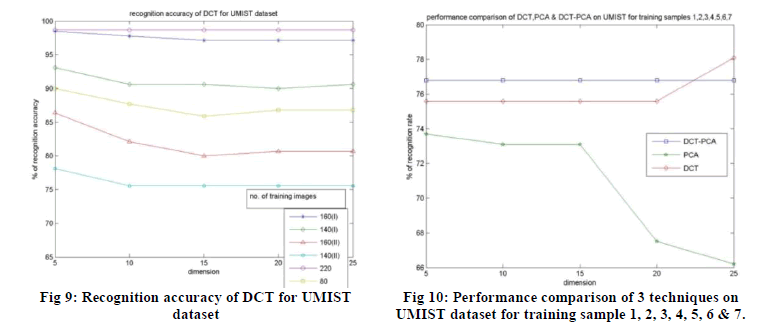
DCT-PCA, PCA and DCT on UMIST are plotted in fig. 7, fig. 8 and fig. 9 respectively. |
| From the experimental results obtained on UMIST dataset, we can analyze that the DCT and DCT-PCA outperforms
the conventional PCA as in the case of ORL dataset. On the other hand, the DCT and DCT-PCA performs almost in the
similar manner on UMIST dataset, in some cases DCT-PCA performs better. Whereas the performance of DCT
improves even when there is decrease in dimension of feature vector. Since the DCT-PCA uses less number of
coefficients for face representation than DCT, we can say that DCT-PCA is an efficient face recognition technique. The
fig. 10 shows a plot of the performances of 3 algorithms on UMIST for the training samples 1, 2, 3, 4, 5, 6 and 7, which
clearly shows that the DCT-PCA performs better. |
 |
 |
Results on real face dataset |
| We also have extended our work on real face dataset, which consists of 16 persons each with 7 face samples. They
represent slight variations in pose, expression and illumination. The 7 such samples of a person in real dataset are
shown in fig. 11. |
 |
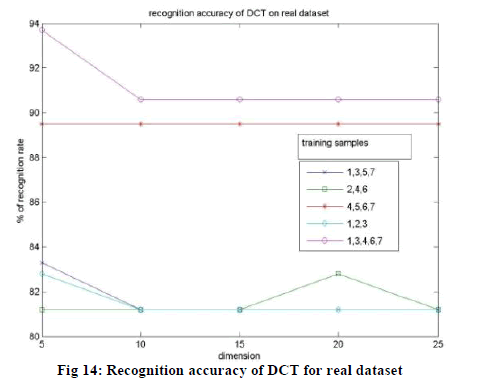
| The experimental results obtained using DCT-PCA, PCA and DCT on real dataset are shown below in the Fig. 12, 13
and 14 respectively. We have kept almost the same experimental set up that are used on ORL and UMIST for real
dataset as well, except thatonly 1 set of random samples (random 5 samples 1,3,4,6,7) is considered for training, unlike
the case of ORL or UMIST. |
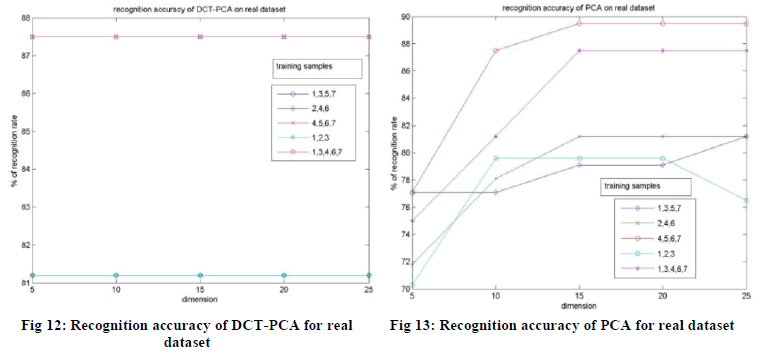 |
| In the case of real dataset, the DCT-PCA doesn’t produce an improved recognition rate than DCT, but gives a better
result than PCA. But we can still say that among three approaches, DCT-PCA is better since it uses very less amount of
coefficients for face representation and achieves higher compression than DCT. As in the case of ORL and UMIST, the
performance of DCT-PCA does not go down with decrease in the dimension of feature vector even in real dataset,
which is an advantage. |
 |
CONCLUSION |
| In this paper, we implemented and tested the three approaches for face recognition, PCA, DCT and an integrated
approach called as DCT-PCA. The experiments are carried out on the standard datasets like ORL and UMIST and a
real dataset. Various experiments are conducted using the three algorithms on these datasets; it included varying the
number of training samples in different possible ways under different dimensions of feature vector. |
| From the experimental results, we conclude that the DCT and DCT-PCA techniques, which works in frequency
domain, gives better recognition accuracy than PCA that work in spatial domain. Also, the DCT-PCA which is a
combination of DCT and PCA, works better than other two techniques in terms of recognition accuracy and
computationally efficiency. |
References |
- Jain et al., “An introduction to biometric recognition”, IEEE transactions on circuits and systems for video technology, vol. 14, no. 1, January 2004.
- Jigar M. Pandya, DevangRathod, Jigna J. Jadav, “A Survey of Face Recognition approach “, International Journal of Engineering Research and Applications (IJERA) ISSN: 2248-9622 Vol. 3, Issue 1,, pp.632-635, January -February 2013.
- M. Kirby and L. Sirovich,“Application of the Karhunen-Lokve procedure for the characterization of human faces”, IEEEtransactions on pattern analysis and machine intelligence. vol. 12.no. 1 . january 1990.
- M. A. Turk and A. P. Pentland, “Eigenfaces for recognition,” J. Cogn.Neurosci., vol. 3, pp. 71–86, 1991.
- C. Zhou, et al., “Face recognition based on PCA image reconstruction and LDA”, Optik - Int. J. Light Electron Opt., http://dx.doi.org/10.1016/j.ijleo.2013.04.108 (2013).
- Prof. AnandNajan, Prof. Mrs. A. C. Phadke, “DCT Based Face Recognition”, International Journal of Engineering Innovation & Research, Volume 1, Issue 5, ISSN : 2277 – 5668.
- RajkiranGottumukkal, VijayanK.Asari, “An improved face recognition technique based on modular PCA approach”, Pattern Recognition Letters25 ,429–436, (2004).
- M.H. Yang, “Kernel Eigenfaces vs. Kernel Fisherfaces: Face Recognition Using Kernel Methods,” Proc. Fifth IEEE Int’l Conf. Automatic Face and Gesture Recognition (RGR’02), pp. 215-220, May 2002.
- M.S. Bartlett, J.R. Movellan, and T.J. Sejnowski, “Face Recognition by Independent Component Analysis,” IEEE Trans. Neural Networks, vol.13, no. 6, pp. 1450-1464, 2002.
- J. Yang, D. Zhang, A.F. Frangi, J.Y. Yang, “Two-dimensional PCA: a new approach to appearance based face representation and recognition”,IEEE Trans. Pattern Anal. Mach. Intell. 26 (1) 131–137, (2004).
- Daoqiang Zhang, Zhi-Hua Zhou,“ (2D2 PCA): Two-directional two-dimensional PCA for efficient face representation and recognition”,Neurocomputing 69, 224–231,(2005).
- Ziad m. Hafed and Martin D. Levine, “Face recognition using the discrete cosine transform”, International Journal of Computer Vision 43(3),167–188, 2001.
- Aman R. Chadha, Pallavi P. Vaidya, M. Mani Roja, “Face Recognition Using Discrete Cosine Transform for Global and Local Features”, Proceedings of the 2011 International Conference on Recent Advancements in Electrical, Electronics and Control Engineering (IConRAEeCE) IEEE Xplore: CFP1153R-ART; ISBN: 978-1-4577-2149-6.
- Swarup K.D, Sukadev Maher, “New Technique forDCT-PCA Based Face Recognition”, InternationalConference on ElectronicSystems,http://hdl.handle.net/2080/1356, 2011.
|