Kuessi Prince Houssou*
Department of Taxation and Finance, International University of Management and Administration, Cotonou, Benin
Received: 24-Jun-2023, Manuscript No. JSS-23-103721; Editor assigned: 26-Jun-2023, Pre QC No. JSS-23-103721 (PQ); Reviewed: 10-Jul-2023, QC No. JSS-23-103721; Revised: 27-Dec-2023, Manuscript No. JSS-23-103721 (R); Published: 04-Jan-2024, DOI:10.4172/JSS.10.1.001
Citation: Houssou KP. Does Corruption Foster Income Inequality in Sub-Saharan African Countries? RRJ Soc Sci. 2024;10:001.
Copyright: © 2024 Houssou KP. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Research & Reviews: Journal of Social Sciences
The aim of this paper is to analyse the effect of corruption on income inequality for Sub-Saharan African (SSA) countries. To do so, the paper uses panel data covering the period 2002-2017, the Fractional Regression Method (FRM) as well as the Generalized Moment Method (GMM-two stage system) to highlight the effect of corruption on income inequality for 44 SSA countries. The results of the estimations show that with the FRM method the Corruption Perception Index (CPI) is statistically significant and positively affects the GINI index which represents the income inequality indicator, and with the GMM method that better governance of states in terms of controlling corruption significantly reduces income inequality.
The main contribution of this research is both academic and political. On the academic side, it fills the gap in the literature on the link between corruption and income inequality, particularly in SSA. On the policy side, the paper suggests that controlling the level of corruption in the public sector by the relevant institutions should be considered one of the most effective weapons in reducing income inequality in SSA countries.
Corruption; Income inequality; Sub-Saharan Africa (SSA); Fractional Regression Method (FRM); Generalized Moment Method (GMM)
The issue of income inequality is one of the greatest global development challenges. Indeed, according to the United Nations Development Programme (UNDP), the income gap between rich and poor is a development problem. In the literature, there are two opposing theories on the economic and social mechanisms that create inequality [1]. The liberal theory, which argues that only market forces, individual initiative and increasing productivity can truly improve incomes and living conditions in the long run, especially for the most disadvantaged. Therefore, public redistributive action, besides being moderate in size, should be limited to tools that interfere as little as possible with the risk of disrupting the 'virtuous mechanism'. In contrast, socialist theorists believe that only social and political struggles can lead to the reduction of the misery of the poorest produced by the capitalist system and that public redistributive action must penetrate the heart of the production process to challenge the way market forces determine the profits appropriated by capital owners as well as the inequalities between employees [2].
For Piketty, if inequalities are due to factors that individuals do not control, such as inequality in initial endowments transmitted by family or good fortune, for which the individuals concerned cannot be held responsible, then it is right that the state should seek to improve the lot of the most disadvantaged, i.e., those who have had to deal with the most unfavourable uncontrollable factors, in the most effective way possible [3].
Corruption can be one of those uncontrollable factors that are most detrimental to the poor. Thus, corruption can be a driver of income inequality. Many studies have been carried out on the particular role corruption plays in income inequality. Stigler's economic theory of regulatory capture suggests that corruption can foster income inequality by allowing political and economic elites to monopolise resources and enrich themselves at the expense of the population. This issue is particularly acute in Sub-Saharan Africa, one of the regions of the world most affected by corruption [4].
Empirically, most researchers agree that there is a very important relationship: corruption can change the composition of social spending to the benefit of the rich and the detriment of the poor, leading to increased inequality. Dusha finds a feedback effect between corruption and income inequality. However, as Charron et al., show in their model, although corruption and inequality are indeed strongly correlated, some European countries (including Bulgaria, Slovenia and Slovakia) have high corruption and low inequality, which casts doubt on the positive relationship between corruption and income inequality in the specific case of post-communist countries [5].
The literature on the effects of corruption on income inequality is therefore still inconclusive. The counter-intuitive idea that corruption can reduce income inequality and increase social welfare challenges the conventional view that corruption has a negative impact on income distribution [6]. The existence of divergent results on the effect of corruption on income inequality therefore calls for more empirical studies on this issue. The main challenge of our work is to contribute to this debate by assessing the effect of corruption on income inequality in SSA countries over the period 2002-2017 using an empirical model. In other words, we attempt to answer the question: does corruption increase the income gap between rich and poor in SSA countries?
The main contribution of this study is that it builds on the work cited above by filling in the gaps in the literature on the link between corruption and income inequality in SSA. Indeed, to our knowledge, very few studies document the effect of corruption on income inequality in the specific case of SSA countries. This study fills this gap for 44 SSA countries. The findings and recommendations can be used to guide policies aimed at reducing income inequality in all countries [7].
The work is structured as follows. First, a synthesis of previous work on the effect of corruption on income inequality is made (section 2). Second, the methodology adopted (theoretical model, empirical model, nature of the definition and source of variables) in this work is described in Section 3. Section 4 presents the results and their discussion. The last section presents the conclusion and policy implications [8].
Corruption and income inequality: A synthesis of the literature and some stylised facts
Summary of the literature: In the empirical literature, the results of analyses of the relationship between corruption and income inequality fall into three categories. Some authors find that corruption increases income inequality. Others find that this increase in income inequality by corruption occurs when corruption is interacted with other variables. Finally, other authors find that it is rather income inequality that affects corruption [9].
The first group of authors shows that countries with higher corruption also have higher income inequality. In societies where the number of corrupt officials, politicians and bosses willing to break the law to enrich themselves grows faster than the number of honest officials, politicians and bosses, income inequality will continue to grow. Similarly, inequality thrives in societies where corruption depends purely on the honesty of citizens. In a society that lacks incentive, regulatory and institutional systems to detect and punish misappropriation of public funds, corruption becomes more and more severe and consequently has a significant impact on income inequality [10]. Wong, through a cross-sectional time series analysis of 127 countries between 1964 and 2007, shows that corruption positively affects income inequality, especially in developing countries. In the same vein, Zandi et al., used balanced panel data from 2006 to 2020 for 12 Asian developing countries collected from transparency international and World Bank (WDI) databases and, a Random Effect Model (REM) and also the Generalized Moment Method (GMM) to examine the relationship between a number of explanatory variables including corruption and an explained variable which is income inequality. The authors' results reveal that corruption positively and significantly influences income inequality. Gupta et al., found that as corruption increases, the economy becomes less egalitarian, with inequality captured by the Gini index. Using the instrumental variable to fix the direction of causality, they found that corruption actually increases income inequality. They found that a one-point increase in corruption leads to a 7.8% per year decrease in income for the poorest. This can be explained by the fact that the benefits of corruption are likely to accrue to the best connected people in the wealthiest groups. The best connected individuals are more likely to get the best public contracts, thus undermining the government's ability to ensure an equitable distribution of resources [11].
Other studies have argued that the positive effect of corruption on income inequality is inverted form U. Li et al., based on their results, found that inequality appears to reduce with further reductions in the level of corruption, but only when the corruption index exceeds 2.91 (a higher corruption index indicates lower levels of corruption). Following this logic, Messy exploits a panel dataset on Sub-Saharan Africa for the period 1996-2017 on a sample of 22 Sub-Saharan African countries to re-examine the effect of corruption on income inequality in Sub-Saharan Africa. Applying a threshold model approach such as Panel Smooth Transition Regression (PSTR), the author's results confirm the non-linear nature of this relationship. He concludes that corruption increases income inequality in Sub-Saharan Africa only if the corruption rate is high. Otherwise, the effect of corruption is not detrimental [12].
In contrast to these authors, a study by Dobson and Ramlogan-Dobson, using panel data for Latin America, finds evidence that contradicts the results of most previous studies. Specifically, they find a negative relationship between corruption and income inequality, i.e. lower levels of corruption lead to higher levels of income inequality. Thus, effective anti-corruption measures may actually increase income inequality. They argue that an appreciable amount of corruption is necessary to keep the system 'balanced' [13].
For the second group of authors, Isoyami et al., analysed the individual and interaction effects of informality and corruption on income inequality in Nigeria over the period 1996-2020 using the distributed autoregressive lag test technique. The results of this study show the existence of a long run relationship between informality, corruption and income inequality [14]. The individual effects of informality and corruption on income inequality are negative and statistically significant in both the short and long run. However, the study shows that reducing corruption in one year was found to reduce income inequality in the following year. Furthermore, the interaction effect of informality and corruption on income inequality was found to be negative and statistically significant in both the short and long run. The authors therefore conclude that reducing corruption proved to be a necessary but not sufficient condition for reducing inequality [15]. For Maqbool and Ali, it is rather the interaction of corruption control and foreign aid that succeeds in reducing income inequality. The authors, through the Generalized Moment Method (GMM) applied to panel data comprising 78 recipient countries for 14 years found a negative and significant result of the interaction of foreign aid and corruption control on income inequality. As for the work of Aktas, the author shows, using annual data from 19 Central and Eastern European (CEE) countries for the period 1999-2019 and following the modelling of Hansen and Wang, that an increase in corruption and abuse of social transfers by public officials can amplify income inequality [16].
The third group of authors argues that there may be an inverse causal relationship between corruption and income inequality. They argue that income inequality could in fact be a driver of corruption, which could be a reaction to a perceived unfair distribution of income. For example, Khan, using balanced panel data for 23 emerging countries from 1996 to 2017 and using pooled ordinary least squares, fixed and random effects, IV regressions and the Generalized Method of Moments (GMM) finds that higher levels of inequality lead to greater control for corruption [17]. Similarly, Policardo and Carrera, examining a panel of 50 countries between 1995 and 2015 showed that the direction of causality between corruption and income inequality is country specific and can be bidirectional. Using a dynamic GMM model, the authors robustly find that income inequality positively affects corruption, while corruption does not seem to be significant in determining income inequality, contradicting the existing empirical literature on this topic. For Dusha, when wealth inequality is high, corruption is more prevalent, creating a persistent feedback between corruption and inequality [18].
Some stylised facts
It is worth noting that corruption remains endemic in SSA countries, although its extent varies from country to country. Although SSA countries have adopted anti-corruption strategies and laws, few have made progress, according to transparency international, in the global Corruption Perceptions Index (CPI) ranking since 2005. The CPI can range from 0 (high corruption) to 100 (very low corruption).
With an average score of 32 out of 100, sub-Saharan Africa lags behind other major regions of the world and shows no significant improvement in the corruption perceptions index [19]. The progress made by a handful of countries is overshadowed by the decline or stagnation of others and by the region's overall poor performance, with 44 of the 49 countries assessed in the 2022 index still scoring below 50. The Seychelles continues to lead the region with a score of 70 (23rd globally), followed by Botswana and Cape Verde, with a score of 60 (both 35th globally). Rwanda scores 51 (54th globally) and Mauritius scores 50 (57th). Globally, the countries with the lowest scores are largely SSA countries: Chad and Comoros (19), Burundi and Equatorial Guinea (17), South Sudan (13) and Somalia which occupies the last place globally with a score of 12. Moreover, some countries in the region have been declining significantly in recent years. Lesotho, for example, has gone from a score of 49 in 2014 to 37 in 2022; Liberia from 37 in 2016 to 26 in 2022 and Mali from 35 in 2015 to 28 in 2022 [20].
According to a UNDP study by Odusola et al., although Sub-Saharan Africa recorded an average reduction in its unweighted Gini coefficient, between 1991 and 2011, the region remains one of the least equal globally, with 10 of the most unequal countries in the world. These are: South Africa, Namibia, Botswana, Central African Republic, Comoros, Zambia, Lesotho, Swaziland, Guinea Bissau and Rwanda. The same study explores the dynamics and complexity of the income inequality issue by highlighting the presence of seven Sub-Saharan economies with extremely high levels of inequality, which it dubbed "the African outliers". These are: Botswana, Central African Republic, Comoros, Lesotho, Namibia, South Africa and Zambia. These countries, ranked among the most unequal on the continent, make Africa's Gini coefficient significantly higher than the world average. Figure 1 below shows the evolution of the share of national income held by the richest 10%, the richest 1% and the poorest 50% of countries in Sub-Saharan Africa from 1980 to 2016. This graph highlights the total value of these different trends. It shows that the richest 10% of Sub-Saharan Africa capture the largest share of total wealth (green area) while the poorest 50%, who are the most numerous, receive only a small share of total income (yellow area). For example, according to statistics during 2016 in Sub-Saharan Africa, the richest 1% of the region captured 17.79% of the total wealth produced while the poorest 50% captured only 12.15% of the total income. This shows how income inequality is a real Sub-Saharan problem (Figure 1).
Table 1 below presents the level and variation of the Corruption Indices (CPI) in 2002 and 2017 as well as the level and variation of the Income Inequality Indices (GINI) of the SSA countries considered.
The table reveals for several countries a positive relationship between the variation of the CPI and the variation of GINI: For countries like Burundi, Eritrea, Guinea Bissau, Mozambique, Sudan, South Africa, Congo, and Equatorial Guinea, a negative variation of the corruption index (meaning an increase in corruption) is accompanied by a positive variation of the income inequality index (increasing income inequality). Similarly, for countries such as Burkina Faso, Gambia, Malawi, Niger, Rwanda, Sierra Leone, Liberia, Madagascar, Angola, Cape Verde, Comoros, Cote d'Ivoire and Kenya, a positive variation in the corruption index (reduction of corruption) is accompanied by a negative variation in the income inequality index (decrease in income inequality) In addition, for many of the countries in the table there is a positive variation in the Gini index, which shows that the problem of income inequality is real in Sub-Saharan countries (Table 1).
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| SSA countries | CPI 2002 | CPI2017 | CPI Change 2002-2017 | GINI 2002 | GINI 2017 | GINI Change 2002-2017 |
| Burkina-Faso | 34 | 42 | +8 | 0.62 | 0.55 | -7 |
| Burundi | 23 | 22 | -1 | 0.56 | 0.57 | +0.01 |
| Eritrea | 26 | 18 | -8 | 0.5 | 0.57 | +0.07 |
| Ethiopia | 35 | 35 | 0 | 0.5 | 0.57 | +0.07 |
| Gambia | 25 | 30 | +5 | 0.64 | 0.54 | -10 |
| Guinea | 19 | 27 | +8 | 0.61 | 0.52 | -0.09 |
| Guinea Bissau | 22 | 17 | -5 | 0.54 | 0.68 | +0.14 |
| Malawi | 29 | 31 | +2 | 0.66 | 0.65 | -0.01 |
| Mali | 37.8 | 31 | -6.8 | 0.57 | 0.51 | -0.06 |
| Mozambique | 27 | 25 | -2 | 0.66 | 0.72 | +0.06 |
| Uganda | 27 | 26 | -1 | 0.64 | 0.61 | -0.03 |
| Niger | 22 | 33 | +11 | 0.62 | 0.52 | -10 |
| Rwanda | 31 | 55 | +24 | 0.68 | 0.62 | -0.06 |
| Sierra Leone | 22 | 30 | +8 | 0.59 | 0.52 | -0.07 |
| Sudan | 23 | 16 | -7 | 0.53 | 0.54 | +0.01 |
| Chad | 18 | 20 | +2 | 0.58 | 0.6 | +0.02 |
| Togo | 24 | 32 | +8 | 0.59 | 0.59 | 0 |
| Liberia | 22 | 31 | +9 | 0.54 | 0.53 | -0.01 |
| Madagascar | 17 | 24 | +7 | 0.62 | 0.6 | -0.02 |
| South Africa | 48 | 43 | -5 | 0,64 | 0.74 | +10 |
| Angola | 17 | 19 | +2 | 0.66 | 0.6 | -0.06 |
| Benin | 27 | 39 | 11 | 0.57 | 0.64 | +0.07 |
| Botswana | 64 | 61 | -3 | 0.78 | 0.69 | -0.09 |
| Cameroon | 22 | 25 | +3 | 0.6 | 0.63 | +0.03 |
| Cape Verde | 51 | 55 | +4 | 0.68 | 0.64 | -0.04 |
| Comoros | 23 | 27 | +4 | 0.71 | 0.61 | -0.1 |
| Congo | 22 | 21 | -1 | 0.64 | 0.66 | +0.02 |
| Cote d’Ivoire | 27 | 36 | +9 | 0.64 | 0.59 | -0.05 |
| Gabon | 33 | 32 | -1 | 0.6 | 0.54 | -0.06 |
| Ghana | 39 | 43 | +4 | 0.58 | 0.6 | +0.02 |
| Equatorial Guinea | 19 | 17 | -1 | 0.68 | 0.69 | +0.01 |
| Kenya | 19 | 28 | +9 | 0.64 | 0.58 | -0.06 |
| Lesotho | 34 | 39 | +5 | 0.66 | 0.69 | +0.03 |
| Mauritania | 31 | 28 | -3 | 0.57 | 0.5 | -0.07 |
| Namibia | 57 | 51 | -6 | 0.77 | 0.73 | -0.04 |
| Nigeria | 16 | 27 | +11 | 0.57 | 0.6 | +0.03 |
| Zimbabwe | 27 | 22 | -5 | 0.64 | 0.61 | -0.03 |
| Senegal | 31 | 45 | +14 | 0.59 | 0.57 | -0.02 |
| Tanzania | 27 | 36 | +9 | 0.56 | 0.55 | -0.01 |
Table 1. Variation of the Corruption Perception Index (CPI) and the GINI index for some SSA countries.
Theoretical model: The theoretical model of this work is inspired by the work of Fuentes et al. These authors have shown in their model that institutions can influence the long-term level of income inequality.
Empirical model, definition of variables and data source
Empirical model: Let yit be the variable to be explained, taking values between 0 and 1 for individual i,
i=1,…….,N during period t.
t=1,…….,T
xi=Vector of k explanatory variables.
The standard fractional regression model used in the cross-sectional context is defined by the following conditional expectation:
E(yi⁄xi)=G(xiθ) (1)
In equation (1), θ is the vector of the parameters of interest and G(.) is a nonlinear function. In the case of our study, G(.) takes the logit form (equation 2). Indeed, logit and probit models are the two forms that G(.) can take. But there is practically no difference between these two models. The only difference lies in the distribution of the error term which follows a normal distribution for the probit model and a logistic distribution for the logit model.

In a panel data setting, it is common to include time-invariant unobserved heterogeneity in the regression model. Let αi be individual effects, and φit it be time-varying unobservables. Ramalho et al., proposed the following empirical model under these conditions:
yit=G(xitθ+αi+φit) (3)
Inspired by equation (3), the following model is used for empirical testing, where G(.) is a Logit function:
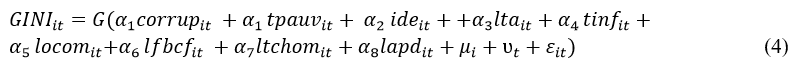
Equation (4) is the one that analyses the effect of corruption on income inequality. The study is carried out on 44 SSA countries and over the period 2002-2017. For this equation, the subscripts i and t represent countries and time. μi is the country specific effect, ʋt t the time-specific effect and ε the error term and corrup represents the different corruption indicators variables (corruption perception and corruption control).
Definition and description of variables, data source
The study uses world bank WDI (World Development Indicators) and WGI (World Governance Indicators) data, WID (World Inequality Database) data and transparency international data from 2002 to 2017 for 44 Sub-Saharan African countries. The choice of countries and study period is dictated by data availability constraints. Table 2 below presents the different variables used, their descriptions and the source of the data for these variables.
| Variables | Description of variables | Data source | |
|---|---|---|---|
| Variables | GINI | GINI is the Gini index and is used as a proxy for income inequality. These values are in the interval (0,1) and are taken from the WID database. The Gini index compares the income of each person with that of other people in the population. A value of 0 on this index means that each household has the same per capita income (perfect equality) and a value of 1 means that the total income of the group, for example a country, is captured by one household (perfect inequality). | WID (World Inequality Database) |
| Explanatory variables | cpi | cpi is transparency international's corruption perception index. The CPI provides the perception of business people and national experts of the level of corruption in the public sector. Scores range from 0 to 100 where 0 is the highest level of perceived corruption and 100 is the lowest level of perceived corruption. | Transparency International |
| gcc | gcc is the governance indicator for corruption control. It measures the strength and effectiveness of a country's political and institutional framework to prevent and combat corruption. These values are reported on a scale of 10, i.e., between 0 and 10, where 0 is the worst anti-corruption performance and 10 the best. | WGI (World Governance Indicators) | |
| ifbcf | Ifbcf is the logarithm of gross fixed capital formation. This indicator is considered as the public investment in basic infrastructure. | WDI (World Development Indicators) | |
| lapd | lapd is the logarithm of official development assistance. Official development assistance is assumed to accompany development investments. | WDI | |
| ide | ide is foreign direct investment. | WDI | |
| locom | locom is the logarithm of trade openness. It is the share of exports in GDP. It indicates how open the country is to foreign trade or how free from foreign trade it is. | WDI | |
| tinf | tinf is the inflation rate. The inflation rate is the percentage increase in the general price level over a year. | WDI | |
| itchom | chom is the logarithm of unemployment rate, which refers to the share of a country's labour force that is unemployed but available for and looking for work. | WDI | |
| ita | ita the logarithm of the illiteracy rate. The illiteracy rate is the total percentage of the population aged 15 years and over who can understand, read and write short statements about their daily lives. Generally, literacy also includes the ability to perform simple arithmetic operations. This indicator is calculated by dividing the number of literates aged 15 and over by the population of the corresponding age group and multiplying the result by 100. | WDI | |
| tpauv | tpauv the poverty rate. This indicator is often used as a proxy for absolute poverty. The poverty rate is the percentage of the population living with per capita consumption or income below a certain poverty line. In this work, the poverty rate is the ratio of the population of poor sub-Saharan Africa living on less than $1.90 per day (2011 PPP) (% of population). A value of 0 for this indicator means that there is no one living on less than $1.90 a day (no poor people in the population) and a value of 100 means that the entire population is poor. | WDI | |
Table 2. Definition and description of variables and data source.
Estimation method
Fractional Regression Method (FRM): In order to study the effect of corruption on income inequality in Sub-Saharan Africa, we rely on a Fractional Regression Model (FRM). The use of this estimation method is justified by the fact that when the values of the explained variable are between 0 and 1, the econometric literature indicates that the appropriate method for estimation is the FRM (Fractional Response Models) developed by Papke and Wooldridge. In the case of our work, the variable explained is income inequality. This variable is usually measured by the Gini index whose values belong to the interval (0,1). Thus, the FRM seems to be the most suitable estimation method for our work. The use of this method requires that the empirical model is well specified.
Generalized Moment Method (GMM)
The use of this method is justified by the fact that it allows us to control for individual and temporal specific effects and also to overcome simultaneity, reverse causality and omitted variables bias. In short, the GMM estimator allows for the correction of endogeneity problems in the model. Roodman indicates that when the data have a large number of countries (N) in relation to the period (T), the GMM difference estimator proposed by Arellano and Bond and the GMM-System estimator proposed by Arellano and Bover and Blundell and Bond are appropriate. Blundell and Bond have shown using Monte Carlo simulations that the GMM-System estimator performs better than the first difference estimator, the latter giving biased results in finite samples when the instruments are weak. Finally, it should be added that the panel GMM method has another advantage, it generates the instruments from the explanatory variables. In the case of our study where N=44 and T=16, the GMM in system seems to be appropriate.
Results of the estimations and interpretations
Descriptive statistics of the variables
Table 3 below presents the descriptive statistics of the variables used in the work
| Variable | Obs | Mean | Std. dev. | Min | Max |
|---|---|---|---|---|---|
| gcc | 704 | 0.313 | 0.862 | 0 | 4.867 |
| ipc | 704 | 3.109 | 1.152 | 1.1 | 9.1 |
| lfbcf | 704 | 7.286 | 3.815 | 0 | 10.85 |
| lapd | 704 | 8.535 | 0.607 | 5.362 | 10.052 |
| locom | 704 | 1.358 | 0.425 | 0 | 2.033 |
| lta | 704 | 0.285 | 0.65 | 0 | 1.975 |
| ide | 704 | 71140230 | 2.75E+08 | -9.76E+08 | 2.57E+09 |
| tinf | 704 | 6.735 | 8.515 | -8.975 | 108.897 |
| gini | 704 | 0.606 | 0.064 | 0.48 | 0.78 |
| tpauv | 704 | 4.57 | 1.624 | 0.497 | 6.921 |
| ltchom | 704 | 0.72 | 0.409 | -0.499 | 1.527 |
Table 3. Descriptive statistics of variables.
Estimation and interpretation of results
Before proceeding to the actual estimations, we perform the model specification test (Ramsey-Reset test) to see if the logit model used is well specified and that there are no omitted variables in the model. More specifically, the Ramsey-Reset test allows us to see if non-linear combinations of the fitted values help to explain the explained variable. The intuition behind the test is that if non-linear combinations of the explanatory variables have any power to explain the response variable, the model is misspecified. If the probability of the F-test is greater than 0.1, then the hypothesis of a good specification of the model cannot be rejected. The results of this test, as well as the results of the estimations, are reported in Table 4 below. The results of the Ramsey-Reset tests show that the model estimates are well specified (p-value >0.1).
| Explanatory variables | FRM method | GMM in two-stage system method |
|---|---|---|
| Corruption perception index (cpi) | 0.044*** (0.0086) |
|
| Corruption control (gcc) | -0.070* (0.037) |
|
| Poverty rate (tpauv) | 0.050*** (0.006) |
0.005 (0.014) |
| Gross fixed capital formation (ifbcf) | -0.004** (0,002) |
0.002 (0.002) |
| Official development assistance | 0.077*** (0.018) |
0.021 (0.02) |
| Inflation rate | 0.007 (0.001) |
0.0003 (0.0005) |
| Trade openness ( | 0.20*** (0.028) | 0.07** (0.032) |
| Illiteracy rate | 0.005 (0.013) | 0.002 (0.001) |
| Unemployment rate ( | 0.164*** (0.021) | 0.09** (0.036) |
| Foreign direct investment | 4.76e-11** (2.28e-11) | 1.06e-11 (2.44e-11) |
| Constant | 0.36** (0.177) | 0.633*** (0.152) |
| Number of observations | 704 | 660 |
| Ramsey–Reset test (p-value) | 0.3395 | - |
| Arellano-Bond test AR(2) (p-value) | - | 0.867 |
| Hansen test (p-value) | - | 0.996 |
Note: ***, ** and * indicate the significance of the variables at the 1%, 5% and 10% level respectively. Values in brackets are standard deviations. The explained variable is income inequality.
Table 4. Results of the estimates of the effect of corruption on income inequality (FRM and GMM methods).
It should also be noted that two tests are associated with the dynamic panel GMM estimator: The Sargan/Hansen over-identification test which tests the validity of lagged variables as instruments and the Arrellano and Bond autocorrelation test where the null hypothesis is the absence of second order autocorrelation of errors. According to these tables, the Hansen test and the Arellano and Bond second order autocorrelation test do not reject the hypothesis of the validity of the lagged variables as instruments and the hypothesis of the absence of second-order autocorrelation, respectively, because p-value >0.1. The model is globally robust.
The results of the FRM model indicate that the variable ipc which denotes the corruption perception index has a positive and significant effect on the Gini index. This means that an increase in the level of corruption leads to an increase in income inequality. In other words, the greater the perception by business people and national experts of the level of corruption in the public sector, the greater the gap between the incomes of 'rich' and 'poor' individuals. These results are consistent with those of Gyimah-Brempong and Dincer and Gunalp. Gyimah-Brempong has indeed shown, using panel data from selected African countries, that corruption is positively correlated with the level of income inequality as measured by the Gini coefficient. The results of his work indicate that a one-point increase in the corruption index leads to a seven-point increase in the Gini coefficient.
Dincer and Gunalp, observing the effects of corruption on income inequality using objective corruption data (the number of public officials convicted in a state for corruption related offences) for the US states, finds strong evidence that an increase in corruption leads to an increase in income inequality.
The positive effect of corruption on income inequality in SSA countries that we obtain can be explained by the fact that the benefits of corruption are likely to accrue to the best connected individuals belonging to the wealthiest groups and to a certain class of political figures. The best connected individuals are more likely to get the best public contracts, thus undermining the ability of governments to ensure a fair distribution of resources. When, for example, public money intended to build road infrastructure and markets in rural areas in SSA countries is diverted, this would slow down the income generating activities of the poorest people but rather increase the income of the better-off because these diverted funds can be invested in urban areas, where the better-off conduct their activities.
The results of the GMM model indicate that corruption control variable is significant and negatively affects the GINI index. This result means that better governance in terms of controlling or fighting corruption reduces income inequality. The more effective governance systems are put in place by the government to reduce corrupt practices in public and private administrations, the more the income gap between rich and poor decreases. This result supports the result obtained by the FRM method.
The results also show that control variables such as lfbcf, ide and lapd have negative and significant effects on the GINI index. These results imply that public investment, foreign direct investment and official development assistance contribute significantly to reducing income inequality in SSA countries. These results are consistent with those of Sane et al, and Lui et al. On the other hand, the locom variable has a positive and significant effect on the GINI index. This means that trade liberalisation increases income inequality in SSA countries. This result can be explained by the fact that international competition imposes efforts to be competitive, which involves downward pressure on the wages of the least qualified, especially those who are in direct competition with employees from all over the world and are more easily delocalized. Specialisation in high value added products leads to a need for skilled jobs, which pushes up the wages of the already better paid and thus widens the income gap between rich and poor.
Similarly, variables such as tpauv and tchom positively and significantly affect the GINI index. This means that unemployment and poverty are factors that further widen the income gap between rich and poor in SSA countries (Table 4).
From the perspective of institutional theory, corruption undoubtedly affects income inequality. Based on this theory, and the fact that previous studies have not revealed this effect of corruption on income inequality in sub-Saharan African countries, this paper empirically investigated the effect in SSA countries using larger data sets and robust methodologies. Using data from transparency international, the World Inequality Database (WID), the World Bank's World Governance Indicators (WGI) and World Development Indicators (WDI), the paper uses a Fractional Regression Model (FRM) and the Generalized Moment Method (GMM) with panel data to estimate the effect of corruption on income inequality for 44 countries in SSA from 2002 to 2017.
The results of the estimations through the FRM method indicate that corruption positively and significantly affects income inequality in SSA countries and those obtained through the GMM method indicate that good governance in controlling corruption in SSA countries negatively and significantly affects income inequality. Thus, the paper suggests that if the objective of SSA countries is to reduce income inequality, they will have to think and implement policies that can effectively fight corruption.
[Crossref]