Dynamic Behavioral Analysis of Two Plant Species through Mathematical Model

Abstract

In this paper the dynamic behaviour of two competing plant species is analyzed through mathematical model. The present approach is able to overcome the unrealistic theoretical basis and simplifies the interspecific competition processes of classical Lotka-Volterra competition equations. We discuss the interspecific competition between two plant species, namely Christella dentata and Christella parasitica in Kushmi jungle forest, Northern region of India. We obtained steady state solution, which were characterized by linearization method and analyzed.

Keywords

Mathematical model; Interspecific competition; linearization method; Lotka-Volterra competition

Introduction

Over the years it has been difficult to predict the consequences of population growth of plant species and this posed a problem to ecologist. Mathematical modeling has been a tool used by ecologist and has provided a reasonable approach to ecologist in the study of interaction of species. The remarkable variety of dynamical behaviors exhibited by many species (plants, insects and animals) has simulated great interest in the development of dynamical system models of populations [1,2]. In the 20^th century Lotka and Volterra derived Lotka-Volterra model for species competition. This model included the competition between two and more species called Interspecific competition. This model is of interest to ecologist because of its biologically meaningful parameters [3,4].

The competition between two different species at the same genus level, Christella dentata and Christella parasitica in Kushmi jungle, Northern part of India has been studied in the present work. Similar such work has also been done by Nevile. They have studied the complex interaction between two plant species in a harsh climate [5,6]. Yubin have worked on how to stabilize a mathematical model of interactions of n species population. Mark have considered mathematical model for biological invasion. Freekelston studied the determinants of the abundance of invasive annual weed. The dynamic of an annual pasture community was described from a five-year experimental and monitory study. Christian studied the plant competition experiments with variable plant density based on three published data sets [7,8].

Description

Mathematical formulation of model

This is described by the following differential equations. The two species Lotka-Volterra competition model is followed in this work for having density dependent growth and this makes it more realistic. The interaction of two species competing for some limited resources leads both plant species to competition, especially interspecific competition. A model can be used as an estimator of some parameter [9,10]. This approach carried the assumptions that the dynamics of the healthy meta populations can represent those of the endangered one and that the threats to the latter were external to population dynamics. Most dynamical system models which arise in practice are not amenable to exact solutions by known technique. Presently we follow the techniques which can be applied to analysis of almost any dynamical system model. These methods can provide important qualitative information about the behaviour of dynamical systems [11,12].

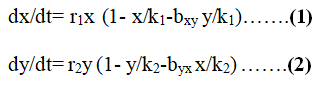
Where, x (t) is density of plant Christella parasitica at time t, y (t) is density of Christella dentata at time t.

r₁ and r₂ are intrinsic growth rates, k₁ and k₂ are carrying capacity of Christella parasitica and Christella dentata respectively.

b_xy measures competitive effect of y on x and b_yx measures competitive effect of x on y.

Steady-State Solution (SSS)

Characterization of steady-state solution

In order to investigate the stability of steady-state solution, we have linearlise competitive model (1) and (2) by obtaining Jacobian matrix. The characteristic equation is given by:

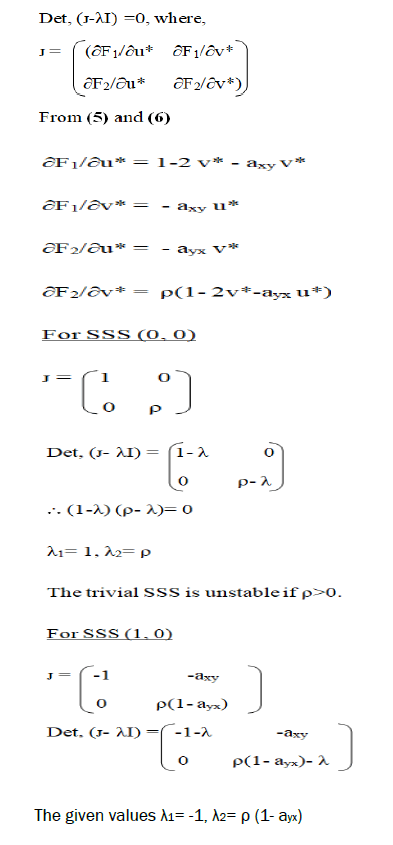
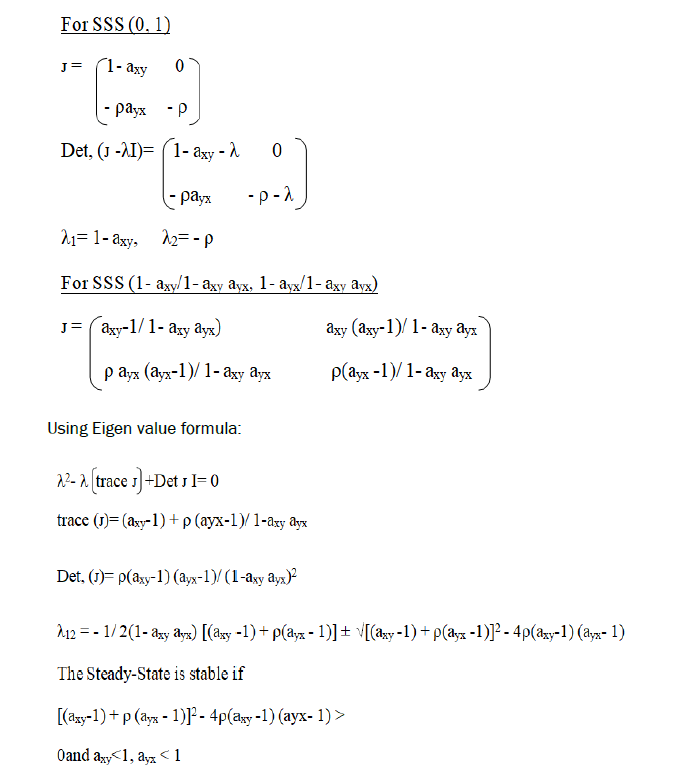
We got three stable solutions which are dependent on the a_xy, a_yx.

•a_xy>1, a_yx<1, growth of Christella parasitica and extinction of Christella dentata.
•a_xy<1, a_yx>1, then extinction of Christella parasitica and growth of Christella dentata.
•a_xy<1, a_yx<1, coexistence of two species.

Conclusion

Indeed, mathematical model has provided a good and reasonable approach to ecologist in the study of the interaction of plant species. Having considered the Lotka Volterra competition model we obtained four steady state solutions which were characterized using the Linearization method. We can say that the size of the parameters a_xy, a_yx, ρ will determine the stability of the steady state solutions.

References

1. Damgaard C. et al. Plant competition experiments: Testing hypotheses and estimating the probability of coexistence. Ecology. 1998;79:1760-1767.

   [Crossref] [Google Scholar]

2. Freckleton RP, et al. Determinants of the abundance of invasive annual weeds: Community structure and non-equilibrium dynamics. Proceedings of the Royal Society of London. Proc Biol Sci. 2000;267:1153-1161.

   [Crossref] [Google Scholar] [PubMed]

3. Glass L, et al. Stable oscillations in mathematical models of biological control systems. J Math Biol. 1978;6:207-223.  

   [Google Scholar]

4. Ford NJ, et al. Mathematical modelling of plant species interactions in a harsh climate. J Comp Appl Math. 2010;234:2732-2744.

   [Crossref] [Google Scholar]  

5. Yan Y, et al. Stabilizing a mathematical model of population system. J Franklin Inst. 2011;348:2744-2758.

   [Crossref] [Google Scholar]  

6. Krabs W. et al. A general predator-prey model. Math Comp Model Dyn Syst. 2003;9:387-401.

   [Google Scholar]  

7. Rafikov M, et al. Mathematical modeling and control of population systems: Applications in biological pest control. Appl Math Comp. 2008;200:557-573.

   [Crossref] [Google Scholar]  

8. Liou LP, et al. Global stability of a predator-prey system. J Math Biol. 1988;26:65-71.

   [Crossref] [Google Scholar]

9. Carson WP, et al. The role of litter in an old-field community: Impact of litter quantity in different seasons on plant species richness and abundance. Oecologia. 1990;85:8-13.

   [Crossref] [Google Scholar] [PubMed]

10. Claassen VP, et al. Annual and perennial grass growth on nitrogen‐depleted decomposed granite. Restor Ecol. 1998;6:175-180.

    [Crossref] [Google Scholar]

11. Lenz TI, et al. Direct and indirect effects of exotic annual grasses on species composition of a South Australian grassland. Austral Ecol. 2003;28:23-32.

    [Crossref] [Google Scholar]

12. Asfaw MD, et al. Effects of temperature and rainfall in plant-herbivore interactions at different altitude. Ecol Model. 2019;406:50-59.

    [Crossref] [Google Scholar]