DYNAMIC D-Q AXIS MODELING OF
THREE-PHASE ASYNCHRONOUS
MACHINE USING MATLAB

Shakuntla Boora; S.K Agarwal; K.S S; hu

DYNAMIC D-Q AXIS MODELING OF THREE-PHASE ASYNCHRONOUS MACHINE USING MATLAB

Shakuntla Boora¹, S.K Agarwal² and K.S Sandhu³

Assistant professor, Dept. of EE, YMCAUST, Faridabad, India
Professor and Head, Dept. of EE, YMCAUST, Faridabad, India
Professor and Head, Dept. of EE, National Institute of Technology, Kurukshetra, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents a dynamic d-q axis model of three- phase asynchronous motor in synchronously rotating frame. The systems of differential equations representing the dynamic state behaviours of the machine as developed are implemented in MATLAB/SIMULINK. The effects of the stepped sequence of mechanical loading on the motor output variables namely: three-phase stator currents (ia, ib and ic), electromechanical torque and rotor speed, d-q stator and rotor currents (iqs, ids, iqr and idr), d-q voltages (vqs and vds) are examined. The results obtained clearly show the elegance of the d-q axis transformation theory in machine modelling and the inherent limitations of the directon- line starting of 3-hp and 2250-hp asynchronous motors.

Keywords

dynamic modelling, asynchronous machine, synchronous reference frame, MATLAB/SIMULINK.

INTRODUCTION

The use of asynchronous motors particularly squirrel-cage rotor has increased tremendously since the day of its invention. They are being used as actuators in various industrial processes, robotics, house appliances (generally singlephase) and other similar applications. The reason for its day by day increasing popularity can be primarily attributed to its robust construction, simplicity in design and cost effectiveness, reliability, high efficiency and good self-starting capability [1-4]. The analysis of asynchronous motor is carried out in steady state whereby the machine is modelled as a second order electromechanical system.

Dynamic model describes the transient as well as the steady state behavior of the asynchronous machine. The model can be used to simulate the asynchronous motor drives and evaluate their transient performances including that of using the scalar control technique. This model is also essential when developing high performance control techniques for the aynchronous motor drives such as vector control or direct control (DTC) drives.

During start-up and other severe motoring operations, the asynchronous motor draws large currents, produce voltage dips, oscillatory torques and can even generate harmonics in the power system [5]. It is therefore important to be able to model the asynchronous machine in order to predict these phenomena. Various models have been developed and the qd axis model for the study of transient behaviour has been well tested and proven to be reliable and accurate [5, 6]. It has been shown that the speed of rotation of the d-q axis can be arbitrary although there are three preferred speeds or reference frames as follows [5]:

(a) The stationary reference frame when the d-q axes do not rotate.

(b) The rotor reference frame when the d-q axes rotate at rotor speed.

It is preferable to study multimachine system and stability analysis of controller design where the motor output equations must be linerized about an operating point in synchronously rotating frame [7]. In this frame, the steady state variables are constant and do not vary sinusoidally with time. In this paper, asynchronous machine model is described in the synchronously rotating frame [8] and also the effects of the stepped sequence of mechanical loading on the motor output variables are observed.

ASYNCHRONOUS MACHINE MODEL

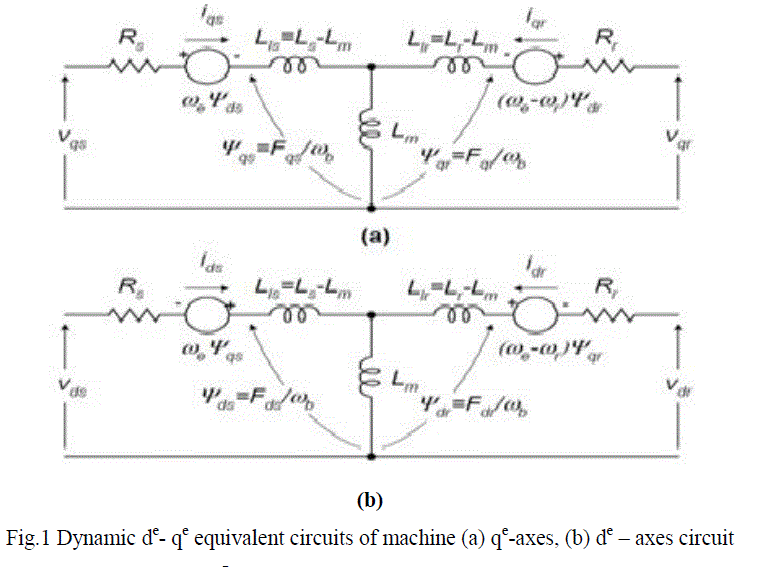
The asynchronous machine d-q or dynamic equivalent circuit is shown in fig. 1. The modelling equations in flux linkage form may be rearranged into the following form

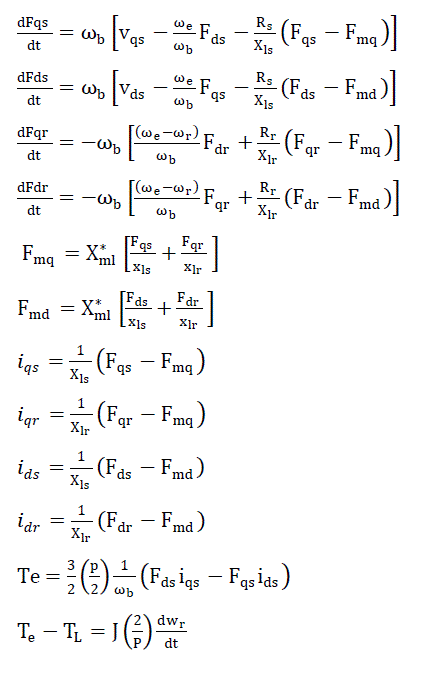For a squirrel cage asynchronous machine vqr and vdr in (3) and (4) are set to zero. An asynchronous machine model can be represented with five differential equations. To solve these equations, they have to be rearranged in the state space form. The state –space form can be achieved by inserting (5) and (6) in (1-4) and collecting the similar terms together so that each state derivative is a function of only other state variables and motor inputs. Then, the equations (1-4 and 12) of a squirrel-cage asynchronous motor in state-space become

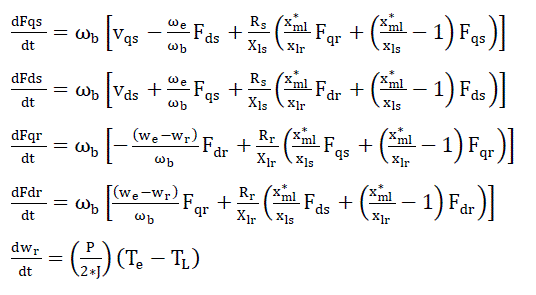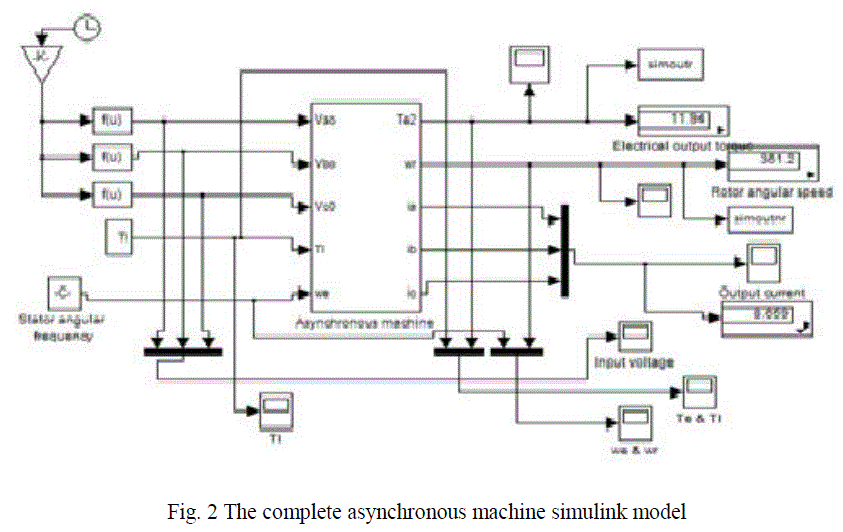
SIMULINK IMPLEMENTATION

The inputs of a squirrel cage asynchronous machine are the three-phase voltages, their fundamental frequency and the load torque. On the other hand the outputs are the three-phase currents, the electrical torque and the rotor speed. The Asynchronous machine model consists of five major blocks:

A. O-n conversion block

SIMULATION RESULTS

Two asynchronous motors: 3hp and 2250hp were tested in this simulated model [Appendix-I]. The results of the simulation are given for the first asynchronous motor:

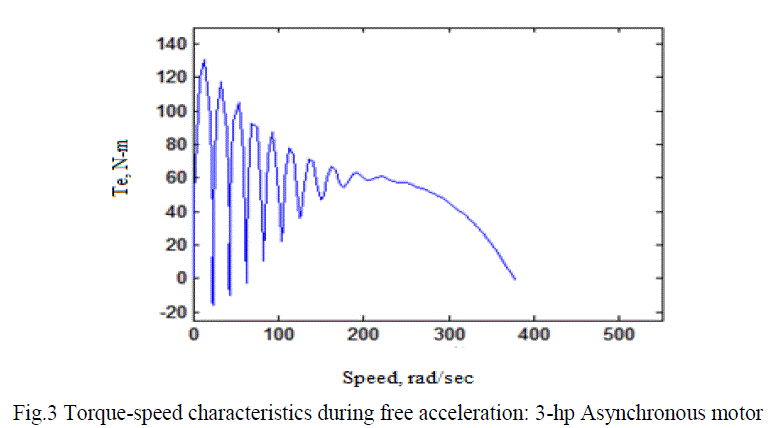
The 3hp machine is relatively high-slip machine; that is, rated torque is developed at a speed considerably less than synchronous speed [fig.3].

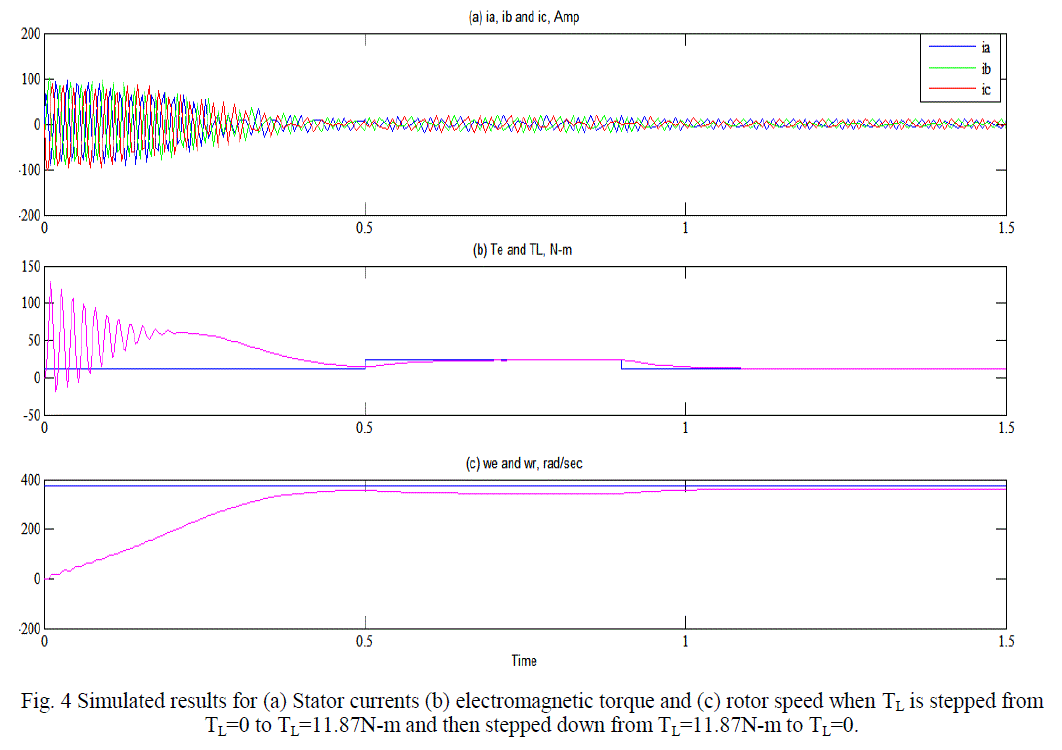
At stall, the input impedance of the asynchronous motor is essentially the stator resistance and leakage reactance in series with the rotor resistance and leakage reactance. Consequently with the rated applied voltage, the starting current is large, in some cases in the order of 10 times the rated value. This is observed in figure 4(a) and figures 8(a) and is a major limitation of the direct-on-line starting of the motor. It is therefore, recommended that reduced voltage starting methods such as star/delta, autotransformer and soft start methods be employed to reduce the excess starting current. It is observed in figure 4(c) that the rotor accelerates from stall with zero mechanical load torque and since friction and windage losses are not taken into account, the machine accelerates to synchronous speed. It can be seen from figure 4, that the machine has reached steady state at about 0.4 second. The application of 11.87 N-m mechanical loads at 0.5 seconds as illustrated in figure 4(b), results in sharp drop in the motor speed i.e. from 377 rad/sec to 361.2 rad/sec of figure 4(c) and an increase in the electromechanical torque upto 11.87 N-m in sympathy with the applied mechanical loading.

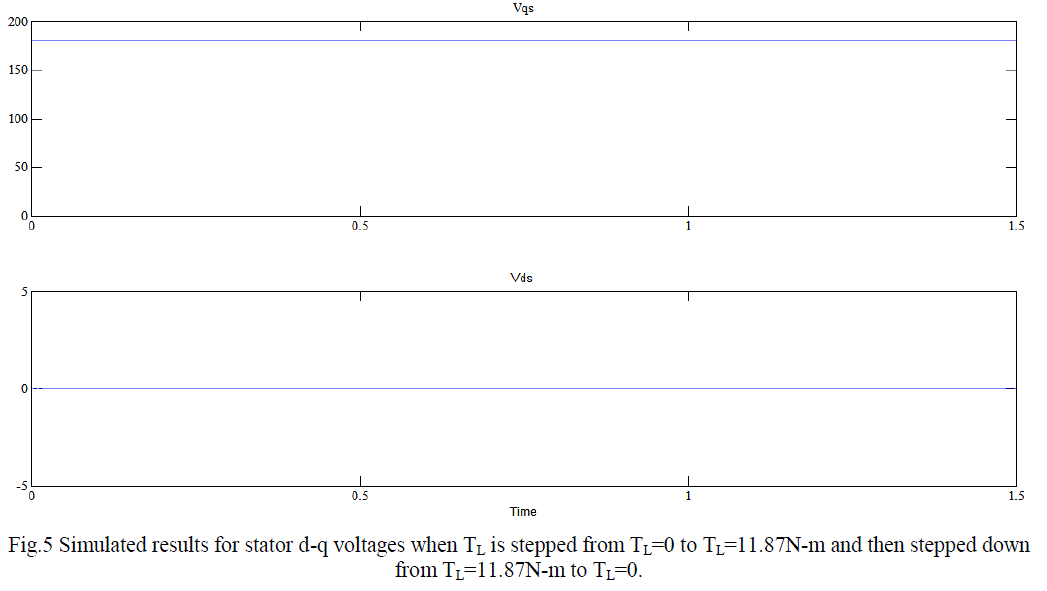
It is also observed from figure 5 that the stator q-axes voltage (vqs) = 179.6V = Vm (magnitude of supply voltage) and stator d-axis voltage (vds) = 0. It implies that the stator d-q voltages are DC quantities throughout the complete simulation time of 1.5 second.

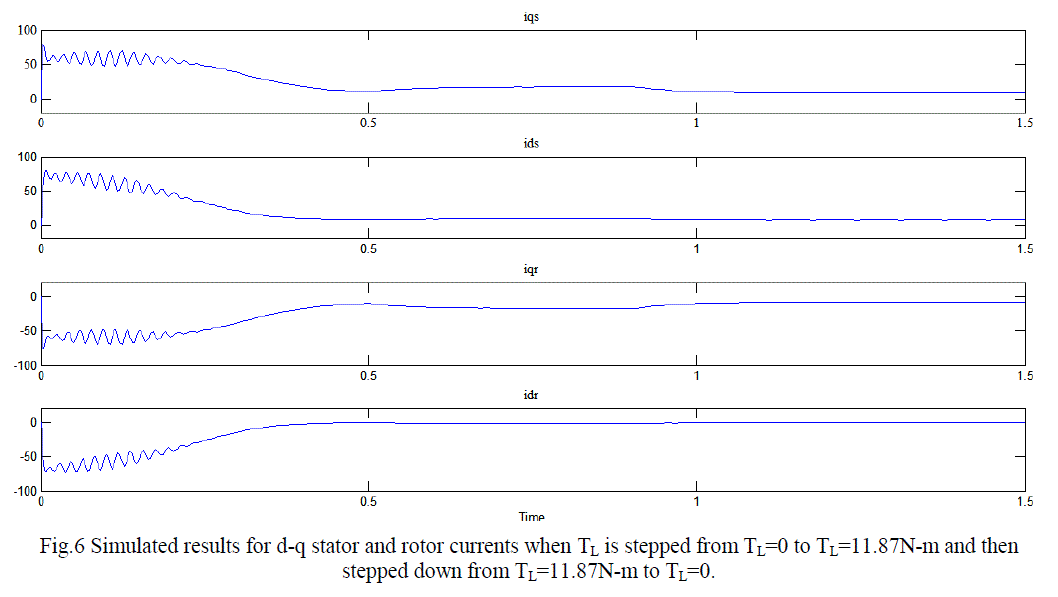
It is observed from figure 6 that the stator currents are DC quantities in the steady state at 0.4sec. The application of 11.87 N-m mechanical loads at 0.5 seconds as illustrated in figure 6, results in slight increase in DC currents. After removal of load at 0.9 sec, the stator d-q currents again appear as DC quantities.

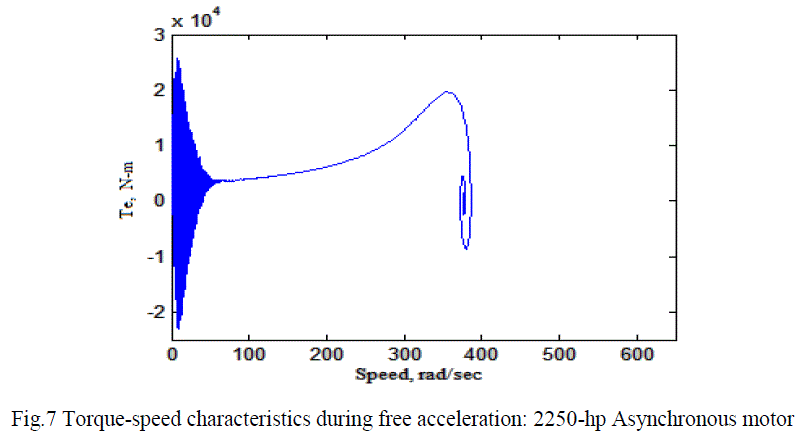
The results of simulation are also given for the other asynchronous motor: The 2250- hp machine is low slip machine; that is, rated torque is developed at synchronous speed as shown in figure 7.

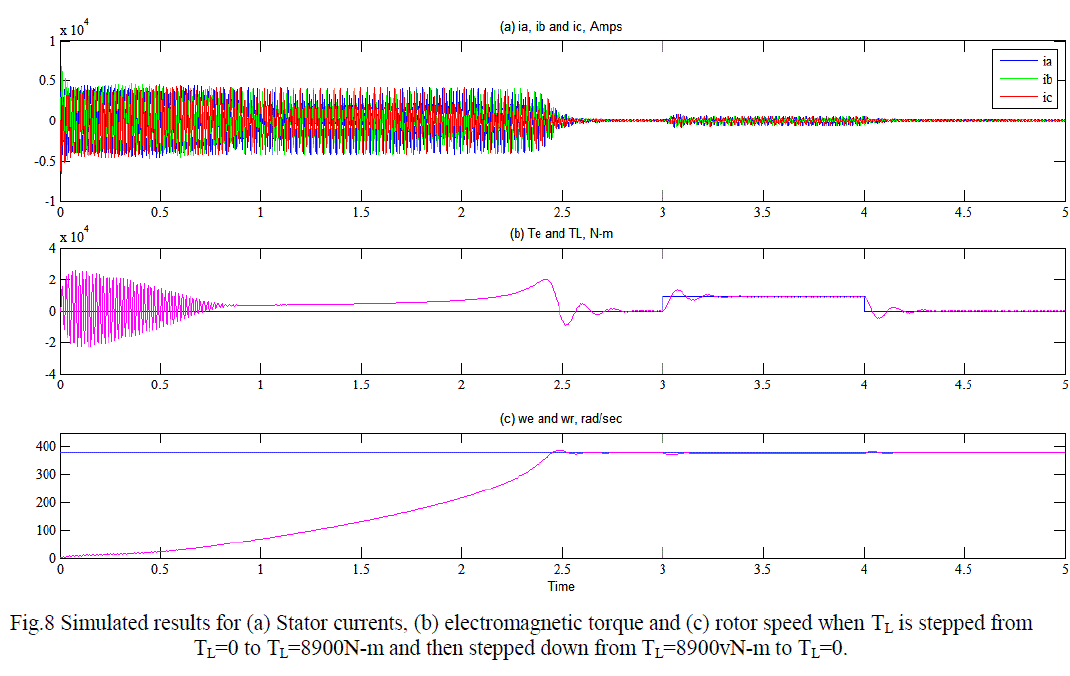
It is observed in figure 8(c) that the rotor accelerates from stall with zero mechanical load torque and since friction and windage losses are not taken into account, the machine accelerates to synchronous speed. It can be seen from figure 8, that the machine has reached steady state at about 2.8 second. The application of 8900 N-m mechanical load at 3 seconds as illustrated in figure 8(b), results in the same motor speed as synchronous speed of figure 8(c) and an increase in the electromechanical torque in sympathy with the applied mechanical loading.

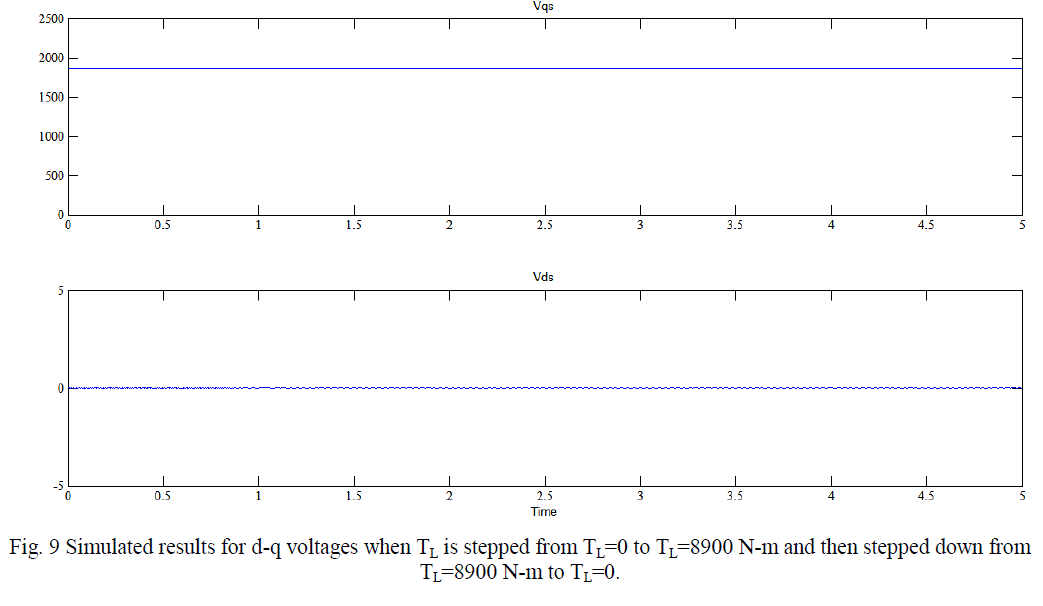
It is also observed from figure 9 that the stator q-axes voltage (vqs) = 1877.7V = Vm (magnitude of supply voltage) and stator d-axes voltage (vds) = 0. It implies that the stator q-d voltages are DC quantities.

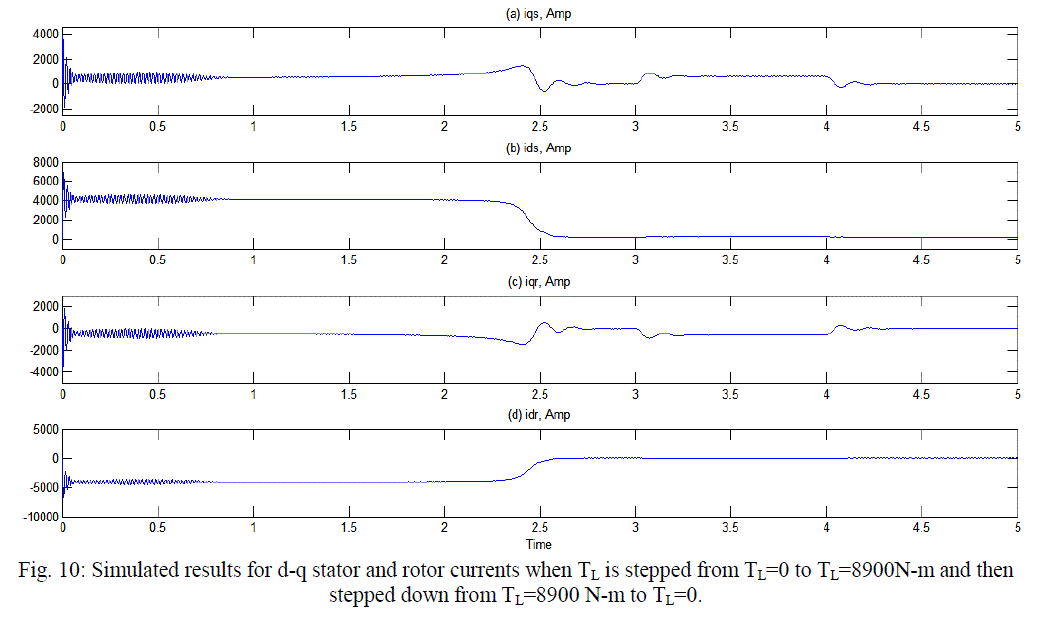
It is observed from figure 10 that the stator currents are DC quantities in the steady state at 2.9 sec. The application of 8900 N-m mechanical loads at 3 seconds as illustrated in figure 8, results in very slight increase in currents. After removal of load at 4sec, the stator q-d currents again appear as DC quantities.

All the simulations are running under the same condition as below:

Motor type: 3-hp and 2250-hp squirrel cage asynchronous motor

Simulation time: 1.5 seconds and 5 seconds

Solver type: ode45 (Demand-Prince)

Relative tolerance: 1e-3

CONCLUSIONS

For the analysis of dynamic behavior of the asynchronous machine, study of reference frames is essential. This paper has demonstrated the elegance of MATLAB/SIMULINK in the dynamic modeling and simulation of a 3-hp and 2250- hp asynchronous motor driving a mechanical load. The simulated motor is symmetrical and windage and friction losses are assumed negligible for ease of analysis. The results obtained clearly show the elegance of d-q axis transformation theory in machine modeling, inherent limitations of the direct-on-line starting of asynchronous motors and effect of mechanical loading on various motor output variables.

References

R. Krishan, “Electric motor drives: Modelling, analysis and control,” Prentice Hall Company, New Jersey, 2001.
K.L. Shi, T.F. Chan, Y. K. Wong and S. L. Ho, “Modeling and simulation of the three-phase induction motor using simulink,” International Journal of Electrical Engineering Education, vol. 36, pp. 163-172, 1999.
M.L. de Aguiar and M.M. Cad, “The concept of complex transfer functions applied to the modeling of induction motors,” IEEE Power Engineering Society Winter Meeting, vol. 1, pp. 387-391, 2000.
P.C. Krause, O. Wasynczuk, S.D. Sudhoff, “Analysis of electric machinery and drive systems”, IEEE Press, A John Wiley and Sons. Inc. Publication, Second Edition, 2002.
P.C. Krause, C.H Thomas, “Simulation of symmetrical induction machinery,” IEEE Trans. Power Apparatus and Systems, vol. PAS-84, no. 11, pp. 1038-1053, Nov1965.
Lee, R.J., Pillay, P., and Harley, R.G., “D, Q Reference frame for the simulation of induction motors”, Electric Power Systems Research Journal, vol. 8, pp.15-16, October 1984.
B.K Bose, “Modern power electronics and ac drives”, Prentice Hall, 2002.
B. Ozpineci, L.M. Tolbert, “Simulink implementation of induction machine model- A modular approach”, IEEE Int. Conf. Electric Machine and Drives, pp. 728-734, 2003.