Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Dynamic Economic Dispatch for Power Generation Using Hybrid optimization Algorithm

G.Karthika1, Mr.M.Vigneshwaran, M.E2
  1. PG Scholar, M. Kumarasamy College of Engineering, Karur, Tamilnadu, India
  2. Assistant Professor, M. Kumarasamy College of Engineering, Karur, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Dynamic Economic Dispatch (DED) problem is one of the most important ones in power system operation and planning. The main objective of the DED problems is to determine the optimal combination of power outputs of all generating units so as to meet the required demand at minimum cost while satisfying the all constraints. Conventionally, the cost function for each unit in DED problems has been approximately represented by a quadratic function and is solved using mathematical programming techniques. Commonly, these mathematical methods require some marginal cost information to find the global optimal solution. This paper proposes the evolutionary optimization technique namely Hybrid Genetic Algorithm-particle swarm optimization (HGAPSO), which is generic population based probabilistic search optimization algorithm using 6 bus system and can be applied to real world problem are respectively applied to solve an DED problem.

Keywords
Dynamic economic dispatch (DED), Hybrid Genetic Algorithm and Particle Swarm Optimization

INTRODUCTION
The Dynamic Economic Dispatch (DED) plays an important role in the operation of power system as well as real time control, and is of large significance in improving the economy and the reliability of the operation of power system. The DED approach has been successfully applied to minimize the production cost while satisfying the system demand and the operating limits of the generating units. Improve the reliability and efficiency of power systems, new communication technologies, and distributed energy sources, and demand response programs have been introduced [1]. These efforts are mainly motivated by the increasing costs of fossil fuels, environmental changes, and energy security concerns coupled with investments in the wind and solar generation to replace conventional co-emitting energy sources.
Over the years, many efforts have been made to solve the DED problem, incorporating different kinds of constraints or multiple objectives through various mathematical programming and optimization techniques. The conventional methods include Newton-Raphson method, Lambda Iteration method, Base Point and Participation Factor method, Gradient method etc [2]. Look-ahead dispatch is essentially a type of dynamic economic dispatch problem. A practical DED problem in look-ahead dispatch considers power balance constraints, spinning reserve constraints and transmission line flow constraints. Therefore, it is a large scale coupled spatial-temporal problem. DED has been studied and various techniques have been developed to solve this problem. Heuristics methods [3] are simple to implement and offer fast computational performance at the price of solution quality. In contrast, Dynamic Programming techniques [4] can provides global optimal solutions, but their practical use is limited by the curse of dimensionality. Modern optimization algorithms, including Simulated Annealing (SA) [5], Artificial Bee Colony (ABC) [6], Genetic Algorithm (GA) [7], Particle Swarm Optimization (PSO) [8][9], and others also have global search capabilities. However the performance of these procedures is greatly affected by the parameters.
In this study, configurations for GA and PSO in a fully coupled hybrid algorithm were investigated to achieve improvements in diversity and convergence simultaneously for application to real world engineering design problems [10]. In the new hybrid algorithm, GA is enhanced to obtain further diverse solutions than when used alone, while PSO is enhanced to perform faster convergence than when used alone. The results showed that the new hybrid algorithm has better performance than the other algorithm, in addition to either pure GA or pure PSO [11]. Especially the hybrid genetic algorithm-particle swarm optimization shows stable search ability regardless of selection of the initial population. HGAPSO is applied to different load demands and the results are compared to Simulated Annealing, Artificial Bee Colony, Genetic Algorithm and Particle Swarm Optimization [12].

PROBLEM FORMULATION
The dynamic economic dispatch problem is to allocate system load demand among committed generators over the schedule time horizon with minimal generation cost, while satisfying physical constraints and operating requirements. This problem can be formulated as nonlinear programming problem in mathematics. Total generation cost is the objective function to be minimized:
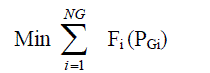image (1)
Where Fi (PGi) is usually expressed as a quadratic function in practice.
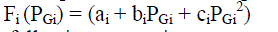image (2)
The minimization is subject to the following constraints.
Where
ai, bi and ci are the cost coefficients of the generator
NG is the number of generators including the slack bus.
PGi is the real power output of the ith generator(MW).
Fi(PGi) is the operating cost of unit i ( $/h).
1)Equality constraints
The equality constraints of the DED problems are represented by the power balance constraints, where the total power generation must cover the total power demand and the power loss.
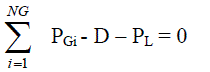image (3)
2)Inequality constraints
The inequality constraints reproduce the limits on physical devices in the power system as well as the limits created to ensure system security:
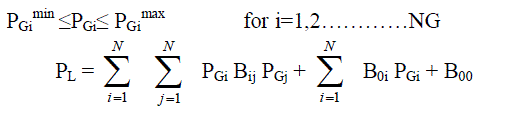image (4)

GENETIC ALGORITHM AND PARTICLE SWARM OPTIMIZATION
3.1 Basic concepts of Genetic Algorithms
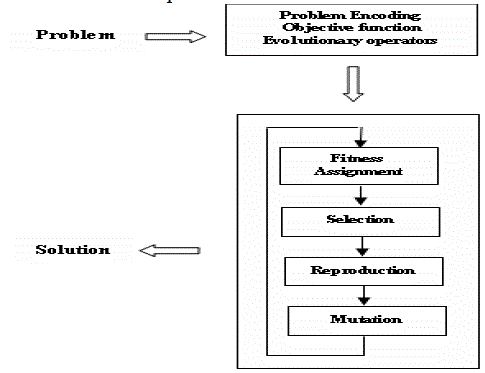
Genetic Algorithm (GA) is well known and frequently used evolutionary computation technique. The idea was inspired from Darwin’s natural selection theorem which is based on the idea of the survival of the fittest. The GA is inspired by the principles of genetics and evolution, and mimics the reproduction behavior observed in biological populations [13]. Genetic Algorithms are a family of computational models inspired by evolution. These algorithms encode a possible solution to a specific problem on a simple chromosome like data structure and apply recombination and mutation operators to these structures so as to preserve critical information.
The genetic algorithm can be viewed as two stage process. First one is the current population. Selection is useful to the current population to create an intermediate population. Then recombination and mutation are functional to the intermediate population to create the next population. The method of going from the current population to the next population constitutes one generation in the execution of a genetic algorithm.
Typically the mutation rate is applied with less than 1% probability. In some cases mutation is interpreted as randomly generating a new bit in which case, only 50% of the time will the mutation actually change the bit value. After the process of selection, recombination and mutation, the next population can be evaluated [14]. The process of evaluation, selection, recombination and mutation forms one generation in the execution of a genetic algorithm.
3.2 Particle Swarm Optimization
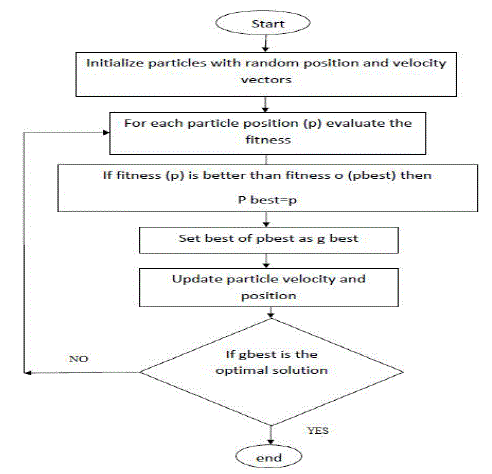
Particle swarm optimization (PSO) is one of the recent evolutionary optimization methods. Particle swarm optimization is a population based continuous optimization technique proposed by Kennedy and Eberhart (1995). Systems are initialized with a population of random solutions and searches for optima by updating generations [15]. However, unlike GA, PSO has no evolutionary operators, such as crossover and mutation. In the PSO, the potential solutions, called particles, move through the problem space by following the current optimum particles.
Particle Swarm Optimization can be used to solve many of the same kinds of problems as genetic algorithms. This optimization technique does not endure, however, from some of GA’s facilities; interaction in the group enhances rather than detracts from progress toward the solution. Further, a particle swarm optimization has memory, which the genetic algorithm does not have. Each particle keeps track of its coordinates in hyperspace which are associated with the best solution. This value is called Pbest. Another best value is also tracked. The “Global” version of the particle swarm optimizer keeps track of the overall best value, and its location, obtained thus far by any particle in the population. This is called Gbest. The particle swarm optimization concept consists of, at each time step, varying the velocity each particle toward its Pbest and Gbest. Acceleration is weighted by a random term, with divide random numbers being generated for acceleration toward Pbest and Gbest [16].
3.3 Hybrid Genetic Algorithm and Particle Swarm Optimization
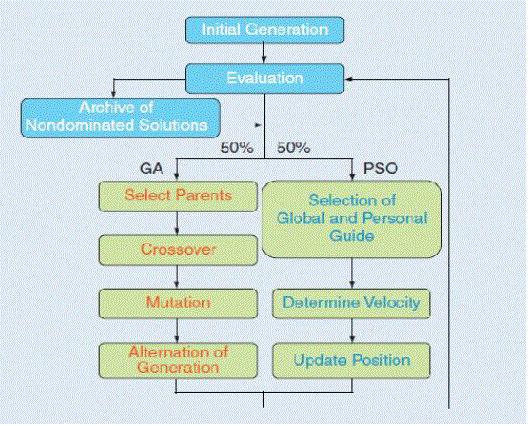
This new evolutionary learning algorithm is based on a hybrid of Genetic Algorithm (GA) and Particle Swarm Optimization (PSO), and is thus called HGAPSO. In HGAPSO, individuals in a new generation are formed, not only by crossover and mutation operation as in GA, but also by PSO [17]. The concept of elite strategy is adopted in hybrid genetic algorithm-particle swarm optimization (HGAPSO), where the upper half of the best performing individuals in a population is regarded as elites. However, instead of being reproduced directly to the next generation, these few selects are first enhanced. The group constituted by the few selects is enhanced by PSO, an operation which mimics the maturing occurrence in nature. These enhanced elites constitute half of the population in the new generation, where as the other half is generated by performing crossover and mutation operation on these enhanced elites.
First multiple solutions are generated randomly as an initial population and objective function values are evaluated for each solution. After the evaluation, the population is divided into two sub-populations one of which is updated by the genetic algorithm operation, while the other is updated by particle swarm optimization operation. New solutions created by each operation are combined in the next generation, and non-dominated solutions in the combined population are archived [18]. The archive data are shared between the GA and PSO, i.e., non-dominated solutions created by the PSO can be used as parents in GA, while non-dominated solutions created by GA can be used as global guides in PSO. Originally, PSO works based on social adaptation of knowledge, and all individuals are considered to be of the same generation. On the contrary, GA works based on evolution from generation to generation, so the changes of individuals in a one generation are not considered. Successful applications of PSO to several optimization problems, like function minimization and feed forward neural network design have demonstrated its potential.

OPTIMIZATION RESULTS AND DISSCISSION
The effectiveness of the simulated algorithm, artificial bee colony algorithm, genetic algorithm, and particle swarm optimization and hybrid genetic algorithm-particle swarm optimization algorithms are tested on a six generator systems at different loads.
4.1 OUTPUT FOR DEMAND 800
4.1.1 Cost Analysis Output
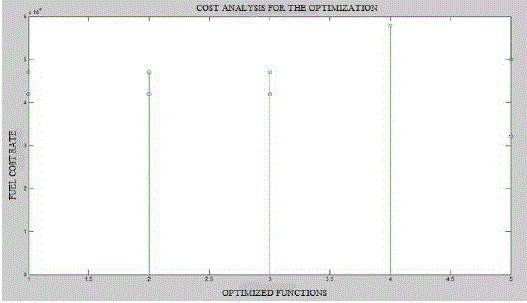
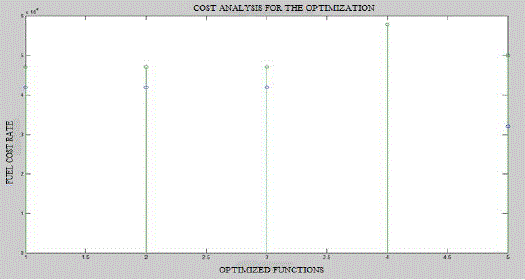
The cost analysis for the load 800 is shown in figure 4.1. This figure shows the various optimization algorithms corresponding to the fuel cost rate. The point 1,2,3,4 and 5 denotes the various algorithms are: simulated annealing, artificial bee colony algorithm, genetic algorithms, particle swarm optimization and hybrid genetic algorithm-particle swarm optimization algorithm. Comparing these algorithms hybrid genetic algorithm-particle swarm optimization only reduced the sufficient fuel cost. So this is the best optimization algorithm to solve the economic dispatch problem.
4.1.2 Time Analysis Output
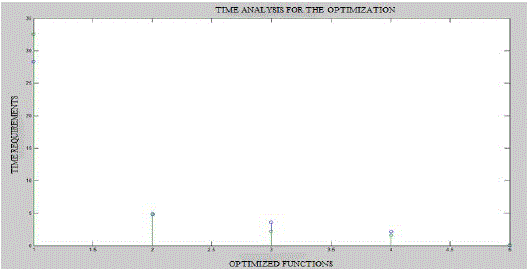
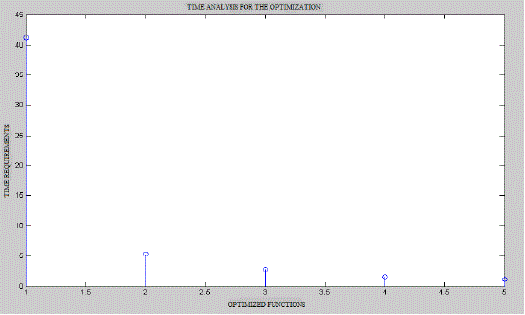
The time analysis for the load 800 is shown in figure 4.2. This figure shows the various optimization algorithms corresponding to the time requirements. The point 1,2,3,4 and 5 denotes the various algorithms are: simulated annealing, artificial bee colony algorithm, genetic algorithm, particle swarm optimization and hybrid genetic algorithm-particle swarm optimization algorithm. Comparing these algorithms hybrid genetic algorithm-particle swarm optimization only reduced the time. So this is the best optimization algorithm to solve the economic dispatch problem.
4.2 OUTPUT FOR DEMAND 900
4.2.1 Cost Analysis Output
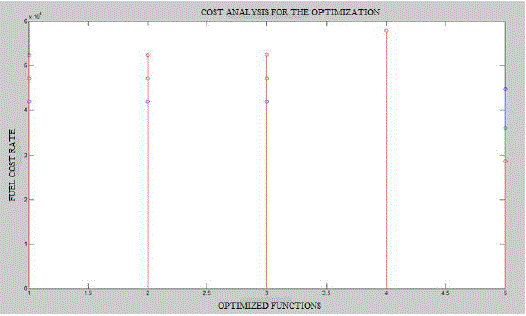
The cost analysis for the load 800 is shown in figure 4.3. This figure shows the various optimization algorithms corresponding to the fuel cost rate. The point 1,2,3,4 and 5 denotes the various algorithms are: simulated annealing, artificial bee colony algorithm, genetic algorithm, particle swarm optimization and hybrid genetic algorithm-particle swarm optimization algorithm. Comparing these algorithms hybrid genetic algorithm-particle swarm optimization only reduced the sufficient fuel cost. So this is the best optimization algorithm to solve the economic dispatch problem.
4.2.2 Time Analysis Output
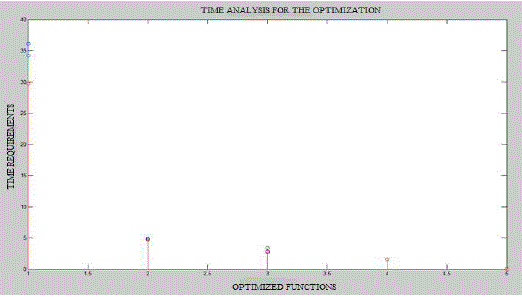
The time analysis for the load 900 is shown in figure 4.4. This figure shows the various optimization algorithms corresponding to the time requirements. The point 1,2,3,4 and 5 denotes the various algorithms are: simulated annealing, artificial bee colony algorithm, genetic algorithm, particle swarm optimization and hybrid genetic algorithm-particle swarm optimization algorithm. Comparing these algorithms hybrid genetic algorithm-particle swarm optimization only reduced the time. So this is the best optimization algorithm to solve the economic dispatch problem.
4.3 OUTPUT FOR DEMAND 1000
4.3.1 Cost Analysis Output
The cost analysis for the load 1000 is shown in figure 4.5. This figure shows the various optimization algorithms corresponding to the fuel cost rate. The point 1,2,3,4 and 5 denotes the various algorithms are: simulated annealing, artificial bee colony algorithm, genetic algorithm, particle swarm optimization and hybrid genetic algorithm-particle swarm optimization algorithm. Comparing these algorithms hybrid genetic algorithm-particle swarm optimization only reduced the sufficient fuel cost. So this is the best optimization algorithm to solve the economic dispatch problem.
4.3.2 Time Analysis Output
The time analysis for the load 1000 is shown in figure 4.6. This figure shows the various optimization algorithms corresponding to the time requirements. The point 1,2,3,4 and 5 denotes the various algorithms are: simulated annealing, artificial bee colony algorithm, genetic algorithm, particle swarm optimization and hybrid genetic algorithm-particle swarm optimization algorithm. Comparing these algorithms hybrid genetic algorithm-particle swarm optimization only reduced the time. So this is the best optimization algorithm to solve the economic dispatch problem.
4.4 OUTPUT FOR DEMAND 1100
4.4.1 Cost Analysis Output
The cost analysis for the load 1100 is shown in figure 4.7. This figure shows the various optimization algorithms corresponding to the fuel cost rate. The point 1,2,3,4 and 5 denotes the various algorithms are: simulated annealing, artificial bee colony algorithm, genetic algorithm, particle swarm optimization and hybrid genetic algorithm-particle swarm optimization algorithm. Comparing these algorithms hybrid genetic algorithm-particle swarm optimization only reduced the sufficient fuel cost. So this is the best optimization algorithm to solve the economic dispatch problem.
4.4.2 Time Analysis Output
The time analysis for the load 1100 is shown in figure 4.8. This figure shows the various optimization algorithms corresponding to the time requirements. The point 1,2,3,4 and 5 denotes the various algorithms are: simulated annealing, artificial bee colony algorithm, genetic algorithm, particle swarm optimization and hybrid genetic algorithm-particle swarm optimization algorithm. Comparing these algorithms hybrid genetic algorithm-particle swarm optimization only reduced the time. So this is the best optimization algorithm to solve the economic dispatch problem.
5.1 COST ANALYSIS FOR 6-GENERATOR SYSTEM
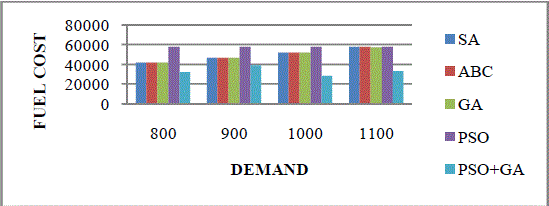
The various algorithms fuel cost for different loads are shown in table 5.1.
The fuel cost for various algorithms and different loads are shown in figure 5.1. comparing all algorithms and all different loads , the fuel cost will be reduced in hybrid genetic-particle swarm optimization method. So this is the best optimization technique in dynamic economic dispatch to solve the problem.
5.3 TIME ANALYSIS FOR 6-GENERATOR SYSTEM
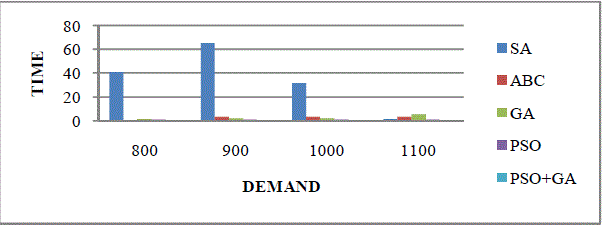
The various algorithms time duration for different loads are shown in table 5.3.
The time duration for various algorithms and different loads are shown in figure 7.3. comparing all algorithms and all different loads , the time will be reduced in hybrid genetic-particle swarm optimization method. So this is the best optimization technique in dynamic economic dispatch to solve the problem.

CONCLUSION
In this work, the formulation and implementation of solution methods to obtain the optimum solution of dynamic economic dispatch using genetic algorithm and particle swarm optimization is carried out.
Particle swarm optimization can be used to solve many of the same kinds of problems as genetic algorithms. This optimization technique does not suffer, however, from some of GAs difficulties: interaction in the group enhances rather than detracts from progress toward the solution. Further, a particle swarm optimization has memory, which the genetic algorithm does not have. Change in genetic population’s results in destruction of previous knowledge of the problem, except when mainly disapproving is employed, in which case usually one or a small number of individuals retain their “identities”. In particle swarm optimization, individuals who fly past optima values are tugged to return toward them; knowledge of good solutions is retained by all particles. Particle swarm optimization has also been demonstrated to perform well on genetic algorithm test functions, and it appears to be a capable approach for robot task learning.
The effectiveness of the developed program is tested for six generators test system. The results obtained from these methods are also compared with each other. It is found that hybrid optimization algorithm is giving better results than other optimization techniques.
 

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4
Figure 6 Figure 7 Figure 8 Figure 9
Figure 1 Figure 2 Figure 3 Figure 4
Figure 10 Figure 11 Figure 12 Figure 13
 

References