ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Sonakshi Gupta1 and Dr. Sulochana Wadhwani2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This paper presents Synchronously Rotating Reference Frame dynamic modeling of the induction motor using MATLAB/SIMULINK. The dynamic behavior of the machine is represented by the system of the differential equations. Computer based simulation of induction machine has certainly opened new horizons for the performance analysis. A good mathematical model is helpful in determining the behavior of the induction machine under different load conditions and in selecting appropriate machine for the specific application. The model describes in this paper can be used for the steady state and transient analysis of the squirrel cage induction motor.
Keywords |
| 3-ÃÂÃ⢠Induction motor, dynamic modeling, parameter estimation, MATLAB/SIMULINK, Reference Frames, D-Q Model |
INTRODUCTION |
| An induction motor is one of the most often used electric machines in high performance drive applications. Squirrel cage induction motor is popularly known as the work-horse of the modern industry. It is due to its simplicity in design, robust construction, reliability, tremendous self-starting capability and high-efficiency. |
| Induction motors are highly nonlinear and electric rotor variables are not measurable. The skin effect in the rotor winding and iron core saturation lead to even bigger complications in the modeling process of the machine [7]. Traditionally dynamic parameters are estimated by performing no-load test and locked-rotor test. Due to the complication of dynamic behaviors of induction motors, inaccuracy of transient characteristics may obtain while using these dynamic parameters [5]. These tests are not convenient because they require human electrical measurements and intervention on the machine. The locked rotor test results in very high slip frequency, and increasing skin effect influence on the rotor resistance. This leads to incorrect operating conditions and inaccurate parameter estimation. |
| In this research work synchronously rotating reference frame dynamic modeling of the induction motor is used. The induction machine is represented mathematically using the two-axis theory of electric machines. The two-phase signal representation is often used to reduce the complexity of the differential equations that describes the induction machine. Complexity of these equations can also be reduced by eliminating all time varying inductances, due to electric circuits in relative motion, from the voltage equations of the machine. The time varying voltage and torque equations describe the dynamic behavior of the induction motor. [1, 2] |
LITERATURE SURVEY |
| The literature of this research paper has been taken from the R. Krishan, “Electric motor drives: Modelling, analysis and control,” Prentice Hall Company, New Jersey, 2001;Bimal K.Bose, “Modern Power Electronics and AC Drives,”Prentice Hall India, 2005. Some research papers have also been referred. These papers are P.C. Krause and C. H. Thomas,“ Simulation of Symmetrical Induction Machinery”, IEEE Transaction on Power Apparatus and Systems, Vol. 84, November 1965, pp. 1038-1053; M. L. de Aguiar, M. M. Cad, “The concept of complex transfer functions applied to the modeling of induction motors”, Power Engineering Society Winter Meeting, 2000, pp. 387–391; Boonaruang Marungsri, Nittaya Meeboon , Anant Oonsilvilia “Dynamic Model Identification of Induction Motors using Intelligent Search Techniques with taking Core Loss into Account”, Proceedings of the 6th WSEAS International Conference on Power Systems, Lisbon, Portugal, September 22-24, 2006 etc. |
DYNAMIC MODELLING |
| When three phase induction motor is started and during the other transient operations of induction motor its draws large currents, which produced voltage drips, oscillatory torques and even generate the harmonics in the power systems. The dq axis model is more reliable and accurate to investigate such of these problems. The dynamic model is derived by using two-phase motor in direct and quadrature. This approach is useful because of the conceptual simplicity obtained with two set of windings one is on the stator and other is on the rotor. [3] The three-phase stationary reference frame (a-b-c) into two-phase reference frame (d-q-0) is carried out by following equation [4] |
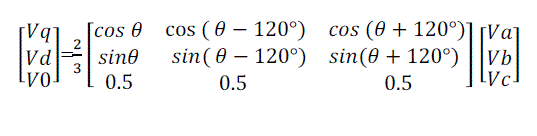 (1) (1) |
| where Va, Vb, Vc are the three phase stator voltages of an induction machine under balanced condition. Va, Vb, Vc can be expressed as: |
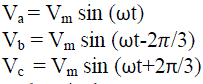 (2),(3) & (4) (2),(3) & (4) |
| and V0 is the zero sequence component, which may or may not be present. |
| Figure 1: shows the d-q axis representation of the induction motor in which q-axis of stator and rotor is perpendicular to the d-axis of the stator and rotor respectively. |
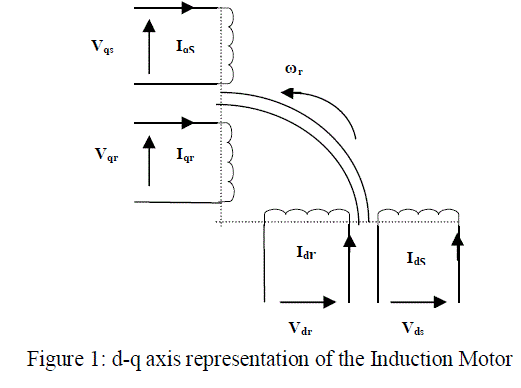 |
| The dynamic model of induction machine plays a vital role in the validation of design process of the motor-drive systems, eliminating inadvertent design mistakes and the resulting errors in the prototype constructions and testing. [6] Dynamic model includes three preferred speeds or reference frames as follows: |
| (a) The stationary reference frame when the d-q axes do not rotate. |
| (b) The rotor reference frame when the d-q axes rotate at rotor speed. |
| (c) The synchronously rotating reference frame when the d-q axes rotate at synchronous speed. [1] |
| The transient dynamic behavior of three phase squirrel cage induction motor can be analyzed by using any one of the mentioned three reference frames. If the stator voltage is unbalanced or discontinuous and the rotor voltages are balanced, the stationary reference frames is useful. If the rotor voltages are unbalanced or discontinuous and stator voltages are unbalanced or discontinuous and stator voltages are balanced, the rotor reference frames is used. And if stator and rotor all voltages are balanced and continuous, then synchronous reference frame is used. [8] |
| The voltage balance equation for the dq0 coil in arbitrary reference frame is: |
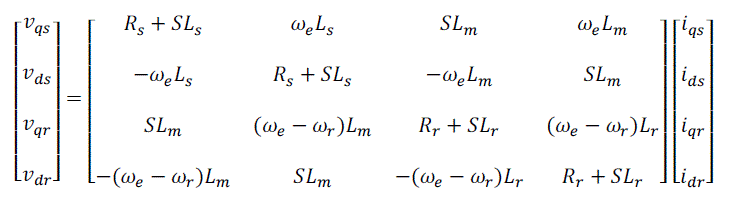 (5) (5) |
MODELLING IN DIFFERENT FRAMES |
| In stationary reference frame, the speed of the reference frame is zero i.e., ωe = 0. Hence the resulting model will be |
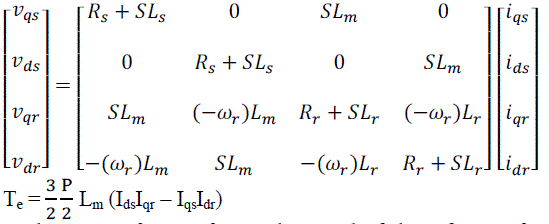 (6) & (7) (6) & (7) |
| In the rotor reference frame, the speed of the reference frame is ωe = ωr, and angular position is θc-θr. Hence the resulting model will be |
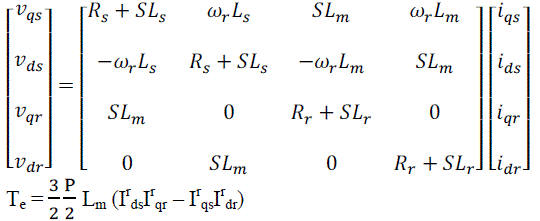 (8) & (9) (8) & (9) |
| In synchronous frame, the speed of the reference frame is ωe = ωs, and angular position θc = θr = ωst. Hence the resulting model will be |
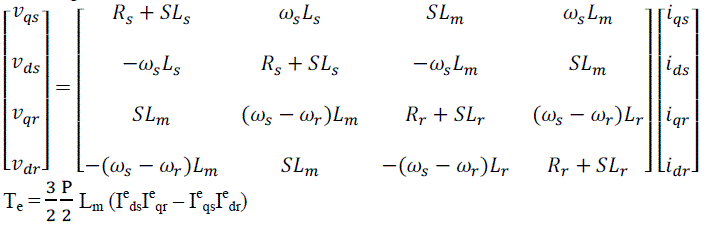 (10) & (11) (10) & (11) |
SIMULATION RESULTS AND DISCUSSION |
| Two asynchronous motors: 3hp and 2250hp were tested in the simulated model which is shown in Figure 2. |
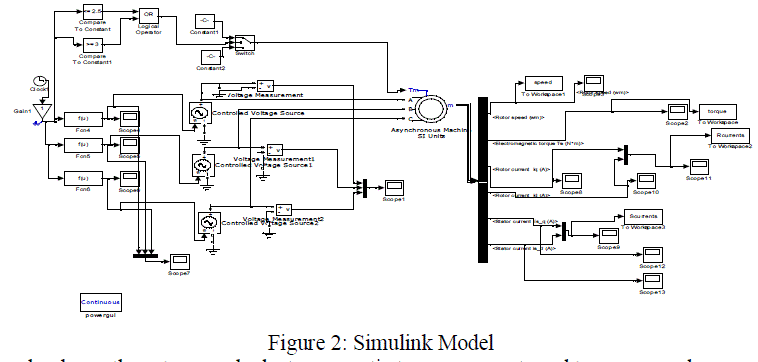 |
| The following graphs shows the rotor speed, electromagnetic torque, currents and torque- speed curve of both the machines |
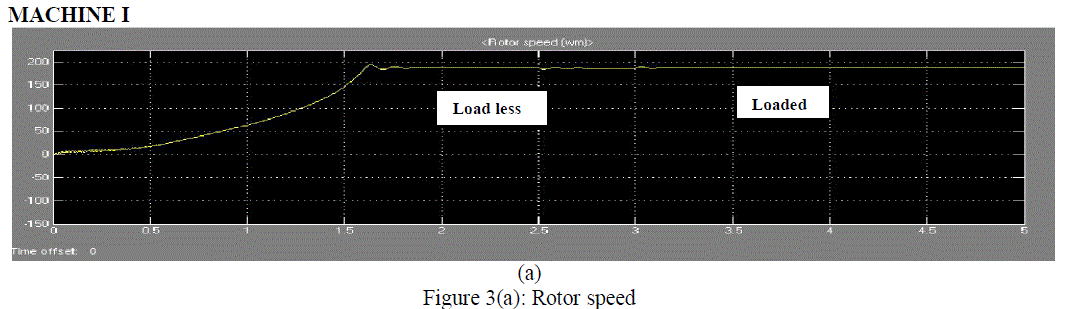 |
| Figure 3(a) shows the rotor speed graph with respect to the time for the machine I. For the time 0 to 2.5 seconds the speed is accelerating and for the time 2 to 2.5 seconds it is load less and then it is loaded with torque 9000Nm. The rotor accelerates from stall with zero mechanical load torque; since friction and windage losses are not taken into account. It can be observed from the figure that the machine operates at a speed very close to the synchronous speed when operating on the no-load. After reaching the synchronous speed (in case of no-load condition) the larger machine’s speed will overshoot, this will take some time to stabilize at around the synchronous speed. |
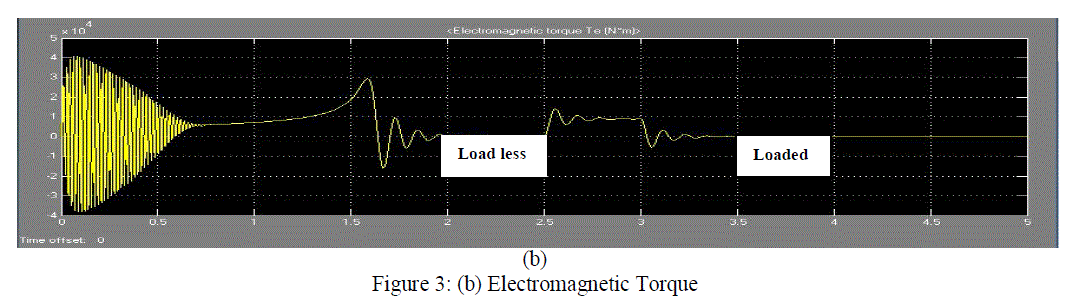 |
| Figure 3(b) shows the electromagnetic torque graph with respect to the time. For the time 2 to 2.5 seconds it is load less and then it is loaded with torque 9000Nm. The transient oscillation of torque for a load change from no load torque to rated torque condition is observed. Transients occur more during the load less condition rather than the loaded condition. |
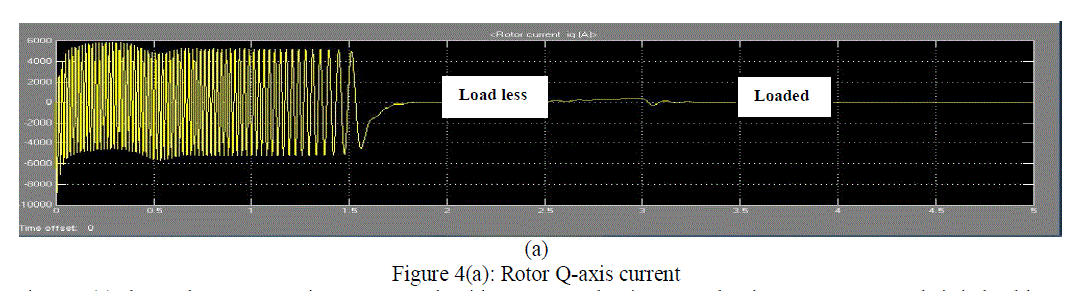 |
| Figure 4(a) shows the rotor Q-axis current graph with respect to the time. For the time 2 to 2.5 seconds it is load less and then it is loaded with torque 9000Nm. The current is variable time 1 to 1.5 seconds. Current transient also occurs during the load less condition rather than the loaded condition. |
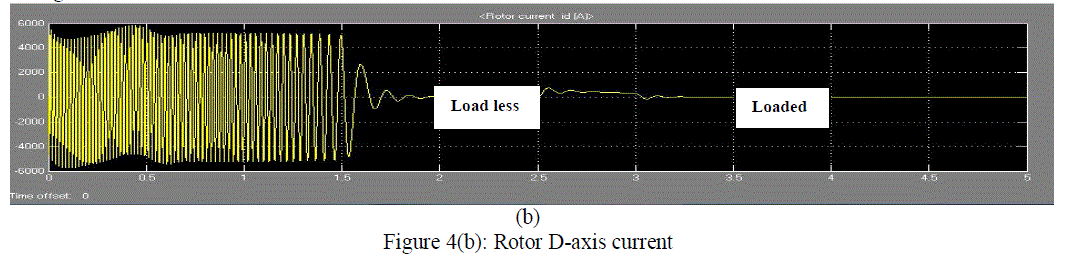 |
| Figure 4(b) shows the rotor D-axis current graph with respect to the time. For the time 2 to 2.5 seconds it is load less and then it is loaded with torque 9000Nm. The current is variable time 1 to 1.5 seconds. Current transient also occurs during the load less condition rather than the loaded condition. |
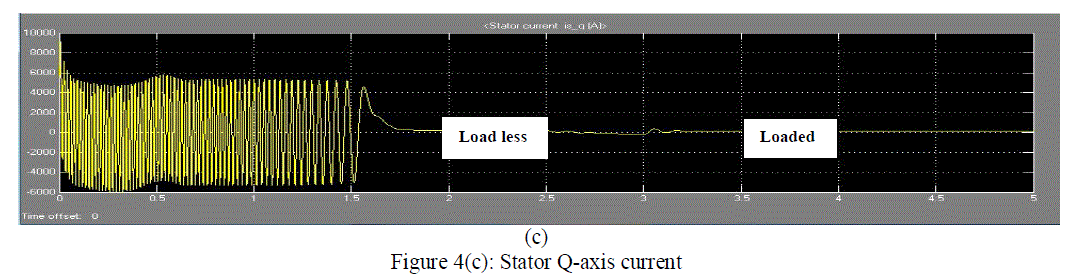 |
| Figure 4(c) shows the stator Q-axis current graph with respect to the time. For the time 2 to 2.5 seconds it is load less and then it is loaded with torque 9000Nm. The current is variable time 1 to 1.5 seconds. Current transient also occurs during the load less condition rather than the loaded condition. |
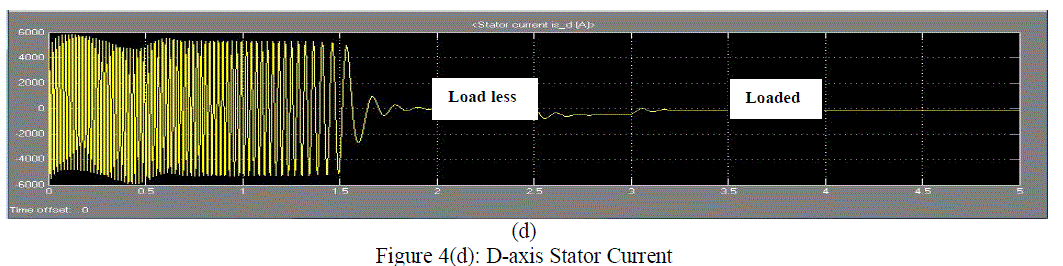 |
| Figure 4(d) shows the stator D-axis current graph with respect to the time. For the time 2 to 2.5 seconds it is load less and then it is loaded with torque 9000Nm. The current is variable time 1 to 1.5 seconds. Current transient also occurs during the load less condition rather than the loaded condition. |
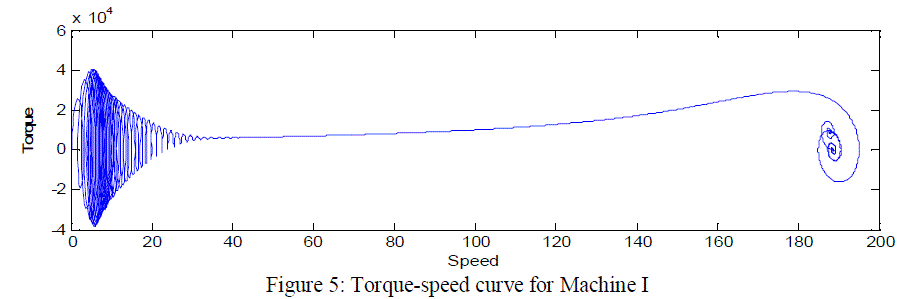 |
| Figure 5 shows the graph between torque and the speed for the bigger machine. The 2250hp machine is relatively high slip machine; that is, rated torque is developed at a speed considerably more than the synchronous speed. It can be seen that oscillatory behavior of the smaller machine is much more acceptable than that of the larger machine. |
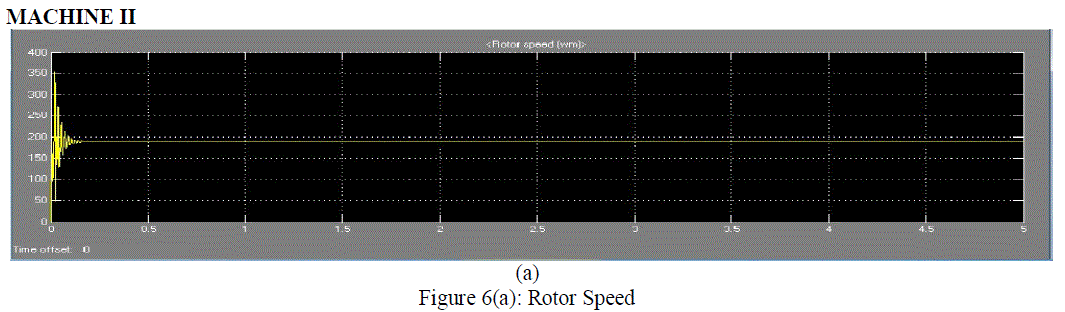 |
| Figure 6(a) shows the graph of the rotor speed for the machine II i.e, for the smaller machine in which the loaded torque is 11.87Nm. The motor is variable for the very short time. It is observed that transients occur in the machine for very short time for the load less condition and then machine runs at the synchronous speed. |
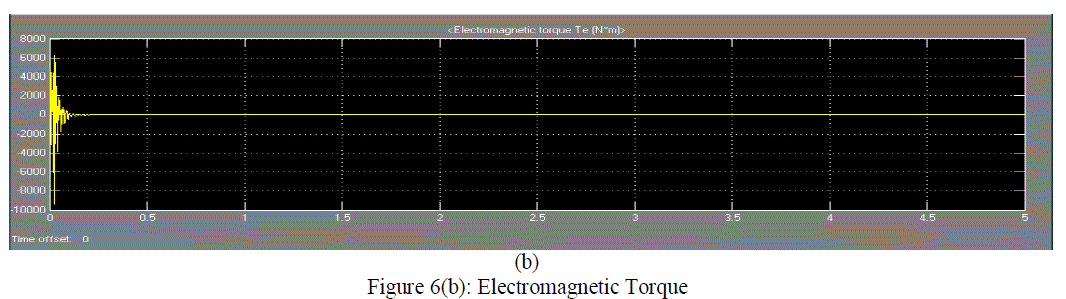 |
| Figure 6(b) shows the electromagnetic torque graph with respect to the time. The loaded torque is 11.87Nm. The motor is variable for the very short time. It is observed that transients occur in the machine for very short time for the load less condition and then machine runs at the synchronous speed. |
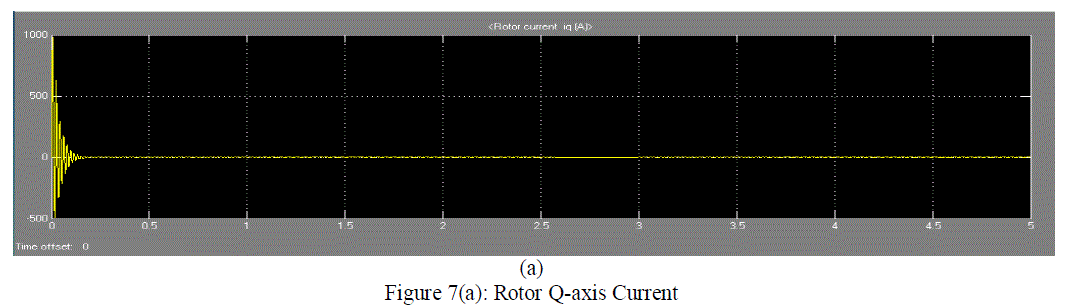 |
| Figure 7(a) shows the rotor Q-axis current graph with respect to the time. The current is variable for the short time. It is observed that the after transients the rotor current behave as the dc currents. A slight variation in the current waveform occurs during the loaded condition. |
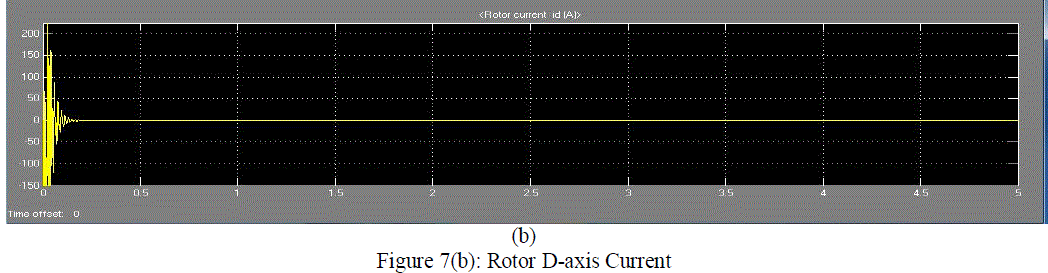 |
| Figure 7(b) shows the rotor D-axis current graph with respect to the time. The current is variable for the short time. It is observed that the after transients the rotor current behave as the dc currents. A slight variation in the current waveform occurs during the loaded condition. |
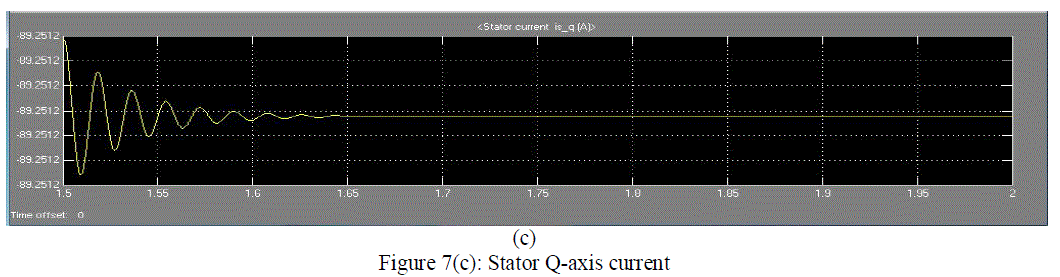 |
| Figure 7(c) shows the stator Q-axis current graph with respect to the time. The current is variable for the time 0 to 1.6 seconds. It is observed that stator currents are DC quantities in the steady state. |
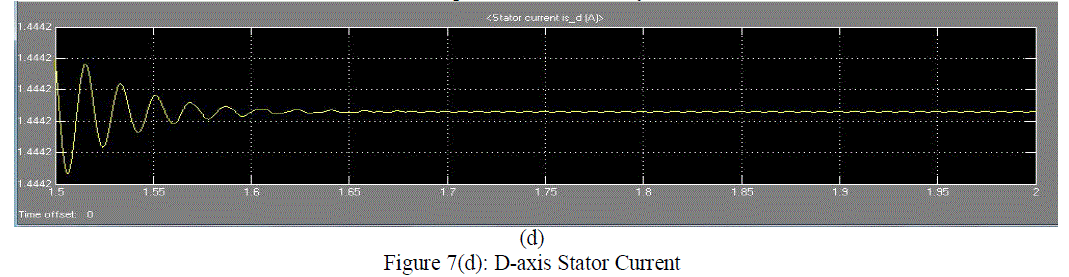 |
| Figure 7(d) shows the d-axis stator current graph with respect to the time. The current is variable for the time 0 to 1.6 seconds. It is observed that stator currents are DC quantities in the steady state. |
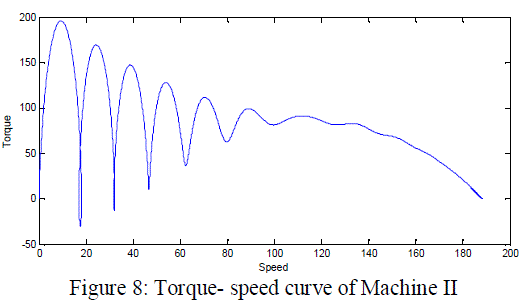 |
| Figure 8 shows the graph between torque and the speed for the smaller machine. The 3hp machine is relatively high slip machine; that is, rated torque is developed at a speed considerably less than the synchronous speed. It can be seen that oscillatory behavior of the smaller machine is much more acceptable than that of the larger machine. |
CONCLUSION |
| In adjustable speed drives, the transient behavior of the induction motor has to be taken into consideration. Hence, to study the dynamic behavior of the induction motor under both transient and steady state conditions, accurate mathematical models of the induction motor have been developed in the different reference frame by using d-q modeling. The above model is quite dynamic and competent in simulating during the sudden change in load. Moreover, d-q modeling is popular approach for the practical implementation of vector controlled induction motor drives. |
References |
|
 |