Research & Reviews: Journal of Engineering and Technology
MenuISSN: 2319-9873
ISSN: 2319-9873
+44 7456 035580Rawaa Jawad*, Eyad I Abbas, Sundus D Hasan
Department of Electrical Engineering, University of Technology, Baghdad, Iraq
Received: 06-Oct-2020, Manuscript No. JET-23-13190; Editor assigned: 09-Oct- 2020, Pre QC No. JET-23-13190 (PQ); Reviewed: 23-Oct-2020, QC No. JET-23- 13190; Revised: 02-Jun- 2023, Manuscript No. JET-23-13190 (R); Published: 30-Jun-2023, DOI: 10.4172/2319-9857.12.2.001
Citation: Jawad R, et al. Dynamic Particle Swarm Optimization Algorithm for Intelligent Mobile Robot Path Finding System. 2023;12:001.
Copyright: © 2023 Jawad R , et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Research & Reviews: Journal of Engineering and Technology
This study investigate application for Particle Swarm Optimization (PSO) to robot mobility problem to determine a shortest path possible with minimum time required to move from starting point to target point in ergonomics with obstacles. In this paper, algorithm is used to chart global path. A proposed algorithm reads ergonomics expressed by network model and creates an ideal collision-free path. Simulation studies have proven a effectiveness for proposed algorithm to chart path for mobile robot. This study showed how to optimize a path planning for an intelligent mobile robot by making optimal use for a PSO technology work environment with obstacles. A basis for this study is societal behavior Birds flow and raise fish. This concept is powered by Swarm intelligence, and is one for a famous research fields in a field for computational swarm intelligence, as a particle swarm improvement algorithm (PSO). Important notes have been made portable robots are greatly affect by path finding problem and solution is being developed for How to solve this problem., this study suggests a good solution that can produce high-quality and effective portable robots. PSO technology has been adapted to provide effective solution to path finding problems.
Particle swarm optimization; Path finding; Intelligent mobile robot; Portable; Algorithm
A robotic is necessary element in society today's. Many frequently jobs, and without used human facility. A word for robots are utilize in wide range for mechanical mobility machine [1]. Path finding for mobile robot, located in environment with obstacles, is define to find path for robot that reach from source to destination no hitting for obstacle, topics as shortness for path and simple is Quality standards to select path. Determining path from completing is divided two types for constraint satisfaction and accurate. A first type is finding an optimal path or assuming are is no path which means it consumes time, so a second type finds an appropriate path in short time[2].
Many researcher study a mobile robot as present neural networks for mobile robot to path planning, parameters take for training time, network performance and possible distance are considered after repetition to achieve a dataset using a Probability Road Map algorithm (PRM). 36% improvement in a possible distance achieves a use for a neural network, and compares it with a traditional PRM algorithm. Present path planning utilized A QR code sticker, QR code sticker placed in a floor, robot extract, data stored in an onboard camera sticker and navigate according to this detail. Both a predicted device and wheel encoders used to measure in path domestic details for a robot. A machine tested in simulator WEBOTS and a simulation result showed performance and less machine complexity [3].
Proposed path planning using mixed Artificial Potential Field (APF) and Ant Colony Optimization (ACO) based on grid map ispr under established setting for mobile robot. As well as APF is improved in three methods: A field for attraction, a resultant force for movement and a jumping out for an infinite loop. Hybrid approach combines global update with local residential updates for desi. A ACO optimisation process was split into phases. So, a direction for a resulting force shows enhanced APF which applied inspired factors and leads an ant colony to move in a directional manner. So inspired factor is ignored and changes from ant colony are entirely dependent on pheromone updating, which can resolve resistance for ant colony and compel am to pursue new and better routes. An experiment result show that method is stronger stability and environmental adaptability [4].
Path finding
Since 1980, many research employment to solve issues for mobile robots path planning. By applied two ways as: Firstly using global scenario, obstacle information and characteristics for robot. Second way collects local information during sensor and explain path traversing problem. Developing effective trajectory planning employ optimization technique to strike trade-forf between reactive to environmental events. Finding a path to a robot is a common problem in portable robots. A robot should be able to move itself from a start location to a target location without colliding with obstacles. So an important research in navigation robot, that find universally optimized. A path from starting point to target in particular environment. At a same time avoid collisions. That's where a path is optimized. Means that a path must meet certain criteria such as length. A path is shorter or power consumption for a robot is a lowest or a time required to reach a goal is minimal etcs. Many artificial intelligence techniques and algorithms have been used to find path as (Fuzzy, ANN, ANFIS, ACO, PSO, Bee colony, Genetic ) [5].
Artificial intelligence techniques
Artificial Intelligence (AI) has been tremendous develop in recent years. It is thriving research area with increase number for research important and technology basic area for increase number application area. So algorithmic innovation. Artificial intelligences are being using to increase sciences and technologies because for its amazing capability for dealing at high information, complexity, high accuracy and fast delivery. Artificial Neural Network (ANN); fuzzy logic; Neuro Fuzzy Interference System (ANFIS); Genetic Algorithm (GA); Particle Swarm Optimization (PSO); etc. are familiar artificial intelligence tools; AI has been used in many areas such as medicine, engineering, finance, economics, computing and so forth [6].
Particle swarm optimization
A basic model appears to a world for PSO algorithms by Kennedy and Eberhart by proven problem solving complex nonlinear optimization for bird flock imitation behavior. Ay generate function-optimization principle which means particle swarm [7]. Believe a N-dimensional global equilibrium define as formula:
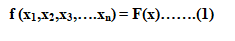
Where xi is search variable, that represent a set for free variable at given function.
Multiagent parallel search technique is a Particle Swarm Optimization (PSO) algorithm that maintain swarm for particles so each particle presents potential solution in swarm. Like whole particles fly when looking for multidimensional space, each particle changes its location as its own experience and neighbors [8]. So xit Indicate a particle position vector in a multidimensional space search phase time, a search space also updates a position for particle by:
Where:vit+1 is vector for particle velocity which process optimization and reflect both own and social experience knowledge from whole particles. So, in PSO technique, every one particle is initiated at random and evaluate fitness compute to gear for finding best personal (best value for every particles) and best global (best value for particle in entire swarm) [9]. As well as a loop start for find optimum solution. In oar hand, first velocity for particle is updated by bests for personal and global, and also each position particle is updated by current velocity. So, loop is ended for stopping predetermined criterion in advance [10]. Mainly, PSO algorithms have been developed two types, global best (gbest) and local best (lbest) that differ in size for neighborhoods as show in Figure 1. A global best PSO is a technique anywhere position for every particles are influenced by best-fit particle in entire swarm. Thus Pbest it is main for note that best personal in individual particle that visited since first time step for gbest PSO technique, velocity for particles (i) is determined as:
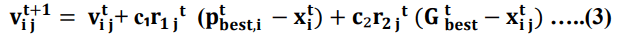
Where:
vijt+1 vector velocity for particles (i) in dimension (j) at time t xijt vector position for particles (i) in dimension (j) at time t Ptbest (i) best personal position for particles (i) in dimension (j) found at initialization through time t Gtbest best global position for particles (i) in dimension (j) found at initialization through time t
c1 and c2: are constant positive acceleration that utilized level involvement for cognitive and social component correspondingly
r1jt and r2jt are number random at uniform distribution at time t
Figure 1: Structure for particle swarm optimization.
PSO algorithm parameters
Swarm size: Population size is defined a number for particles n in swarm. A large swarm generates larger part for space search for covered per iteration. Large number for particle may decrease number for iteration that require for find good optimization results , this algorithm range from 150 to 300 as a number for particles [11].
Iteration numbers: Number for iteration to find a good result s are problem-dependent. A too small number for iteration may stop process search prematurely, but too large iteration is consequence add unnecessary complexity computational and required more time in this algorithm taken many iteration [12].
Acceleration coefficients: c1 and c2, with random values r1 and r2, continue stochastic effected for cognitive and social component respectively for velocity particle. A constant c1 presented how much assurance particle is in itself, but c2 give how much confidence particle is in its neighbors [13].
Inertia weight: ω, is measured replace for adjusting influence for velocities previous in process, i.e. it control momentum for particle using weighing contribution for velocity previous. A weigh inertia ω at each step be multiplied by velocity at previous time step, i.e. Vi j So, in gbest PSO, equation velocity for particle with weight inertia changes at formula (4) (Figure 2).
Figure 2: Algorithm for a proposed robotic path finding.
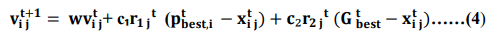
Steps for PSO
A PSO approach is illustrated in a following steps: Step 1: (Modeling environment and algorithm obstacles); this paper is represented by a network based model, a mobile robot world with a number for obstacles; a square dimensional (2D) model with a uniform pattern. A grid based model allows for distance measurement and barrier representation simulation is applied to a work environment to ensure PSO efficiency. An inside for a grid is blue, where a mobile robot will move as obstacles and overcome am in a best way. No unit is used to calculate a length for a path, since each cell in environment that presents in any unit. A square in area for robot's start and star is location for a target. Table 1 displays a grid scale, starting point and target point coordinates.
Table 1 displays a number for obstacles for a world. A higher a number for obstacles, a algorithm will require more generations forget best solution. Obstacle areas are represented by a circular blue (static obstacle) and red obstacle (dynamic obstacle). And have an average area of obstacle robs=(0.5 0.7 0.8 0.4 0.5 0.6) units where area of obstacle dynamic 0.4 units. A boundaries for a obstacle region are considered to be its actual limits as well as a safety distance which is calculated taking into account a size for a robot whose route is sought show in Figure 3 and Table 2.
| Variables | Values |
|---|---|
| Grid size (unit) | 6 ×6 |
| Start point (xs , ys) | (0,0) |
| Target point (xt , yt) | (4,6) |
| Number of obstacles | 6 |
Table 1. Presented a size for grid with point for start and target and obstacles number.
Figure 3: Working environment.
| Number of obstacle | xobs | yobs | robs |
|---|---|---|---|
| 1 | 1.5 | 5 | 0.5 |
| 2 | 3 | 3 | 0.7 |
| 3 | 1 | 1.5 | 0.8 |
| 4 | 1.5 | 3 | 0.4 |
| 5 | 3 | 1.5 | 0.5 |
| 6 | 0 | 3 | 0.6 |
Table 2. Coordinates of obstacles.
Step 2: Initialize a swarm for particles starting position A starting point for path for each particle, first A location and velocity for every particle is created randomly, but it is limited to search area limits .A particle location is held in an array where I is a particle number. A matrix rows corresponds to both a particles' x and y coordinates, respectively. A starting and goal coordinates are respectively Xs, Ys and Xt, Yt.
Step 3: (Evaluation for a fitness function) A direction for a particle is evaluated at each phase. A evaluation method is used to provide measure for how each particle work in problem domain. In PSO, a particle fitness (p fitness) is determined using two limits (distance between points and travel time) indicated by a particles. Over dwindling distance and time, health will increase. For each particle for a feasible pathway, a fitness function is a miniaturization problem and is evaluate d as follows:
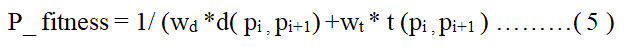
where wd and wt measure a distance and travel time factor respectively, d(pi,pi+1)
denotes a euclidean distance from point Pi to a next point pi+1 for a same particle and t(pi,pi+1) denote time taken to cover a particle from pi to pi+1 as:
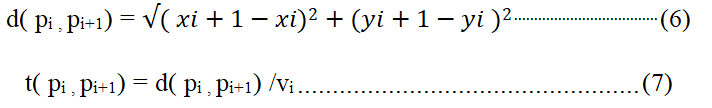
where: xi and yi are an actual horizontal and vertical positions for a particles xi+1 and yi+1 are a next horizontal and vertical positions for a particles and denotes a particle's velocity while moving from pi to pi+1.
Stet 4: Particle location and velocity update a PSO algorithm is initialized with a number for article s and an a optimal is checked. A particle's location is determined by a best position visited y itself which is referred to as a best particle “pbest”, and best position all swarm which is referred to global best “gbest”.
AP article updates its position and velocity where a cognitive component (pbestx1) represents a particle's own knowledge for a best solution and a social component (pbesty1) represents a entire swarm's assumption that a best solution is a best solution. vx2 and vy2 are velocity updated particles. vx1, vy2 and x1, y1 are velocity current particle’s and position along x and y-direction correspondingly. Updating speeds is a way a particle can check for its individual best position and best global location. Factor for self-confidence, c1 and swarm confidence, c2 lets particles behave as a self-summary and learn to a best for a swarm, and get close to a best place for air own and within a swarm, generally c1 equals c2 are ranges from 0 to 4. A inertia weight (w) was first introduced by Eberhart. This concept serves as a recollection for previous speeds and used to monitor a effect for a previous speed on a current speed. A value for inertia factor (w) is within a range for (0, 1). r1 and r 2 are random digits inside (0, 1). Ase parameters have considerable effects on PSO.
Step 5: Generation for feasible paths as particles travel from a current position to a new position through a search location, a conditional statement is used to test all particle paths to see where particles pass through obstacles. If this condition is valid, a route is deemed not acceptable and an algorithm segment Avoidance Barrier is suggested. If a particle path does not interfere with a obstacle's location, an a path is deemed feasible.
A PSO generated path is a collection for "best" points (including a starting point and destination point). A optimum path is created using a proposed algorithm by a line segment which connects a best global position "gbest" located on a ergonomics networks. If a particle trajectory stops at a limit for an obstacle, it is moved to a position outside a obstacleA next step is to compare a particle fitness value between a current position and a new location for each iteration to decide a best pbest position for each particle an d to assign a particle with a best fitness value as a best gbest globally as shown in Figure 4 for a pso flow chart.
Figure 4: Flow chart for PSO.
Results implementation for PSO in path finding
To confirm the effect swarm size on PSO performance, number of particles take (150). The particle size is chose on the basis of trial and error, because there is no recommendation in the literature regarding the size of the swarm. To study PSO performance, the proposed algorithm is applied to the work environment that illustrated a avoidance obstacle at 50 Iteration to find the optimal path. The best simulation results with numbers of particle (150) for the working environment are obtained in Table 3 (Figures 5-12).
| Area of obstacle | Point x obstacle dynamic | Point y obstacle dynamic | Swarm size | Iteration | Best cost |
|---|---|---|---|---|---|
| R=0.4 | X=1.5 | Y=3 | 150 | 50 | 7.5446 |
| R=0.4 | X=2 | Y=4 | 150 | 50 | 7.5123 |
| R=0.4 | X=3 | Y=4.7 | 150 | 50 | 7.7794 |
| R=0.4 | X=3.5 | Y=5 | 150 | 50 | 7.5081 |
Table 3. The simulation results for the working environment using PSO.
Figure 5: Best path at obstacle dynamic point (1.5, 3).
Figure 6: The best cost at 50 iteration.
Figure 7: Best path at obstacle dynamic point (2, 4).
Figure 8: The best cost at 50 iteration.
Figure 9: Best path at obstacle dynamic point (3, 4.7).
Figure 10: The best cost at 50 iteration.
Figure 11: Best path at obstacle dynamic point (3.5, 5).
Figure 12: The best cost at 50 iteration.
In this paper, the path to the mobile robot is identified using the Particle Swarm Optimization (PSO) algorithm, where it is used to find the optimum path of mobile robot in a barrier-free working environment.
The proposed algorithm PSO algorithm is capable of guiding a robot that moves effectively in a complex environment from the starting point to the target point and finding the optimal (shortest) path without collision with any obstacles in the environment. PSO is introduced to address the issue of inapplicable routes. When the particles' path falls at the obstacle boundary, The PSO algorithm is a good choice because of its velocity of convergence and its power in global search.
[Crossref] [Google Scholar] [PubMed]