e-ISSN:2320-1215 p-ISSN: 2322-0112
e-ISSN:2320-1215 p-ISSN: 2322-0112
1Mathematics Department, Shiraz University, Shiraz, Iran.
2Department of Basic Science, Shiraz University, Shiraz, Iran.
Received date: 15/05/2014; Accepted date: 11/06/2014; Published date: 16/06/2014
Visit for more related articles at Research & Reviews in Pharmacy and Pharmaceutical Sciences
Evaluation of chemotherapy treatment in cancer cells is important because of its damaging side effects. For controlling chemotherapy treatment in cancer cells an accurate and comprehensive mathematical model could be useful. Many mathematical models have been used to show the benefits of immune system on controlling the growth of a tumor and the detrimental effects of chemotherapy on both the tumor cell and the immune cell populations. In this article, we offer a novel mathematical model presented by fractional differential equations. This model will then be used to analyze the bifurcation and stability of the complex dynamics which occur in the local interaction of effector-immune cell and tumor cells in a solid tumor. We will also investigate the optimal control of combined chemo-immunotherapy. We argue that our fractional differential equations model will be superior to its ordinary differential equations counterpart in facilitating understanding of the natural immune interactions to tumor and of the detrimental side-effects which chemotherapy may have on a patient’s immune system.
Mathematical Biology, cancer chemotherapy, and optimal drug control
The response to treatment in a tumor is dependent on many factors; some of these factors included are severity of the tumor, application of the treatment and the ability of patient’s own immune system. Over the past decades, mathematical modeling has been developed to evaluate the growth of a tumor and predict the treatment processing. These models can facilitate to control a tumor by predicting its size. In addition, it is possible to evaluate the effect of the body’s natural immune system on tumor cells by these models. They can also help to determine optimal drug treatments or the timing of surgery (e.g., cf. [4-21] and the references therein). After the implicit understanding that chemotherapy has damaging side effects, variety of models have been applied in cancer growth with chemotherapy, these models have been investigated to minimize the total amount of drugs which are used in chemotherapy (See for example [1], [2] and references therein).
In the tumor growth model presented by Pillis [4], an explicit representation of the immune system is included, as well as chemotherapy treatment. This allows not only to incorporate the beneficial effects of the immune system on controlling the growing tumor, but also to track directly the detrimental effects of chemotherapy on both the tumor cell and the immune cell populations. The count of circulating lymphocytes in a patient’s bloodstream is a common clinical practice which is used to reflect the strength of the patient’s overall immune health.
It is understood that this procedure does not provide a complete profile of the patient’s immune health but, it is accepted as one measure. Therefore, in this model two immune components are included: effector-immune cells and circulating lymphocytes. The effector immune cells actively target and destroy tumor cells, while, as stated, the circulating lymphocytes serve as a way to monitor the additional damaging side-effects of chemotherapy [4].
Ordinary differential equations (ODE) and partial differential equations in the form of heat diffusion and statistical equations are just some of the mathematical tools that have been used in deriving these models. In this article, we extend the ODE system presented by de Pillis et al. [4] with using a fractional differential equation (FDE). By using this model we will be able to investigate the optimal control on combination of chemo-immunotherapy. We claim that our FDE model will be better than its ODE counterpart, who facilitates to understand the response of natural immune interactions in a tumor and also it helps to identify the possible damaging side-effects of chemotherapy on a patient’s immune system. Indeed, some of the advantages of our FDE model over previous ones are represented as following. First of all, as it is explained by Andrew Einstein [22], some of the cells in various body organs, for example, breast cells, have a rugged surface. Using ordinary calculus cannot be properly understood because of this nature of the cells. Although, study these cells using fractional calculus may be amenable. In another words, there are some busted points in the surface of these cells where the ordinary (classical) derivative can’t explain them. In this kind of domains, fractional differentiation can be used because, the smoothness property of the domain which is necessary for classical derivatives may not be essential in fractional derivatives. Second, in the definition of the classical derivative of a function only two points in the neighborhood of a point is used. In the definition of the fractional derivative all the points in a neighborhood of a point are used. In this case, more accurate results are obtained in subsequent applications because of using all the accessible information. Non-local property is the term used for this situation which closely reflects reality, and this is primary reason that explains why FDE is increasingly applied to dynamical systems.
In this article, for the circulating lymphocyte population which shows the patient health, we will introduce a FDE model. In this model, the interaction of tumor cell and effector-immune populations in tumor latency is inserted into circulating lymphocyte population which shows a combined FDA model. Moreover, to discuss the dynamical behavior of this model the fixed point and their stability characteristics are determined. We will use Grunwald-Letnikov discretization method to find the solution of this FDE system [23,24], then we will find the results by using software tools such as MATLAB™. Note that chemotherapy is not considered in this FDE model. In the second model in the form of FDE, chemotherapy drug concentration is added to the tumor-immune interactions and we will consider the same three cells populations as in the first FDE. Now, similar to the way in which it can be done in classical ODE systems, we will discuss the dynamic behavior of the system and determine the stability of the various feasible fixed points. One of the main goals in using fractional order instead of classical integer order derivative in our model is to obtain more accurate results in optimally control application of chemotherapy and to minimize the total tumor while constraining the immune state to stay above a specified threshold. For this optimality, similar to linear optimal control method used by de Pillis et al. [4], we will also use it for our FDE model. Obviously, in the processing of this optimality we need to solve our FDE system numerically. To facilitate this solution, as in above first FDE system, we will apply Grunwald-Letnikov method to discretize the model and then use MATLAB™ software to find the results.
As we stated before, we will expect more accurate results in solving our FDE systems as compared to the results found by classical ODE methods.
The first model that we have considered in this section is a three cells population model describing the interaction between the tumor cell (T) plus the effector-immune cell (N) with the circulation lymphocyte population (C), which measures the patient health. If we suppose these three cells evolve with independent variable time, then we can present our model in the form of FDE as follows:
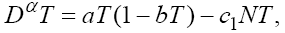
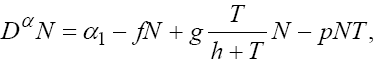 (1)
(1)
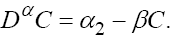
This model is similar to the classical ODE models presented by de Pillis and Radunskaya [17] and de Pillis et al. [4]. Here, we use the same order derivatives 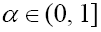 for all three equations with given positive initial values T(0) = T0 N(0) = N0 and C(0) = C0 . Before any justification of these three equations, we should clarify the definition of fractional derivative,
for all three equations with given positive initial values T(0) = T0 N(0) = N0 and C(0) = C0 . Before any justification of these three equations, we should clarify the definition of fractional derivative, 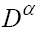 , which is used here. Following the Caputo’s definition for FDE [23], this derivative is defined by
, which is used here. Following the Caputo’s definition for FDE [23], this derivative is defined by 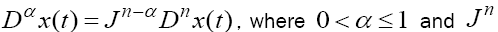 is the nth -order Riemann–Liouville integral operator defined by
is the nth -order Riemann–Liouville integral operator defined by
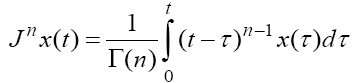
with t = 0 and 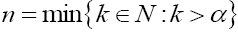 which is one for 0 <α ≤1. Therefore, as we stated above, for the fractional derivative order 0 <α ≤1 the smoothness property of the domain is not essential in this fractional derivative.
which is one for 0 <α ≤1. Therefore, as we stated above, for the fractional derivative order 0 <α ≤1 the smoothness property of the domain is not essential in this fractional derivative.
Here, we have summarized the explanations of three equations in model (1) as follows. In the first equation, the tumor cell population is assumed to grow logistically, while tumor cells are killed by the immune cells through a mass-action dynamic [18]. In the second equation, the immune cells have a constant source rate α1 , while death is proportional to the population of immune cells through the term - fN . Immune cells are also recruited by tumor cells through a Kuznetsov term, g(T /(h+T))N which serves to provide a saturation effect [25]. Additionally, immune cells are inactivated through contact with tumor cells according to a mass-action dynamic. The immune-tumour cell complex of the third equation has a constant source rate α2 and a proportional death term βC . Here, all of the parameters are similar to those presented in [18] so that we can compare our results with those found by other classical ODE models. These values are given in Table 1. These parameters were chosen to be within ranges that are allowed for reasonable dynamics as well as convergence of the optimal control algorithm.
Similar to the classical ODE systems, we can analyze the dynamical behavior of system (1) and determine the stability of its various feasible fixed points. Hence, we first find the fixed points of this system. To find this, from the last equation in (1) we obtain 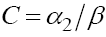 , and from the first equation we get
, and from the first equation we get 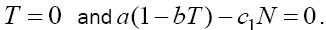 Now, from the second equation with T = 0 we find
Now, from the second equation with T = 0 we find 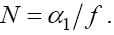
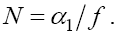 Therefore, one of the feasible fixed points will be
Therefore, one of the feasible fixed points will be 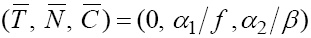 . By calculating the Jacobian of the system we have
. By calculating the Jacobian of the system we have
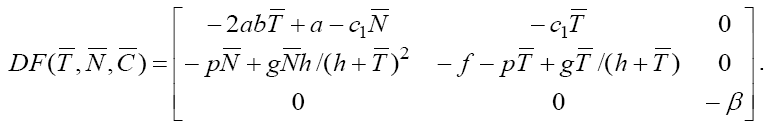
Evaluating the eigenvalues of this Jacobian matrix at evaluated fixed point yields 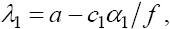
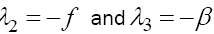 . Obviously, with the parameter values given in Table 1, λ2 and λ3 are negative but
. Obviously, with the parameter values given in Table 1, λ2 and λ3 are negative but 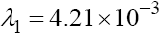 is positive which means this fixed point, with T = 0, is unstable.
is positive which means this fixed point, with T = 0, is unstable.
Now, for the second fixed point with 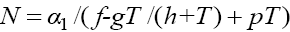 , from the first equation in (1) we get
, from the first equation in (1) we get 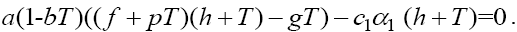 Plugging the parameter values from Table 1 into this third degree equation and solving it by MATLAB™, yields three solutions on which just one of them is positive and acceptable, and the other two are negative which is physiologically unacceptable. With this acceptable positive value of T we will get two other related components of the second fixed point
Plugging the parameter values from Table 1 into this third degree equation and solving it by MATLAB™, yields three solutions on which just one of them is positive and acceptable, and the other two are negative which is physiologically unacceptable. With this acceptable positive value of T we will get two other related components of the second fixed point 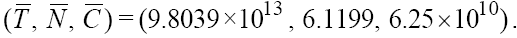 The above Jacobian matrix at this point has three negative eigenvalues λ1 = -0.004324 , λ2 = -1960.809617 and λ3 = -0.0012 . Consequently, system (1) has two fixed points on which the first one with T = 0 is unstable and the second one with a large value of T is stable.
The above Jacobian matrix at this point has three negative eigenvalues λ1 = -0.004324 , λ2 = -1960.809617 and λ3 = -0.0012 . Consequently, system (1) has two fixed points on which the first one with T = 0 is unstable and the second one with a large value of T is stable.
Therefore, in the absence of medical treatment with T0 > 0 the tumor cell populations will grow up to its maximum possible value. At this point, the tumor needed to be controlled by treatment. If we do not control the tumor, the effector-immune cells are not able to renovate. The right hand side in the second equation of system (1) has negative derivative which proofs this fact that while the tumor cell is growing up the effect of the body immune system is converging to zero. This circumstance is also illustrated, as the results of numerical solutions to the system (1), in the next section.
Discretization and Numerical Solutions of FDE Model
As we discussed above, linear stability analysis of system (1) was similar to that of its ODE counterpart. However, to solve FDE system (1) first we need to discretize it. Among the several discretization methods that are available for the fractional derivative 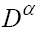 , we have used the one that is granted by Grünwald-Letnikov [23,24]. In this method
, we have used the one that is granted by Grünwald-Letnikov [23,24]. In this method 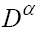 x(t) is approximated by
x(t) is approximated by
Here, l is the step size and [t] denotes the integer part of t . Under this discretization method 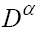 x(t) in system (1) can be replaced by
x(t) in system (1) can be replaced by 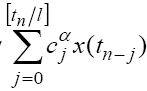 , where
, where 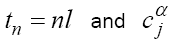 are the Grünwald-Letnikov coefficients which is defined by:
are the Grünwald-Letnikov coefficients which is defined by:
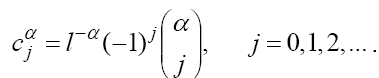
These coefficients can also be evaluated recursively as:
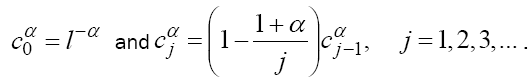 (3)
(3)
Using formula (2), system (1) is discretized as follows:
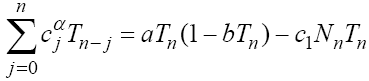
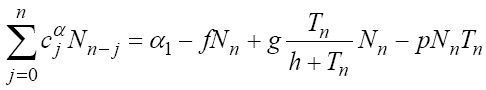 (4)
(4)
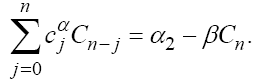
Simple calculation on (4) yields the following recursive formulas:
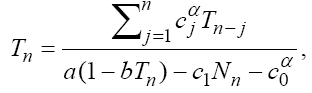
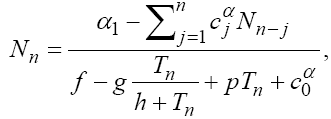 (5)
(5)
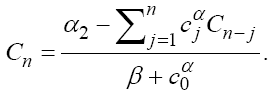
We have used MATLAB™ software to solve this discretized system (5) with initial values 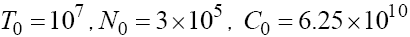 and the results are illustrated in Figures 2-4. In these figures, we consider different values of fractional order derivative 0.90 <α ≤1. As we can see, the normalized values of tumor cells will grow up to its maximum capacity within the long range of time, while the population of natural effector-immune cells is converging to zero. Note that the values of circulation lymphocytes remain without change with respect to the time. As we discussed analytically, these behaviors show the instability of any fixed point of the system with T = 0.
and the results are illustrated in Figures 2-4. In these figures, we consider different values of fractional order derivative 0.90 <α ≤1. As we can see, the normalized values of tumor cells will grow up to its maximum capacity within the long range of time, while the population of natural effector-immune cells is converging to zero. Note that the values of circulation lymphocytes remain without change with respect to the time. As we discussed analytically, these behaviors show the instability of any fixed point of the system with T = 0.
It is clear from Figures 2-4 that the decreasing and increasing rates of T and N , respectively, are slighter while the value of α will be closer to 0.90. Comparing to the results for classical order,α =1 (Figure 2), we claim that these rates are more consistent with the natural reaction of the body immune system. The main reason is the non-local property of FDE. The effect of this property to the results is clear from the discretized system (1) in recursive formulas (5) (look at the summations in the top of the fractions) on which, for the calculation of each unknown valuables in nth point, we have used all possible carrying information by the previous points from j =1 to j = n -1. Hence, the numerical results of system (5) are more accurate comparing to those found by classical ODE counterparts [4,17].
In the next section we will consider three cells population model, as system (1), together with the effect of chemotherapy presented by a system of FDE.
FDE Model with Chemotherapy Treatment
In this section, we consider the same system (1) with three cells population model along with a chemotherapy treatment describing the growth, death, and interactions of each cells. We can present such a system in the form of FDE as follows:
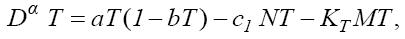
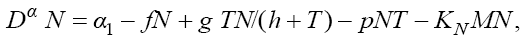
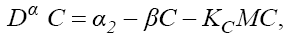 (6)
(6)
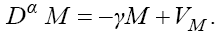
In this model, from the first to the third equations, the effect of chemotherapy to the three cells are shown by the terms consisting of the multiplication of each cell to the drug concentration M with the constant rates KT , KN and KC , respectively. These constant rates are given in Table 1. The variation of drug concentration is shown by the forth equation with an outside treatment source,VM , and the term -M that shows the drug decays out of the system.
To understand the dynamic of system (6), similar to the system (1), we will first find the fixed points and then analyze their stability types. Noting that the fixed points can be evaluated by replacing the left hand side of equations in system (6) to the zero, from the fourth equation we get 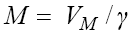 and from the third equation we get
and from the third equation we get 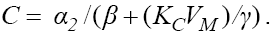 Combining these two we get
Combining these two we get  From the first equation of (6) we get T = 0 and
From the first equation of (6) we get T = 0 and 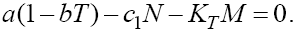 Now, by replacing T = 0 in the second equation we find
Now, by replacing T = 0 in the second equation we find  Hence, one of the fixed points will be
Hence, one of the fixed points will be 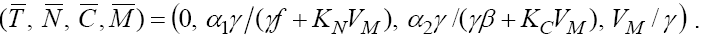 For analyzing the stability of this fixed point, we should find the eigenvalues of Jacobian matrix, but
For analyzing the stability of this fixed point, we should find the eigenvalues of Jacobian matrix, but 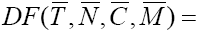
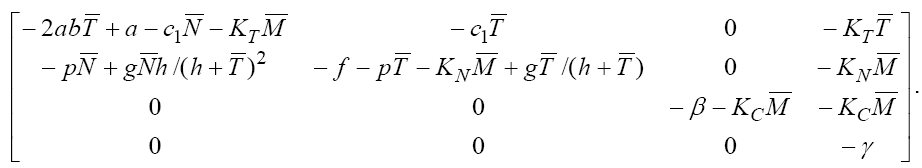 (7)
(7)
Calculating the eigenvalues of this Jacobian matrix at this fixed point, we get 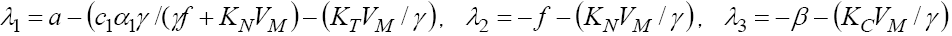 and
and 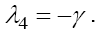 Since all parameters exist in these eigenvalues are positive, the signs of
Since all parameters exist in these eigenvalues are positive, the signs of 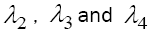 are negative, but the sign of λ1 depend upon the value of VM . We have discussed the case of no treatment,
are negative, but the sign of λ1 depend upon the value of VM . We have discussed the case of no treatment, 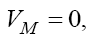 in last section. However, for the case
in last section. However, for the case 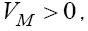 for example for the value
for example for the value 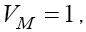 the fixed point will be
the fixed point will be 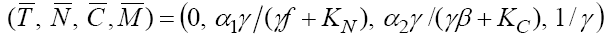 with all negative eigenvalues. This means that if we apply the drug to the system continually, then the fixed point with T = 0 will remain stable. Obviously, the case T = 0 with the existence of positive treatment source cannot be an interesting case. On the other hand, evaluating the other fixed point with non-zero tumor cells population and
with all negative eigenvalues. This means that if we apply the drug to the system continually, then the fixed point with T = 0 will remain stable. Obviously, the case T = 0 with the existence of positive treatment source cannot be an interesting case. On the other hand, evaluating the other fixed point with non-zero tumor cells population and 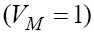 cannot be an interesting case. On the other hand, evaluating the other fixed point with non-zero tumor cells population and
cannot be an interesting case. On the other hand, evaluating the other fixed point with non-zero tumor cells population and 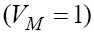 we will get negative values which is biologically unacceptable. So, in order to find the best values for VM on which the tumor cell populations is decreasing down to zero, while the effector-immune and circulation lymphocyte cell populations are increasing to their possible maximum values, we need to apply an optimal control. In this case, in next section we will apply the linear optimal control to the system (6).
we will get negative values which is biologically unacceptable. So, in order to find the best values for VM on which the tumor cell populations is decreasing down to zero, while the effector-immune and circulation lymphocyte cell populations are increasing to their possible maximum values, we need to apply an optimal control. In this case, in next section we will apply the linear optimal control to the system (6).
Linear Optimal Control on Chemotherapy Treatment
In this optimal control, we are minimizing the value of VM subject to the equations of system (6). That is,
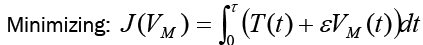 (8)
(8)
Subject to: Four FDE in system (6).
To solve this optimization problem, first we need to clarify the existence of the solutions. To do this, we follow the same arguments that have been done by De Pillis and Radunskaya in [17] and the results from Fleming and Rishel in [26]. We should just note that here in system (6); we are dealing with fractional derivatives while the derivatives in the above referred articles are just the ordinary derivatives. However, in fractional derivative, since the properties that exist for α =1 are also satisfied for any 0 <α<1, there is no difference between the optimal control theorems in both cases.
Now, for the existence solution of (8), first we note that the solutions are bounded with respect to the finite time. This is clear, since the following sub system of (6) has bounded solutions.
Therefore, acceptable (positive) solutions of system (6) are bounded from above. Next, we state the existence solution theorem for optimal problem (8) without the proof [18,26].
Theorem 1 Optimization problem (8) has a solution 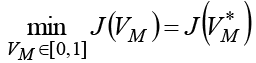 in admissible control
in admissible control 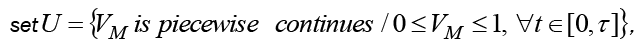 with some initial value T(0) = T0, N(0) = N0, C(0) = C0 andM(0) = M0 , if the following conditions are satisfied.
with some initial value T(0) = T0, N(0) = N0, C(0) = C0 andM(0) = M0 , if the following conditions are satisfied.
First, the set U should be nonempty, closed and bounded. Second, right hand side functions in system (6) are all continues, bounded above by a sum of the bounded control and the state, and can be written as a linear function of VM with some coefficients depending on time and the state. And third, the integrand of J (VM ) is convex on U and is bounded below by some linear combination of 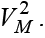
Now, we are ready to state the characterization of linear optimal control theorem, with the proof, using Pontryagin’s Maximum Principle [27].
Theorem 2 Suppose an optimal control 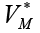 and the solutions of system (6) that minimize the function
and the solutions of system (6) that minimize the function 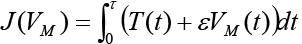 are given. Then there exist adjoin variables
are given. Then there exist adjoin variables 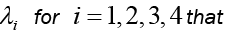 satisfy to the following system
satisfy to the following system
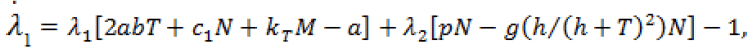
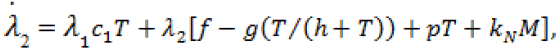
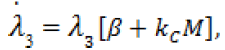 (9)
(9)
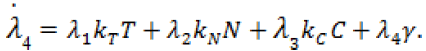
Here, 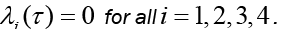 Moreover, the optimal
Moreover, the optimal 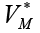 is given by
is given by

Where
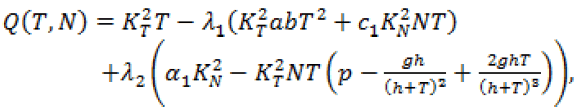 (10)
(10)
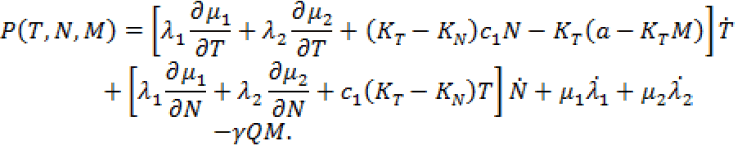 (11)
(11)
In this case, the Hamiltonian of the system is given by
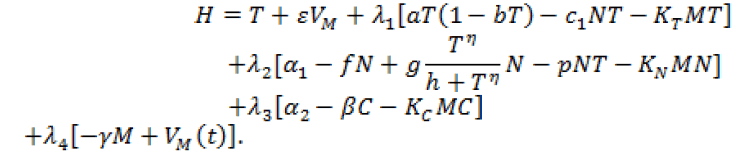 (12)
(12)
The switching function in this case is 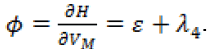 Since there is no explicit dependence on
Since there is no explicit dependence on 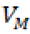 in the switching function, the possibility of singular arcs arises. The optimal control is given by
in the switching function, the possibility of singular arcs arises. The optimal control is given by

In the regions where the switching function is not zero, we have bang-bang control. In order to address the issue of singular arcs, we suppose the switching function is zero on an interval 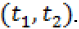 . This implies that all the derivatives of
. This implies that all the derivatives of 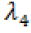 must vanish in that interval. We can use this fact to determine the optimal control in such regions.
must vanish in that interval. We can use this fact to determine the optimal control in such regions.
For the explanation to follow, we recall that 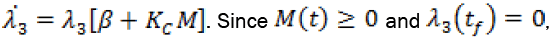 we can conclude that
we can conclude that 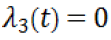 on the entire time interval. Setting the first three time derivatives of the switching function to zero, and using
on the entire time interval. Setting the first three time derivatives of the switching function to zero, and using  , we obtain
, we obtain
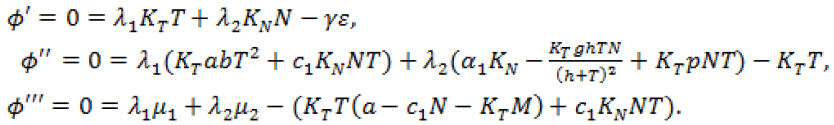 (13)
(13)
Where
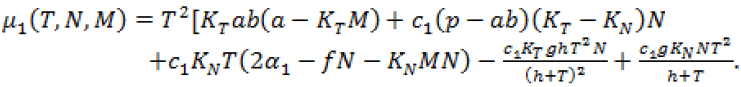 (14)
(14)
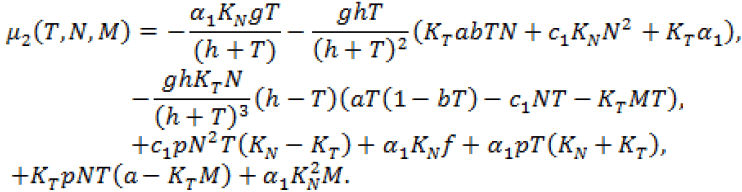 (15)
(15)
From  we can solve for
we can solve for 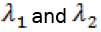 in terms of the state. We get
in terms of the state. We get
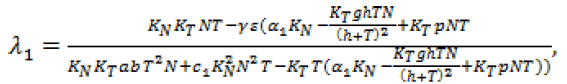 (16)
(16)
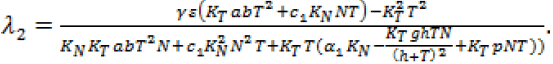 (17)
(17)
Now, we know all four adjoin variables in terms of the state in a singular region. To determine the control, we need to find the fourth derivative of the switching function. We then get a linear equation in 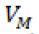 whose coefficients are functions of T, N and M. We see that
whose coefficients are functions of T, N and M. We see that 
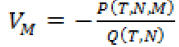
Where
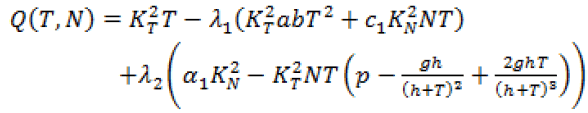 (18)
(18)
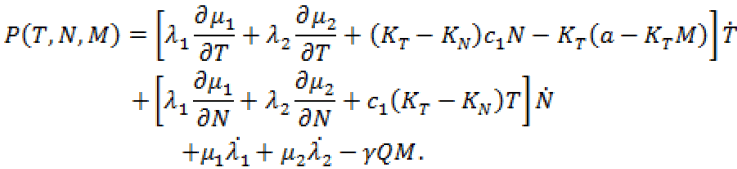 (19)
(19)
Here, 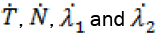 are given by the relevant expressions for the time derivative in the state and adjoin equations and
are given by the relevant expressions for the time derivative in the state and adjoin equations and
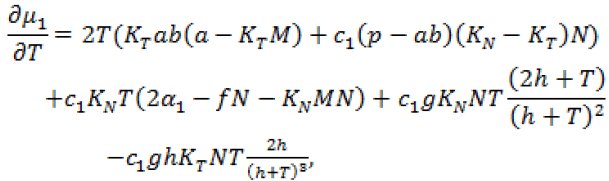 (20)
(20)
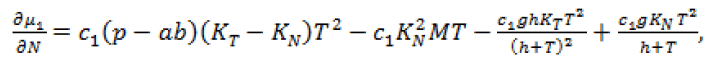 (21)
(21)
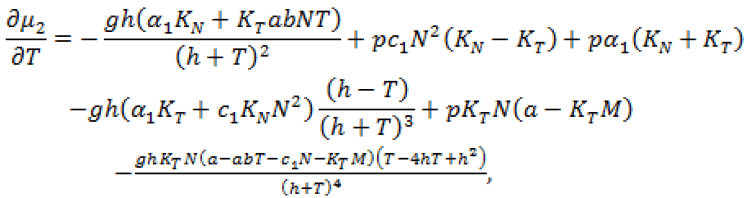 (22)
(22)
and
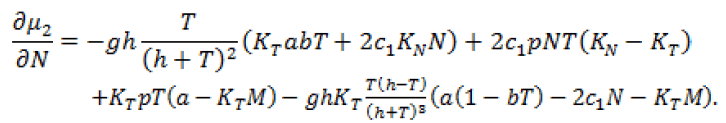
Since, we know 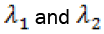 in terms of the state variables T and N, we know Q purely in terms of T and N. For the singular control to be minimizing the Generalized Legendre Clebsch condition needs to be satisfied, that is Q (T, N) would have to be non-negative on this interval [4]. The results are shown in Figure 5. Note that Q (T, N) is only negative in a very specific region. In this region, we can guarantee that there are no singular minimizing arcs, so the control is bang-bang. In other regions, the potential for singular arcs has not been ruled out, but in fact arises in most practical situations, since most of the T-N plane meets the criterion Q(T,N) ≥ 0 [4].
in terms of the state variables T and N, we know Q purely in terms of T and N. For the singular control to be minimizing the Generalized Legendre Clebsch condition needs to be satisfied, that is Q (T, N) would have to be non-negative on this interval [4]. The results are shown in Figure 5. Note that Q (T, N) is only negative in a very specific region. In this region, we can guarantee that there are no singular minimizing arcs, so the control is bang-bang. In other regions, the potential for singular arcs has not been ruled out, but in fact arises in most practical situations, since most of the T-N plane meets the criterion Q(T,N) ≥ 0 [4].
In writing system (9) we may consider the columns of Jacobian matrix (7). Now for solving optimization problem (8), we should first solve system (9) with some values of T,N,C and M . Here, to be consistent with other results in [4,17], we start with 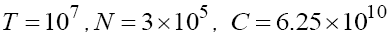 and M = 0 . Then, by finding the value
and M = 0 . Then, by finding the value 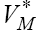 and plugging into the system (6), instead of VM , we are ready to solve this system with the same starting point T,N,C andM as above. The similar discretization method that we have done for FDE system (1) can be applied here for system (6) to get
and plugging into the system (6), instead of VM , we are ready to solve this system with the same starting point T,N,C andM as above. The similar discretization method that we have done for FDE system (1) can be applied here for system (6) to get
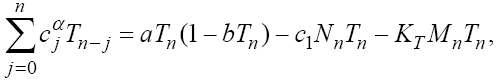
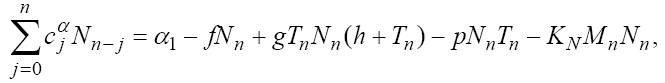
 (24)
(24)
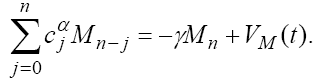
Now, by simple calculation on (24), we get the following recursive formula.
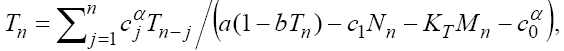
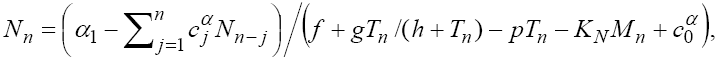 (25)
(25)
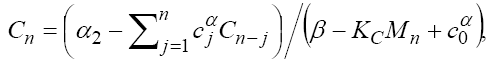
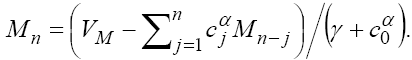
By solving this system for some customary time, say t  [0,9] , we arrive at the new point with a new set of values T , N , C and M . Then, this new set of values will serve as a new starting point with initial values
[0,9] , we arrive at the new point with a new set of values T , N , C and M . Then, this new set of values will serve as a new starting point with initial values 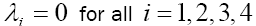 for solving system (9), in the next iteration, to find a new optimal value of
for solving system (9), in the next iteration, to find a new optimal value of  These iterations will continue up to the time t =100 (days). Indeed, using MATLAB™ to solve these two joint systems (9 and 11), as the solution of optimal problem (8), the results are illustrated in Figures 6- 11 for different values of fractional derivative 0.90 <α <1. Figure 6 represents the results for Α = 1. In this figure, the results are in complete agreement with those found by using the classical systems of ODE counterparts [4,17]. However, in Figures 7 and 8 the results for the values 0.90 <α <1 are somehow different from Figure 6. We claim that these results are in more agreement with the nature of the chemotherapy treatment. The amount of the medicine that has been used in each period of time (each 9 days) is completely visible at the starting iterations, and shows a oscillatory pattern that is converging to zero in a long range of time. Almost the same pattern can be seen for the tumor cell populations. This oscillatory pattern is more visible in Figures 10 and 11, and also shows the amount of controlled medicine in each period of time (each 9 days) for α = 0.98 and 0.95, respectively. On the other hand, in Figure 9 which demonstrates evaluated optimal values of
These iterations will continue up to the time t =100 (days). Indeed, using MATLAB™ to solve these two joint systems (9 and 11), as the solution of optimal problem (8), the results are illustrated in Figures 6- 11 for different values of fractional derivative 0.90 <α <1. Figure 6 represents the results for Α = 1. In this figure, the results are in complete agreement with those found by using the classical systems of ODE counterparts [4,17]. However, in Figures 7 and 8 the results for the values 0.90 <α <1 are somehow different from Figure 6. We claim that these results are in more agreement with the nature of the chemotherapy treatment. The amount of the medicine that has been used in each period of time (each 9 days) is completely visible at the starting iterations, and shows a oscillatory pattern that is converging to zero in a long range of time. Almost the same pattern can be seen for the tumor cell populations. This oscillatory pattern is more visible in Figures 10 and 11, and also shows the amount of controlled medicine in each period of time (each 9 days) for α = 0.98 and 0.95, respectively. On the other hand, in Figure 9 which demonstrates evaluated optimal values of 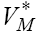 for α =1in different periods of time, no such oscillatory pattern can be seen. We can have similar discussion for decreasing pattern of natural effectorimmune and circulation lymphocyte cell populations in Figures 6-8. We emphasize that the reason for the accuracy of FDE is the non-local property of these equations. This means that the next state of a system not only depends upon its current state but also upon its historical states starting from the initial time. To see this, pay attention to the summation terms in the right hand side of system (25).
for α =1in different periods of time, no such oscillatory pattern can be seen. We can have similar discussion for decreasing pattern of natural effectorimmune and circulation lymphocyte cell populations in Figures 6-8. We emphasize that the reason for the accuracy of FDE is the non-local property of these equations. This means that the next state of a system not only depends upon its current state but also upon its historical states starting from the initial time. To see this, pay attention to the summation terms in the right hand side of system (25).
In this article, we introduced a three cells population model describing the interaction between the tumor and the effector-immune cells together with the circulation lymphocyte population, without any treatment, in the form of FDE. As we have seen, the local stability analyses of the fixed points for this FDE system were the same as its counterpart ODE system. These analyses were agreed with numerical results of discretized FDE system using Grünwald-Letnikov method. As we have expected the tumor cell population were increasing up to its maximum values by any positive initial value. Hence, a more reliable FDE system with chemotherapy treatment was considered. In order to find the best amount of medicine on which the tumor cell population is decreasing, while other two variables, the effector-immune cells and circulation lymphocyte population are increasing, we conducted a linear optimal control. We could adapt the same existence and characteristic optimal control theorems as in ODE systems for our FDE system. We claim that due to the non-local property of FDE, the results found by this system were more accurate as we compare to the results found by counterpart ODE models. We also claimed that the results would be more accurate when we use the lower value of α in the interval (0.9,1] . However, we should note that by choosing any smaller values α , we will encounter a larger amount of errors in calculations. In these two FDE systems that we have introduced here, experimentally, we have found that the best value of α for the best results is 0.95.