International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Economic Load Dispatch Using AI Technique

Charanjeet Madan1, Bhuvnesh Khokhar1 and Rohini Sharma2
  1. Assistant Professor, Dept. Of EE, Hindu College of Engineering, Sonipat, India
  2. M.Tech scholar, Dept. of EE, Hindu College of Engineering, Sonipat, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper, anti-predatory particle swarm optimization (APSO) technique has been used for solving the economic dispatch (ED) problems. The feasibility of the proposed algorithm is applied to three generator & six generator thermal power plants. The performance of APSO has been compared to the classical particle swarm optimization (SPSO) strategy, a new version of the classical particle swarm optimization namely, new PSO (NPSO), and Genetic algorithm (GA). Effect of valve-point loading (VPL) has been considered for the three generator system whereas this effect has been omitted for the six generator system. Comparison results show that the APSO provides better solutions and more stable convergence characteristics as compared to the other techniques.

Keywords
Anti-predatory particle swarm optimization (APSO), Economic dispatch (ED), Genetic algorithm (GA), Valve point loading (VPL)

INTRODUCTION
One of the substantial operating tasks in power system is to reduce the total generation cost. The fundamental issue in modern power system operation is the ED. It is a crucial optimization problem and its main objective is to divide the required power demand among online generators. It is used to minimize the generation cost of units, with satisfaction of equality and inequality constraints [1, 2]. An optimization process saves significant amount of money. In the past decades, certain conventional optimization techniques have been applied effectively for monotonically increasing piece-wise linear function such as lambda iteration method, Newton-Raphson method, and linear programming [1, 5-6]. A practical ED problem must consider prohibited operating zones, valve point effects to provide the completeness for the ED formulation. For solving the non-linear cost functions, some artificial intelligence (AI) techniques such as artificial neural network (ANN) [7], Genetic algorithm (GA) [6, 8-9] have been applied in the past.
Artificial neural networks suffer from huge calculations due to excessive numerical iterations. Walters and Sheble [6] presented a GA algorithm solution of ED including valve point effects [6]. Also Chen and Chang [8] presented an algorithm that included network losses and valve-point effects. Although, the GA model has been employed in various optimization problems, recent researchers have identified some deficiencies in its performance such as slow convergence near global optimum [12]. Premature convergence is another issue that reduces its searching capability [11].
PSO was developed by Kennedy and Eberhart in 1995 motivated by social behaviour of organisms such as fish schooling and bird flocking [1]. It is a meta-heuristic algorithm for solving the non-linear and non-continuous optimization problems [13, 18].The central idea of the classical PSO relies on the foraging activity of the swarm. Both the cognitive and social behaviour are the constituents of the foraging activity. PSO generates high quality solutions with less calculation time and faster convergence as compared to the other AI techniques [11, 13-14]. Unlike in GA, its velocity of particle is updated according to its previous best position of its companions [13]. PSO rapidly finds a good local solution but get stuck to it for the rest of iterations [15, 17]. In this paper, APSO has been successfully employed to overcome the above problems. APSO is modified by splitting into cognitive and social behaviour of classical PSO and hence premature convergence is avoided. The experimental results are compared with SPSO [18], NPSO [19]. Two test systems have been taken for the performance comparison. The first test system consists of three generating units [6] whereas the second test system comprises six generating units [13].

PROBLEM FORMULATION
ED is one of the key functions in electrical power system operations. Practically, the ED must perform the optimal generation dispatch among the operating units to satisfy the load demand, spinning reserve capacity, and practical operation constraints of generators. The proposed formulation including valve point loading effect (EDVPL) has been modeled in a recurring rectified sinusoidal function [1].The objective of the ED problem is to minimize the total fuel cost. Mathematically, ED problem considering VPL [1] is defined as:
image

REVISION OF VARIOUS PSO STRATEGIES
Various PSO based strategies have been applied to solve the EDVPL problem. In proposed paper, some of PSO strategies are discussed and their experimental results compared with APSO strategy.
A. Classical PSO (SPSO)
SPSO is fast calculation technique, help to solve the ED problems. It is an optimization tool which provides a population-based search procedure in which individuals denote particles. These particles change their position with respect to time in a multi dimensional search space [1, 18]. Let p and v represent a particle (position) and its corresponding flight speed (velocity) in a search space respectively. The velocity of particle is controlled by three components, namely, inertial, cognitive, and social [19]. The inertial component simulates the inertial behaviour of the bird to fly in the previous direction. The cognitive component models the memory of the bird about its previous best position, and the social component models the memory of the bird about the best position among the particles (interaction inside the swarm). The modified velocity and position of each particle can be calculated using the current velocity and the distance from pbestid to gbestid as shown in the following formulas [1].
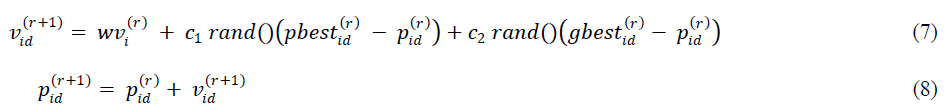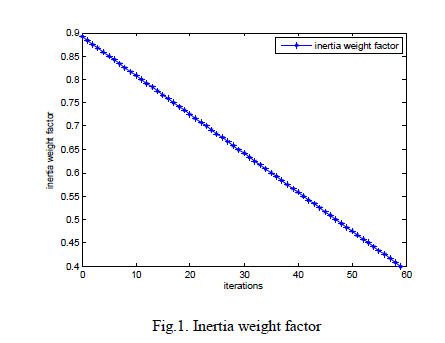image
image
image
Fig. 1 shows the linearly decreasing weight factor which is vary from about 0.9 to 0.4 during a 60 iterations.
B. NEW PSO (NPSO)
A new variation namely NPSO in the classical PSO is updated by splitting the cognitive component into two different components-cognitive and social components [1, 19]. The cognitive and social component denotes good experience and bad experience respectively. That is, the bird has a memory about its previously visited best position of cognitive component. The bad experience component helps the particle to remember its previously visited worst position. To calculate the new velocity, the bad experience of the particle is also taken into consideration. The new velocity update equation is given by [1]
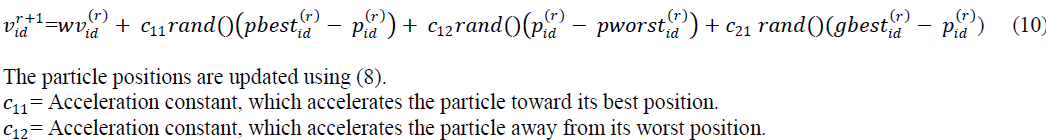image
image

PROPOSED PSO STRATEGY
A. ANTI-PREDATORY PSO (APSO)
APSO [20] strategy has been used to solve the economic dispatch including valve point loading effect (EDVPL) problem efficiently and economically. The main objective is used to enhance the convergence of the particles in later stages. APSO is developed by splitting both component i.e. cognitive and social component. In the original PSO, food location is modeled as the best result points of the optimization problem. APSO considers worst results as predators. APSO is developed by splitting both cognitive and social behaviors optimization. This is done by using the bad experiences, particle always by-passes its previous worst positions. Hence, exploration capability is further improved.
B. APSO PROCEDURE FOR ELD
Steps for optimizing the EDVPL problem using APSO are briefed below:
Step 1: In this paper, we adopt the output of each real power generation unit as a gene. Hence, a number of genes comprise for formulation of the swarm. p is the set of real power output among all the online generators are use to refer the position of the particle in the swarm. For a system with ng generators, Npar particles are considered in swarm. The complete swarm is represented as a matrix as shown below:
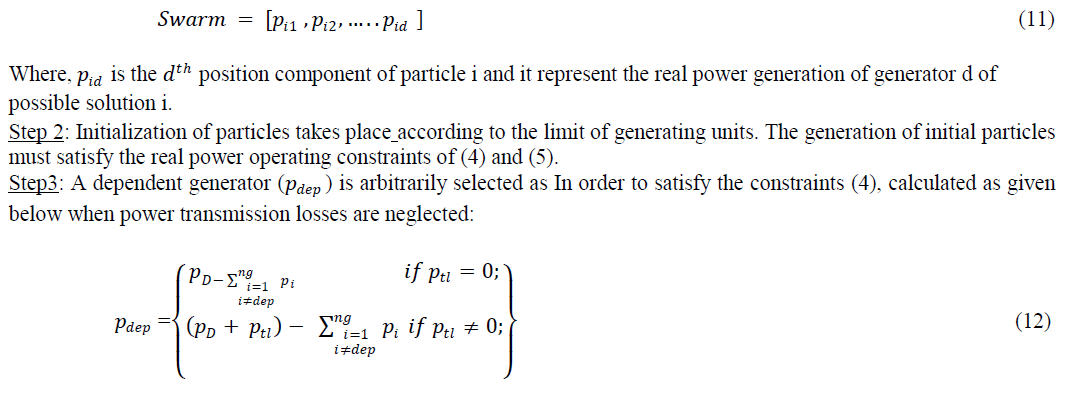image
image
image

TEST SYSTEMS AND RESULTS
In order to show the superior convergence characteristics than the other various PSO strategies, two different test systems have been taken into consideration. The first test system consists of three generator units with a load demand of 850MW [6] whereas the second test system comprises six generator with a load demand of 1263MW [14]. The parameters used for different PSO strategies are shown in table 1.
image
A. CASE 1:THREE GENERATOR SYSTEM
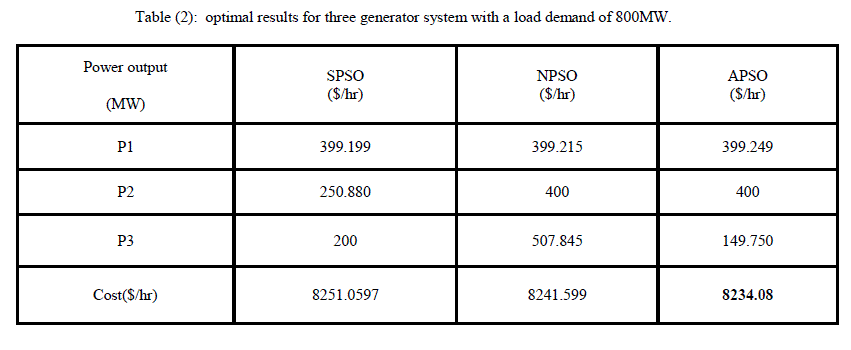
Data for three generator system has been taken from [6] including VPL effect with a load demand of 850MW.Population size of 20 has been taken with a maximum number of iterations as 200. Losses are neglected. Power output of individual generators and generating cost are shown in table (2). Table 2 shows comparison result among all the previously discussed techniques.
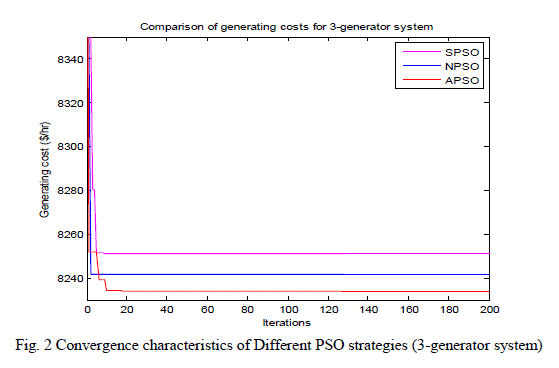image
image
In the fig 2, it shows the Convergence characteristics. It represents the better results obtained through APSO among all applied techniques.
B. CASE 2: THREE GENERATOR SYSTEM
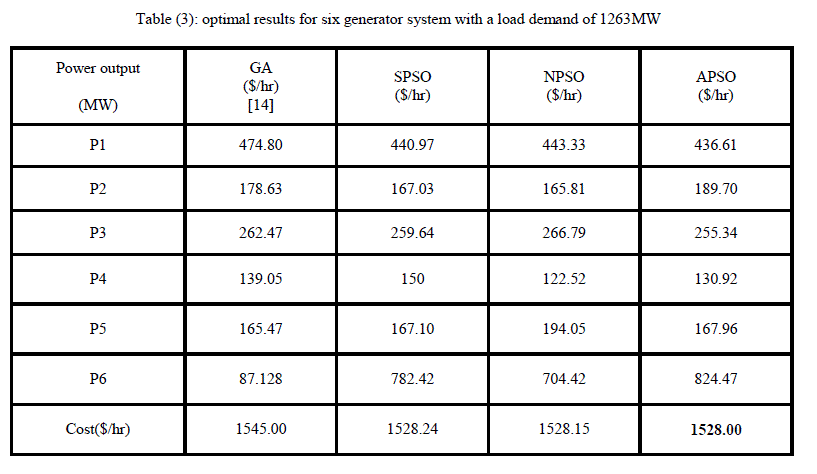
Data for three generator system has been taken from with a load demand of 1263MW [14]. In this case, VPL effect and losses are not considered. Population size of 100 has been taken with a maximum number of iterations as 200. Power output of each generator and generating cost respectively are shown in table (3). Table 3 shows comparison results for all given techniques.
image
image
In Fig 3, Convergence characteristics are shown. . It represents the better results obtained through APSO among all applied techniques.

CONCLUSION
In this paper ASPO is successfully applied to ED problems with and without the valve point loading effect. The results of APSO have been compared with SPSO, NPSO in first case and GA is also included with the six generator system. The results obtained show that APSO outperforms the other PSO strategies particularly for the EDVPL problem in term of solution quality and provides a stable convergence. Also the problem of premature convergence is reduced.

References
  1. D. P. Kothari and J. S. Dhillon, “Power System Optimization”, 2nd edition, PHI, New Delhi, 2010
  2. D. P. Kothari and I. J. Nagrath, “Power System Engineering”, 2nd edition, TMH, New Delhi, 2010
  3. D. P. Kothari and I. J. Nagrath, “Modern Power System Analysis”, 3rd edition, TMH, New Delhi, 2009.
  4. Bakirtzis, V. Petridis, and S. Kazarlis, “Genetic Algorithm solution to the economic dispatch problem”, IEEE proceeding on Gen., Transm. Dist vol. 141, No.4, pp. 377-382, July 1994
  5. K. Mohamed-Nor and A. H. A. Rashid, “Efficient Economic dispatch algorithm for thermal unit commitment”, IEEE Proceedings C, vol. 138 no.3, pp. 213-217, 1991.
  6. D. C.Walters and G. B. Sheble, “Genetic algorithm solution of Economic dispatch with valve point loading”, IEEE1993.
  7. K. Y.Lee,A.Sode-Yome and J. H. Park, “Adaptive Hopfield neural networks for economic load dispatch”, IEEE Trans. on Power Systems, vol. 13, no. 2, pp. 519-526, 1998.
  8. P. C. Chen and H. C. Chang, “Large scale economic dispatch by genetic algorithm”, IEEE Trans. on Power Systems, vol. 10, pp. 1919-1926, 1995.
  9. B.Sheble and K. Brittig,“Redefined genetic algorithm – economic dispatch example”, IEEE Trans. on Power Systems, vol. 10, pp. 117-124, 1995.
  10. C. L. Chiang, “Improved genetic algorithm for power economic dispatch of units with valve point effects and multiple fuels”,IEEE Trans. on Power Systems, vol. 20, no. 4, pp. 1690- 1699, 2005.
  11. R. C. Eberhart and Y. Shi,“Comparison between genetic algorithms and particle swarm optimization,” Proceedings of IEEE Int.Conference on Evolutionary Computation, pp.611–616, May 1998.
  12. M. Sudhakaran, Dr S M R Slochanal,”Integrating Genetic Algorithms and Tabu Search for emission on and Economic Dispatch Prob lems”, IE (I) J ournal –EL, vol 86, pp.39-43, June 2005.
  13. Y. Shi and R. Eberhart, “A modified particle swarm optimizer”,Proceedings of IEEE Int. conference on Evolutionary Computation,pp. 69-73, May 1998.
  14. Z. L.Gaing, “Particle swarm optimization to solve the economic dispatch considering the generator constraints”,IEEE Trans. on Power , vol. 18, no. 3, pp. 1187-1195, 2003.
  15. J.B. Park, K.S. Lee, J.R. Shin and K.Y. Lee, “A particles warm optimization for economic dispatch with non-smooth cost functions” IEEE Trans. on Power Systems, vol. 20, no. 1, pp.34- 42,2005.
  16. A.Ratnaweera, S. K. Halgamuge and H. C.Watson,“Self-organizing hierarchical particle swarm Optimizer with time varying acceleration coefficients”, IEEE Trans. on Evol.Comput., vol. 8, no. 3, pp. 240-255, 2004
  17. T. Arduloss, A. Victoire and A. E. Jeyakumar, “Reserve constrained dynamic dispatch of units with valve point effects”, IEEE Trans. On power Systems, vol. 20, no. 3, pp.1273-1282, 2005.
  18. J. Kennedy and R. Eberhart, “Particle swarm optimization”, Proceedings of IEEE Int. Conf. on Neural Networks, vol. 4, pp. 1942-1948, 1995.
  19. A. I.Selvakumar and K. Thanushkodi, “A new Particle swarm optimization solution to nonconvex economic dispatch Problems”, IEEE Trans. on Power Systems, vol. 22, no. 1, pp. 42-51, 2007.
  20. A. I.Selvakumar and K. Thanushkodi, “Anti-Predatory particle swarm optimization: Solution to nonconvex economic dispatch problems”, Electric Power Systems Research, vol. 78, pp. 2-10, 2008.