e-ISSN: 2320-7949 and p-ISSN: 2322-0090
e-ISSN: 2320-7949 and p-ISSN: 2322-0090
Manlla AM1, Oliva MA2, Lopez GL2,and Lopez ME3*
1Department of Mathematics, Faculty of Agronomy and Zootechnics, National University of Tucuman, Argentina
2Department of Endodontics, School of Dentistry, National University of Tucuman, Argentina
3Department of Biological Chemistry, School of Dentistry, National University of Tucuman, Argentina
Received date: 01/01/2019; Accepted date: 06/02/2019; Published date: 13/02/2019
Visit for more related articles at Research & Reviews: Journal of Dental Sciences
Citric acid is an irrigation solution used in endodontic as a sodium hypochlorite adjuvant since it has a demineralizing action, which facilitates instrumentation in narrow or calcified canals and contributes to the elimination of dentine clay. In a statistical analysis, the response variables are those that best express the effect of the experimental factors on the observation units and can be qualitative or quantitative. The objective of this paper is to present a routine to analyze qualitative variables in R language, from data related to the cleaning of the root canal system with ultrasound and citric acid as an endodontic irrigator. The contingency table was organized with the records of the response variable "Cleaning with citric acid from the root canal system" based on the experimental factor "Exposure to ultrasound". With the frequencies of occurrence of the different categories of the response variable (TA-0: "all open tubules, no mud in the dentin wall", TA-1: "more than 50% of the open tubules", TA-2 : "Less than 50% of open tubules" and TO-3: "all obliterated tubules") registered in both levels of the experimental factor (CU: "with ultrasound" and SU: "without ultrasound"), without discriminating by third observed (AP: "apical", CE: "cervical" and ME: "medium"), proportions were determined as frequencies relative to the general total (all values are comparable) and represented in bar graphs to facilitate the identification of models of cleanliness behaviors in samples exposed and not exposed to ultrasound. Subsequently, hypotheses were formulated regarding the association between the response variable and the experimental factor (level of cleanliness and exposure to ultrasound) and the difference between pairs of proportions (of the samples exposed and not exposed to the experimental factor in the different levels of the variable answer), to be contrasted with the Chi Square or Exact Fisher test and Z for proportions. Finally, the association measures between qualitative variables were calculated, based on the test statistic of the first test. The results of the Fisher Exact test (on the original contingency table) and Chi square (on the modified contingency table so that the categories do not have frequencies less than 5) indicate that the association (p>0.05) between "Cleaning with citric acid" and "Exposure to ultrasound". That is, the differences between the proportions of the samples with and without ultrasound at the different cleaning levels are not significant. This was confirmed with the results of the Z test for proportions since no significant differences were detected in the comparisons made) and with the calculated association measures (the highest value corresponded to the corrected contingency coefficient K=0.153962, which due to its proximity to zero induces to estimate a weak association between the response variable and the experimental factor). Citric acid achieved the level of cleanliness TA-0 in the sample with ultrasound, contrary to another irrigant that achieved the aforementioned cleaning level in the sample without ultrasound.
R Language, Irrigant solutions, Chi square test, Fisher exact test, Z test for proportions, Contingency coefficients
Endodontic irrigators are chemical solutions used for the disinfection and cleaning of the root canal system [1]. Irrigation acts on the dissolution of organic matter and dentinal clay produced by the action of endodontic instruments, also has antiseptic action, contributes to the dragging of the duct waste avoiding apical tamponade and lubricating action avoiding premature wear and fracture the endodontic instruments [2].
The most frequently used irrigation solution is 0.5%-5% sodium hypochlorite [3]. Due to the fact that it has no action on the inorganic component of dentin [4], its use is complemented with demineralizing solutions, among which the Ethylenediaminetetraacetic Acid (EDTA) 17% solution [2]. Acids such as citric acid 1-50% [5], acetic acid or maleic acid 5% are also used.
The ultrasound creates bubbles of positive and negative pressure in the liquid molecules that come into contact with each other, becoming unstable and collapsing. This would cause an implosion similar to a vacuum decompression. Numerous studies compared the effectiveness of ultrasound with respect to manual irrigation in the elimination of debris and cleaning of the root canal, concluding that the cavitation of the irrigant contributes to achieving greater effectiveness of it [6,7].
In a statistical analysis, the response variables are those estimated as those that best express the effect of the experimental factors on the observation units. When the values come from measurements or counts the variables answers can be quantitative whereas when their values come from subjective qualifications, they are qualitative.
The statistical analysis of qualitative response variables implies the classification of the frequencies of occurrence of the experimental categories in contingency tables, the determination of the proportions of occurrence of said categories as frequencies relative to the general total or total rows or total of columns, the visualization of the proportions in bar graphs, the formulation of hypotheses referring to the independence of the response variable with respect to an experimental factor and/or referring to differences between pairs of dubious proportions, the contrast of the hypotheses with the appropriate tests and the determination of complementary measures such as contingency coefficients, difference of proportions and ratio of proportions [8-12].
The "contingency table or cross" is an arrangement that allows summarizing the frequencies of occurrence of experimental events by classifying them according to two or more categorical variables (nominal or ordinal qualitative), facilitating the determination of basic information as relative frequency (proportion or probability) of occurrence of said events, the hypothesis about the association between variables and difference between pairs of proportions, to be contrasted with adequate tests.
To determine the significance of the association between variables recorded in independent samples, the Chi Square test is used, if the absolute frequencies of each category is greater than 5, which in R language is executed with the function "chisq.test (vr, fe) "Or" chisq.test".
If the variables were recorded in paired samples (related or dependent) and organized in a 2x2 table (arrangement for dichotomous variables, such as before or after treatment, if exposed or not exposed, etc.) the McNemar test is used, which R language is executed with the function "mcnemar.test (vr, faith)" or "macnemar.test".
In the circumstances not contemplated by the previous tests, the Exact Fisher test is used, which in R language is executed with the function "fisher.test (vr, fe)" or "fisher.test". In practice, this test is used when the sample sizes are small, but it is valid for all sample sizes.
The functions were presented in their simplest application, but they have alternatives to solve situations of different complexity, which can be seen in the help of the R language.
To intensify the evaluation of qualitative variables one can determine the "relation of proportions" (important for comparing proportions close to zero) and the "contingency coefficients" (measures of the association between qualitative variables based on the "chi square" coefficient that try eliminate the restrictions of the Chi Square test statistic).
The "quadratic or chi-squared contingency coefficient", based on observed (Oij) and estimated (Eij=hi.*Hj./N) assuming total independence, is determined as 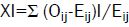
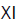 values close to zero indicate independence between the variables (the minimum value occurs when the numerator is zero) and as the value increases, the association between the variables is more intense. The maximum value depends on the dimension of the contingency table and the sample size, it being inappropriate to compare
values close to zero indicate independence between the variables (the minimum value occurs when the numerator is zero) and as the value increases, the association between the variables is more intense. The maximum value depends on the dimension of the contingency table and the sample size, it being inappropriate to compare 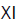 values of different tables in number of events and sample sizes.
values of different tables in number of events and sample sizes.
The "quadratic mean contingency coefficient", which is obtained by dividing the previous coefficient with the sample size 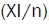 , in the case of a 2x2 table assumes values between zero and one.
, in the case of a 2x2 table assumes values between zero and one.
The "contingency coefficient C or CC or K of Pearson" tries to eliminate the restriction of the size of the sample with the expression 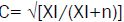 . The upper limit is obtained with the expression
. The upper limit is obtained with the expression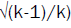 , with "k" being the minimum number of categories of the variables studied.
, with "k" being the minimum number of categories of the variables studied.
The "corrected contingency coefficient K", which is obtained with the expression K=C*√(k/k-1), by eliminating the influence of the dimension of the tables on the upper limit makes the results comparable. Here governs 0 ≤ K ≤ 1, where a K value close to 0 indicates independent variables and close to 1 indicates a greater dependence between the variables.
The "Phi coefficient" measures the association of dichotomous variables (correlation coefficient of 4 fields) with the expression 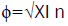 (it is the square root of the mean quadratic coefficient of contingency).
(it is the square root of the mean quadratic coefficient of contingency).
The value of the coefficient oscillates between 0 (indicates absence of association between variables) and infinity (the coefficient is not bounded).
The "Cramer's V coefficient", at least one of the variables is dichotomous and is not restricted by the size of the sample, is obtained with the expression: 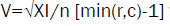 where min (r,c) is the smallest value between the number of rows and the number of columns in the table.
where min (r,c) is the smallest value between the number of rows and the number of columns in the table.
For any dimension of the contingency table, the coefficient V oscillates between 0 and 1. In a 2x2 table, the Cramer V coefficient corresponds to the Phi coefficient.
The "relation of proportions" allows a better evaluation of the difference of unrepresentative proportions (close to 0 or 1), it is obtained by dividing both proportions (r=p1/p2) and is interpreted as the times that is greater or lesser with respect to the other. When the variables are independent, the proportions are similar and the ratio closes to unity.
Between the proportions 0.01 and 0.001 the difference is 0.009, the same difference is between the proportions 0.410 and 0.401, but the ratio of proportions in the first case is 10 (0.01/0.001) and in the second case it is 1.02 (0.410/0.401). In the first case, the success rate (occurrence of a certain event) within a group is 10 times higher than in the other group.
The objective of this paper is to present a routine to analyze qualitative variables in R language from data related to the cleaning of the root canal system with ultrasound and endodontic irrigators.
It started with 50 unirradicular human teeth. The crown was removed and the ducts were cleaned with 1% citric acid in comparison with other irrigation solutions often used in endodontics (5% acetic acid, 5% maleic acid and 17% EDTA) in the presence and absence of ultrasound. The state of the dentinal tubules in the apical, middle and cervical thirds of the root dentine was recorded. Distilled water was used as control.
With the frequencies of occurrence of the different levels of cleaning with citric acid recorded in the samples exposed and not exposed to ultrasound (observed in all thirds), a comprehensive analysis of a categorical response variable in R language was carried out with the following routine:
Generate the contingency table with the frequencies of occurrence of the experimental categories (LU1) by entering the data in the vectors U1 (with the total frequencies of the categories of the experimental factor) and L1 (with the frequencies of the levels of the response variable recorded in each category of the experimental factor).
U1<-c(rep ("CU", 15), rep ("SU", 15))
L1<-c(rep ("TA-0", 1), rep ("TA-1", 7), rep ("TA-2", 5), rep ("TO-3", 2), rep ("TA-0", 0), rep ("TA-1", 5), rep ("TA-2", 6), rep ("TO-3", 4))
LU1<-table (U1, L1)-in LU1 the cross table is stored with the original frequencies
LU1-reports the contingency table stored in object LU1
Prepare the contingency table with the proportions as frequencies relative to the general total (PLU1) and represent it in a separate bar graph (Figures 1 and 2).
PLU1<-prop.table (LU1)-in PLU1 the table of proportions is stored in relation to the total
PLU1-reports the proportions table of the PLU1 object
barplot (PLU1, beside=TRUE, ylab="Proportions according to Total General", legend.text=c ("CU", "SU"))-graph of proportions in separate bars
Create the vector L2 (idem to L1, but joining TA-0 with TA-1 and TA-2 with TO-3, so that all the categories do not have frequencies less than 5) and elaborate the modified contingency table (LU2).
L2<-c (rep("TA-0 and TA-1", 8), rep ("TA-2 and TO-3", 7), rep ("TA-0 and TA-1", 5), rep ("TA-2 and TO-3",10))
LU2<- table (L2, U1)-the LU2 object stores the modified contingency table
Develop the Fisher Exact test on the original contingency table (LU1) and the Chi square test on the modified contingency table (LU2) (the results in (Figure 3).
fisher.test (LU1)-Fisher's exact test on the original LU1 contingency table
chisq.test (LU2)-the Chi square test on the modified contingency table LU2
Determine measures of association based on the test statistic Chi square test (the results are reported in Figure 4).
CCM<-0.543/30-Quadratic Mean Continuity Coefficient: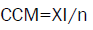
C<-sqrt (0.543/(0.543+30))-Pearson Contingency Coefficient: 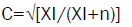
K <-0.133335 * sqrt (2/(2-1))-Fixed Contingency Coefficient: 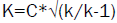
Phi<-sqrt (0.543/30)- Coefficient Phi: 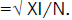
V<-sqrt (0.543/30*(2-1))-Cramer's coefficient 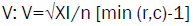
Determine the measures 'difference of proportions' and 'ratio of proportions' between the samples with and without ultrasound at the different levels of the response variable (Figure 5).
d0<-(0.0333-0.0000)-difference between proportions of CU and SU at level TA-0
r0<-(0.0333/0.0000)-relationship between proportions of CU and SU at level TA-0
d1<-(0.2333-0.1666)-difference between proportions of CU and SU at level TA-1
r1<-(0.2333/0.1666)-Relationship between proportions of CU and SU at level TA-1
d2<-(0.1666-0.2000)-difference between proportions of CU and SU at level TA-2
r2<-(0.1666/0.2000)-Relationship between proportions of CU and SU at TA-2
d3<-(0.0666-0.1333)-difference between proportions of CU and SU at the TO-3
r3<-(0.0666/0.1333)-Relationship between proportions of CU and SU at the TO-3
Determine significant differences between proportions of the samples with and without ultrasound (CU and SU) in the different levels of cleaning with citric acid (TA-1, TA-2 and TO-3), generating matrices of 2 columns with pairs to compare and perform the Z tests for proportions (Figure 6).
M1<-matrix (c (7, 5, 23, 25), nrow=2)-matrix to compare CU with SU in TA-1
prop.test (M1)-for the Z test with the M1 matrix
M2<-matrix (c (5, 6, 25, 24), nrow=2)-matrix to compare CU with SU in TA-2
prop.test (M2)-for the Z test with the M2 matrix
M3<-matrix (c (2, 4, 28, 26), nrow=2)-matrix to compare CU with SU in TO-3
prop.test (M3)-for the Z test with the M3 matrix
Table 1 records the frequencies of the different cleaning levels obtained with citric acid 1%, with and without exposure to the ultrasound factor, in comparison with the values obtained with other irrigation solutions.
| Categories | TA-0 | TA-1 | TA-2 | TA-3 | Total |
|---|---|---|---|---|---|
| WU | 1 | 26 | 28 | 20 | 75 |
| AA | 3 | 6 | 6 | 15 | |
| AP | 1 | 4 | 5 | ||
| CE | 2 | 2 | 1 | 5 | |
| ME | 1 | 3 | 1 | 5 | |
| AC | 1 | 7 | 5 | 2 | 15 |
| AP | 1 | 2 | 2 | 5 | |
| CE | 3 | 2 | 5 | ||
| ME | 1 | 3 | 1 | 5 | |
| DW | 1 | 6 | 8 | 15 | |
| AP | 1 | 4 | 5 | ||
| CE | 4 | 1 | 5 | ||
| ME | 1 | 1 | 3 | 5 | |
| MA | 8 | 7 | 15 | ||
| AP | 2 | 3 | 5 | ||
| CE | 3 | 2 | 5 | ||
| ME | 3 | 2 | 5 | ||
| EDTA | 7 | 4 | 4 | 15 | |
| AP | 1 | 1 | 3 | 5 | |
| CE | 3 | 2 | 5 | ||
| ME | 3 | 1 | 1 | 5 | |
| WOU | 2 | 21 | 22 | 30 | 75 |
| AA | 5 | 6 | 4 | 15 | |
| AP | 2 | 3 | 5 | ||
| CE | 3 | 1 | 1 | 5 | |
| ME | 2 | 3 | 5 | ||
| AC | 5 | 6 | 4 | 15 | |
| AP | 2 | 2 | 1 | 5 | |
| CE | 2 | 2 | 1 | 5 | |
| ME | 1 | 2 | 2 | 5 | |
| DW | 15 | 15 | |||
| AP | 5 | 5 | |||
| CE | 5 | 5 | |||
| ME | 5 | 5 | |||
| MA | 3 | 6 | 6 | 15 | |
| AP | 1 | 4 | 5 | ||
| CE | 1 | 2 | 2 | 5 | |
| ME | 2 | 3 | 5 | ||
| EDTA | 2 | 8 | 4 | 1 | 15 |
| AP | 1 | 1 | 2 | 1 | 5 |
| CE | 1 | 3 | 1 | 5 | |
| ME | 4 | 1 | 5 | ||
| Total | 3 | 47 | 50 | 50 | 150 |
WU: With Ultrasound; WOU: Without Ultrasound; AA: Acetic Acid; AC: Citric acid; DW: Distilled Water; MA: Maleic Acid; EDTA: Ethylenediaminetetraacetic Acid; AP: Apical; CE: Cervical; ME: Medium; TA-0: All open tubules; TA-1: >50% open tubules; TA-2: < 50% open tubules; TO-3: All tubules obliterated.
Table 1. Cleaning frequencies of the experimental categories.
Analyzing Figure 2, it is identified that the highest levels of cleanliness correspond to TA-1 in the sample CU (23.33%) and TA-2 in the SU (20%). The TA-0 cleaning level is only recorded in the CU sample, suggesting that citric acid enhances its effect in experimental units exposed to ultrasound. In Figure 1 these results are plotted.
Analyzing the information in Figure 3 (Fisher's exact test on the original contingency table and Chi square test on the modified contingency table), the p-value values (0.713 and 0.4612) greater than the alpha error (0.05) prevent rejecting the hypothesis that raises the independence between the answer variable and the experimental factor, then the "cleaning with citric acid of the root canal system" is not associated to the factor "exposure to ultrasound", considering all thirds.
The differences between the samples with and without ultrasound, in the different levels of cleaning with citric acid, since they are not significant, can be attributed more to the random effect than to the effect of the ultrasound.
Analyzing the measures of association based on the test statistic of the Chi Square test, of Figure 4, the highest value is that of the corrected coefficient of contingency (K=0.1885642), which by its proximity to zero reaffirms the concept of the weak dependence between the response variable and the experimental factor.
Analyzing the information in Figure 5 it is observed that the difference of proportions between CU and SU is of equal magnitude, but in the opposite direction, in levels TA-1 (d1=0.0667) and TO-3 (d3=-0.0667). The ratio of proportions at level TA-1 (r1=1.40) indicates that CU is above the SU by almost 40% and at the TO-3 level (r3=0.499) it is almost 50% lower.
As shown in Figure 6, the Z test determined that the differences are not significant in TA-1 (p=0.7469) or in TO-3 (p=0.667). At the TA-2 level the difference between the proportions between CU and SU is almost nil (d2=-0.0334), the proportion ratio (r2=0.833) indicates that CU is less than the SU by almost 17% and the Z test determines that the difference is not significant (p=1).
The qualitative response variable (cleaning of the root canal system with citric acid), considering the observations in all thirds of the experimental units, showed a weak association with the experimental factor exposure to ultrasound.
No statistical differences were determined between pairs of proportions of the samples exposed and not exposed to the experimental factor, in the different levels of the response variable.
Among the association measures for qualitative variables, the highest value corresponded to the corrected contingency coefficient (K=0.1885642), which due to its proximity to zero induces a weak association between the response variable and the experimental factor; in any case, since the restrictions on the size of the contingency table have been eliminated and the sample size is a result comparable with similar measures.
Citric acid 1% and EDTA 17% are the only irrigators that achieved the maximum level of cleaning of the root canal system, the first in samples with ultrasound and the second in samples without ultrasound. With a simple R language routine, the integral analysis of a qualitative response variable was facilitated. The R language, appreciated for being of free use and having an important field of virtual consultation, through a simple routine facilitated the analysis of a categorical response variable.