ISSN:2321-6212
ISSN:2321-6212
Mohammed Salim Jasim*
Department of Education, Gifted Secondary School, Misan, Iraq
Received: 02-May-2022, Manuscript No. JOMS-22-62515; Editor assigned: 06-May-2022, PreQC No. JOMS-22-6515(PQ); Reviewed: 20-May-2022, QC No. JOMS-22-62515; Revised: 27-May-2022, Manuscript No. JOMS-22-62515(R); Published: 03-Jun-2022, DOI: 10.4172/2321-6212.10.5.005.
Visit for more related articles at Research & Reviews: Journal of Material Sciences
Photonic Crystal Fibers (PCFs) with periodic structure are a never-ending and constantly evolving. In this study was designed fiber photonic crystal is proposed and proven through the Matlab program, which employs the SplitStep Fourier Method (SSFM). Among the consequences demonstrated and studied are the solitons in different order, The impact of changing the radius of air holes on the geography of solitone propagation during fiber has studied, and get supercontinuum generation by increasing the value of radius affecting the third-order soliton. This spectral expansion has important in many modern applications, including medical, industrial and military, as well as have an important role in communication systems.
Photonic Crystal Fibers (PCFs); Split–Step Fourier Method (SSFM); Soliton, Radius air-holes; Supercontinuum generation
A fiber with a silica background and air holes in the cladding region is known as a solid-core photonic crystal fiber. The core is engineered to have a high refractive index compared to the cladding, and laser light are guided through the fiber in same manner that they are guided in traditional fibers, through a modified total internal reflection process [1]. This structure allows a PCF to be built with improved properties than a traditional optical fiber. Endless single-mode operation, manageable dispersion properties, and a high nonlinear coefficient are among these features [2]. Because of these characteristics, the PCF can be used as optical amplifiers, fiber lasers, super continuum generation, and all-optical wavelength transfer, among other applications [3]. The PCF's nonlinearity properties can be improved by achieving a limited effective mode region [4]. The PCF nonlinearity can be made better by a few degrees by decreasing the effective mode region. As the nonlinear coefficient is increased, the fiber becomes a perfect candidate for optical applications, and the detection of nonlinear effects becomes possible at shortest fiber lengths [5-7]. It is therefore possible to achieve a well-guided mode that is limited to a narrow region by varying the sizes of the air-holes within the cladding region. PCFs are used in parametric amplifiers as nonlinear mediums [8]. One can engineer an appropriate mode region that results in the desired nonlinearity by properly tuning the air-hole sizes [9,10]. Fiber Optical Parametric Amplifiers (FOPA) is used in a variety of applications, including in signal processors, converters of optical wavelength and line amplifiers. In this study, a novel PCF with a radius appropriate for air-holes was developed simultaneously with reduced confinement loss, high nonlinearity, low dispersion, and enhanced mode region properties to ensure fabrication. The PCF structure, which has a wide range of applications in optical communications, was created using a modelling methodology specific to this study. The propagation of the first, second and third-order solitone was controlled by controlling the radius of the air-holes.
Photonic Crystal Fibers (PCF)
This form of PCF is made up of a patrol system of air holes rings with a centered solid core that extends over the length of the fiber. They are made of pure silica, and their aim is to lower the cladding's effective refractive index, resulting in a total internal reflection guidance system [11]. Figure 1a illustrates the cross section of the solid core. Figure 1b shows the variation in refractive index with radial size.
Figure 1: Shows (a) Solid core fiber cross-section and (b) refractive index profile [12].
One of the most appealing features of (PCFs) is their ability to remain single-mode over a broad wavelength range, unlike ordinary single-mode fibers, which become multi-mode for wavelengths under their single-mode cut-off wavelength. PCFs with this benefit are known as Endlessly Single-Mode (ESM)–PCFs [13]. The cladding's limited air-filling fraction is needed for a low index-contrast equivalent waveguide, which is required for single-mode operation. At lower wavelengths, the effective index of the cladding would be similar to the refractive index of the silica. This property would reduce the wavelength and maintain the single-mode over a broad wavelength range [14]. The improved optical guiding conditions ensure that PCFs are ideal for the desired application through the following effects:
A-Effective Area A_eff
The light carrying region is commonly referred to as the effective mode area. Electric-field (E) propagation occurs within the core for fundamental propagating mode; as a result, the Effective Mode Area (EMA) of a PCF can be calculated using the equation below [15].
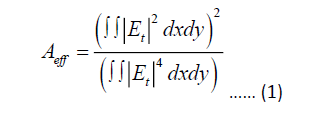
B-Non-linear effect (γ)
The nonlinear effects would be worthwhile with a high optical power density supplied by a limited effective field. The effective region and even the nonlinear coefficient of the PCF background material in relation to the operating wavelength are all directly related to the nonlinear effective or nonlinearity. Equation should be used to look at the nonlinear effect.
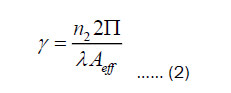
C-Material dispersion
Since the phase index fiber model is made of pure silica glass, the material dispersion (in the core region) can be approximated using the Sellmeier phrase. The wavelength dependency of a material's refractive index is caused by the interaction of the optical mode with ions, gases, or electrons in the material. The dispersion of the materials is determined by Paschotta [16].
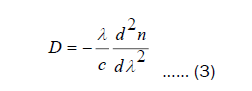
In this study one care about the pulse that takes the form of sech2 pulses, which is known as soliton.
Soliton in photonic crystal fibers
The interesting phenomena of optical solitons, which are solitary optical waves that spread in a particle-like manner over long distances, has been the subject of intensive research in recent decades owing to its critical position in groundbreaking applications such as mode-locking [17], frequency combs [18,19], and supercontinuum generation [20,21], among others [22,23]. One of the specific challenges is the interaction of a laser pulse with a nonlinear photonic crystal. Many papers deal with I building an all-optical switcher based on this relationship, (ii) light translation on photonic crystal defects, and (iii) photonic crystal use in different laser systems [24,25]. The main aim of this study is to investigate in depth the relationship between soliton forming and parameters, as well as to discover a method for regulating soliton parameters and soliton displacement in photonic crystals. The NLSE governs pulse propagation within a PCFs waveguide [26]. Mathematically, it is expressed as Agrawal [27]:
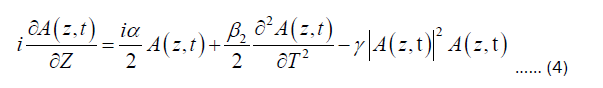
Where A (z,t) denotes the slowly varying pulse envelope amplitude, β2=2nd order dispersion, α=fiber loss, γ=effect of nonlinearity. The effects of fiber loss, dispersion, and nonlinearity on pulses propagating within fibers are described by the three terms on the right side of the equation above. Either dispersive or nonlinear effects prevail along the fiber, depending on the incident pulse parameters-peak strength (P0=1 watt) and initial width (T0=1 ps) of the pulses. Length scaling is given by the Dispersion Length (LD) and Nonlinear Length (LN) values of the fiber over which dispersive or nonlinear effects are important for pulse evolution. Mathematically-based Ambaye and Sakoda[28,29].
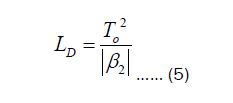
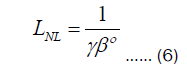
The numerical simulations are carried out using the Split-Step Fourier Method (SSFM). The dispersion is believed to be anomalous (β2=-3) ps2km-1, and there are no losses (α=0) dBkm-1. Nonlinear effects (γ=1), W-1Km-1, where the parameters for the photonic crystal fibers are the distance between holes (ʌ=1.2), wavelength (λ=1.55 nm), number of air-holes (n=8), while diameter air hole (d=0.1,1,1.8) μm, and the results are reached using the MATLAB program.
The simulation results
The effect of diameter air hole on different-order solitons has now been studied and analyzed.
First-order soliton: Sech, pulses of the form are used, i.e. having the following form Wartak [30].
A(0,t)=N Sech(t) …… (7)
Where N corresponds to the order of the pulse. when use N=1, then simply produce the initial pulse
A(0,t)=Sech(t) …… (8)
If the pulse has a "Sech" shape and N=1, it is referred to as the fundamental soliton, and Figure 2 below shows its propagation along the fiber. The diameter of the air holes in the first-order solitone has been controlled as the d=(0.1,01,1.8) μm. As shown in the following results.
Through the results of the change in the diameter of air holes in Figure 2, it is clear that there is a decrease in the amplitude level of the outgoing pulse and that this decrease is gradually decreasing as the diameter of air holes increases. There is also a clear capsizing in the 3D pulse, rather than the widening at the end of the pulse appears as the diameter of the holes increases, the expansion begins from the beginning of the pulse spread. The reason for this is that by increasing the diameter of the holes, the distance travelled by the light propagation through the fiber will lose part of its power, which leads to a decrease in the amplitude of the pulse coming out.
Second–order soliton
In the second order of solitone where N=2, the pulse shows convexities and concavities with distance and time during the change in the value of diameter of air holes as in the 3D soliton, and that the diameter of air holes have the obvious effect in changing the pulse intensity and that the pulse of the output gradually decreases with increased the air holes as shows in 2D soliton, Figure 3 shows that the N=2 soliton spectral components are separated in time as a function of a perturbation introduced at d=0.1,1.
Since the perturbation lowers d=1.8, only partial spectral re-compression appears. Optical pulses in a nonlinear and dispersive medium that show periodic oscillations of their temporal and spectral form are classified as second order. When only the diameter air hole effect is considered, demonstrates the power evolution of pulse shapes. Within two soliton periods, the soliton decay can be seen.
Third order soliton
Third-order soliton, in the case of the third-order soliton with N=3, the pulse exhibits bifurcations, demonstrating the supercontinuum generation by soliton fission with distance and time with air-holes changes d=(0.1,01,1.8) μm, and the output strength a gradually decreases to the point of disappearance almost with increased air-holes as shown in Figure 4.
Higher-order solitons are structurally unstable, according to one study, and a perturbation in the modified Nonlinear Schrödinger Equation (NLSE) can produce significant changes in the nonlinear dynamics of pulse amplitude. In figure 4 it can be observe Positive chirp is produced by SPM, while negative chirp is produced by GVD (D>0). The amount of positive chirp created by SPM is greater than the amount of negative chirp generated by GVD due to the higher intensity; it cannot be cancelled out entirely. As a consequence, the pulse begins to chirp in a constructive manner.
The aim of this study was to look into the decay of various orders of soliton, which were caused by change the diameter of air holes. To complete this mission, a systematic modelling effort for soliton propagation in photonic crystal fibers was undertaken. The split phase Fourier approach was used to create a simulation tool (SSFM). It turns out that when soliton is in the first order, there is an inversion occur in the form of solitone, as well as a decrease in pulse intensity as the diameter of the air holes increases (d=0.1,1,1.8) um.
In the case of second-order solitone, distortions appear when the diameter of air holes are (d=0.1 and 1) um, but the contours of the pulses appear with decrease and regularity of the pulse of the output when d=1.8um.
When the diameter of the air holes a change in the case of the third-order solitone in the super continuum generation phenomenon is clear as well as the chirps is evident as the diameter of the air holes increases and the intensity level of the pulse decreases. The main properties of this study are useful for nonlinear microscopy and spectroscopy applications.