In this paper, we investigate how distributed reinforcement learning-based resource assignment algorithms can be used to improve the performance of a cognitive radio system. Today’s decision making in most wireless systems include cognitive radio systems in development, depends purely on instantaneous measurement. Two system architectures have been investigated in this paper. A point-to-point architecture is examined first in an open spectrum scenario. Then, the distributed reinforcement learning-based algorithms are developed by modifying the traditional reinforcement learning model in order to be applied to a fully distributed cognitive radio system.
Keywords |
| cognitive radio, resource assignment, spectrum sensing, point-to-point architecture, distributed
reinforcement learning |
INTRODUCTION |
| The assignment of spectrum to transmissions and to users is a fundamental issue of wireless communications.
Numerous channel assignment methods have been proposed for sharing the limited physical resource. The traditional
licensed spectrum allocation strategies employed by radio regulatory bodies is very restrictive and extremely inflexible,
resulting in highly underutilized spectrum usage. A fully dynamic spectrum access technique called Cognitive Radio
which was first introduced in [1, 2], has been considered as a potential way to improve the inefficient spectrum
utilization. The inefficient usage of the existing spectrum can be improved through opportunistic access to the licensed
bands without interfering with the existing users. The definition of cognitive radio suggested by ITU-R [3] is: ‘a radio
system employing a technology, which makes it possible to obtain knowledge of its operational environment, policies
and internal state, to dynamically adjust its parameters and protocols according to the knowledge obtained and to learn
from the results obtained’. The fundamental objective of cognitive radio is to enable an efficient utilization of the
wireless spectrum through a highly reliable approach. Although a cognitive radio may be able to analyze the physical
environment before it sets up a communication link, the best system performance is unlikely to be achieved by either a
random spectrum sensing strategy or a fixed spectrum sensing policy. |
| Reinforcement learning (RL), a sub-area of machine learning, uses a mathematical way to evaluate the success level
of actions [4, 5]. Its emphasis on individual learning from the direct interactions with the environment makes it
perfectly suited to distributed cognitive radio scenarios. There are mainly two reasons to consider the reinforcement
learning as the most suitable learning approach for cognitive radio systems. The first reason: Reinforcement learning is
an individual learning approach where the learning agent learns only on local observations and the second is:
Reinforcement learning learns on a trial-and-error basis that no environment model is required. This is also perfectly
suited to cognitive radio systems which constantly interact with an ‘unknown’ radio environment on a trial-and-error
basis. |
| This paper introduces the reinforcement learning-based distributed spectrum sharing (RL-DSS) scheme which
enables efficient usage of spectrum by exploiting users past experience. In the proposed spectrum sharing scheme, a
reward value is assigned to a used resource based on the reward function. Cognitive radio users select spectrum
resources to use based on the weight values assigned to the spectral resources - resources with higher weights are
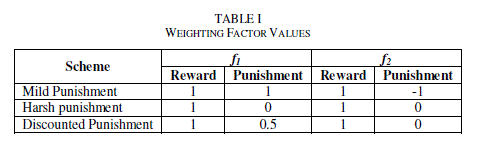
considered higher priority. Furthermore we investigate and compare the system performance of different sets of reward
values which effectively are the weighting factors in the reward function. In fact, we will show how different weighting factor values have significant impact on the system performance, and that inappropriate weighting factor setting may
cause some specific problems. |
| The reminder this paper is organized as follows. The cognitive radio based reinforcement learning model will be
presented in section II. Reinforcement learning-based distributed spectrum sharing algorithm is described in section III.
Section IV presents the key measurements for evaluating the system, Section V presents the simulation results to
validate the analysis, and Section VI concludes the paper. |
SYSTEM MODEL |
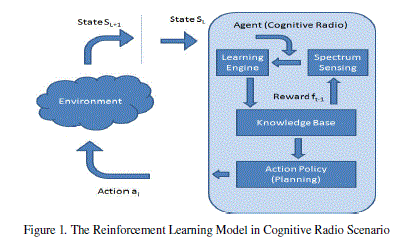
| The reinforcement learning model developed for the cognitive radio scenario is illustrated in Figure 1. The wireless
spectrum is effectively the environment in which cognitive radio (CR) is the learning agent. The way we implement
reinforcement learning in the CR scenario is slightly different from the original reinforcement learning model. This is
caused by a few built-in features of cognitive radio. In the original reinforcement learning system, the value of the
current state s under a policy π which is denoted by Vπ(s) is the basis to choose the action A(s). An optimal policy is
supposed to maximize Vπ(s) at each trial. Vπ(s) is formally defined as [4]: |
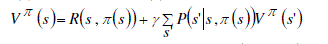 (1) (1) |
 |
 |
 |
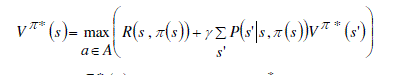 (2) (2) |
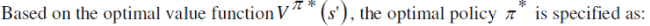 |
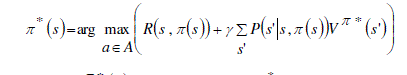 (3) (3) |
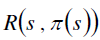 is effectively the cumulative reward in the state of s. The other part of the equation is the expected
feedback of its successor states s’. It can be clearly seen from equation (1) to equation (3) that in order to obtain the optimal policy π*, the information of s’ is vital. Information like the number of potential successor states and the
estimated value of each of the state’s s’ are essential. is effectively the cumulative reward in the state of s. The other part of the equation is the expected
feedback of its successor states s’. It can be clearly seen from equation (1) to equation (3) that in order to obtain the optimal policy π*, the information of s’ is vital. Information like the number of potential successor states and the
estimated value of each of the state’s s’ are essential. |
| Our strategy is to develop a policy π that maps memory (weight values) to action π : W → A instead of the original
approach which maps the state of environment to action π: S → A [12]. On one hand, the agents are fully distributed
in our strategy so that decisions are made only according to the local measurements. It is unlikely for a CR to obtain the
information at the network level. Cognitive radio is able to sense the target spectrum before activation and it is not
supposed to transmit data until unoccupied spectrum has been found. Choosing the most successful spectrum by
reinforcement learning combined with spectrum sensing is the suggested method. A few amendments have been made
to the learning model. The reinforcement learning model which we used consists of [4]: A set of memories, W. W is a
set of weights of the performed actions which are stored in the knowledge base; a set of actions, A; A set of numerical
rewards R. |
| A CR will access the communication resource according to the memory of reinforcement learning. The success level
of a particular action, which is whether the target spectrum is suitable for the considered communication request, is
assessed by the learning engine. Based on the assessment, a reward is assigned in order to reinforce the weight of the
performed action in the knowledge base. Since the actions are all strongly connected to the target resources, the weight
is practically a number which is attached to a used resource and this number reflects the successful level of the
resource. Our goal is to develop an optimal policy mapping weight to action π : W → A that can maximize the value
of the current memory Vπ*(w). Given a set of available weights of used resources and a policy π, the selection of a
specific action is denoted as a = π(w). Then the optimal value function under the optimal policy
π* can be defined as: |
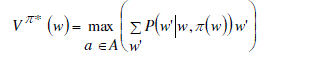 (4) (4) |
Where w is the weight of used resources of an agent at time t, w’ is the expected values of weights after agent takes an action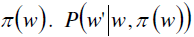 is the probability of selecting an action after taking the action π*. The optimal policy
can be specified as: is the probability of selecting an action after taking the action π*. The optimal policy
can be specified as: |
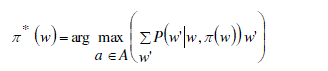 (5) (5) |
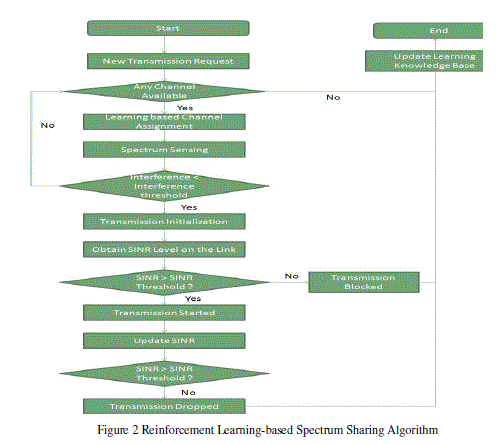
| At each communication request the agent chooses a resource which can maximize V*(w) according to its current
memory. Based on the result, the learning engine updates the knowledge base by a reward r. The inner loop within
cognitive radio in figure 1 will proceed constantly to update the knowledge base; the complexity of the communication
system is reduced. |
| A key element of reinforcement learning is the value function [8]. A CR user updates its knowledge based on the
feedback of the value function. In other words, the CR user adjusts its operation according to the function. The
following linear function is used as the objective function to update the spectrum sharing strategy in this paper [6, 7]: |
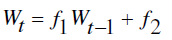 (6) (6) |
 |
 |
DISTRIBUTED REINFORCEMENT LEARNING - CR SPECTRUM SHARING SCHEME |
 |
 |
 |
 |
 |
PERFORMANCE EVALUATION |
| In this paper we evaluated few performance parameters of the system capacity. Signal-to-Interference-plus-Noise-
Ratio (SINR) is used to evaluate link quality, i.e. to determine whether the current user will lose its current service, or
to determine the data rate depending on the adaptive modulation applied to the system. Blocking probability and
dropping probability are normally used to evaluate link based wireless system, e.g. speech-oriented wireless service.
The Cumulative Distribution Function (CDF) is used to process the initial data and to deliver the statistical behavior of
the results. |
| 1) Signal-to-Interference-plus-Noise-Ratio (SINR): Signal-to-Interference-and-Noise Ratio (SINR) [9], also known as
Carrier-to Interference-and-Noise Ratio (CINR), is one of the fundamental parameters to measure the link quality of
users in wireless communication. It is defined by the quotient of the average received signal power (S or C) and the
average received co-channel interference power (I) plus the noise power from other sources (N). In point to point
architecture the SINR has been derived: |
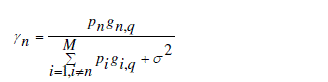 (7) (7) |
| Where p is the transmit power of the n transmitter, g is the gain of the wireless link on channel q, is the noise power. A
frequency separation of backhaul and access is assumed so that the backhaul network and the access network do not
interfere with each other. Then for the backhaul network, SINR measured at ABS n (signal from HBS m in channel q
and sub-channel r) can be derived as: |
 |
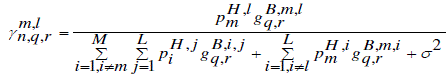 (8) (8) |
 |
Where 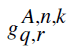 is the link gain between ABS n and MS k. In the denominator first term is the interference from all
the ABSs in other cells that are using the same frequency., and the second one is the interference from other ABSs in
the same cell, and
σ2 is the noise power. is the link gain between ABS n and MS k. In the denominator first term is the interference from all
the ABSs in other cells that are using the same frequency., and the second one is the interference from other ABSs in
the same cell, and
σ2 is the noise power. |
| 2) Cumulative Distribution Function (CDF): As we mentioned before, in order to obtain statistically accurate results
we need to apply Monte Carlo simulation. However, a very large amount of unprocessed data can be expected by
conducting Monte Carlo simulation. Appropriate mathematical analysis in this case is required to show the statistical
behavior of the results. The cumulative distribution function is the main statistical method applied in this report. The
CDF of x is defined as [10]: |
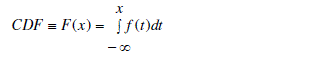 (10) (10) |
| where f(x) is the probability density function of x. The results of our simulation like blocking probability and
dropping probability are mainly measured at regular points in the service area. |
| 3) Blocking Probability and Dropping Probability: Blocking probability and dropping probability [11] are the
measurements we use to evaluate the grade of service. The blocking probability at time t can be defined as: |
 (11) (11) |
| Where P(t) is the blocking probability at time Nb (t) is the total number of blocked activations of the system by
time t and Na (t) is the total number of activations of the system by time t. Similarly, the dropping probability is
defined as follows: |
 (12) (12) |
| Where PD(t) is the dropping probability by time t. ND(t) is the total number of dropped transmissions by time t
and Nsa(t) is the total number of accepted activations by time t. |
SIMULATION RESULTS |
| In this paper we employed an event-based scenario and at each event a random subset of pairs are activated, system
parameters used in this paper is shown in table II. The available spectrum will be partitioned autonomously by
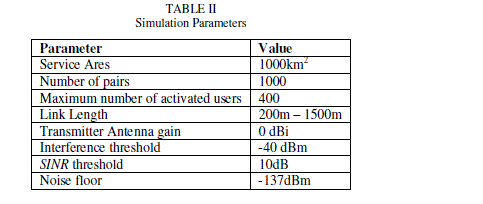
individual reinforcement learning and therefore CR users are able to avoid improper spectrum. Figure 3 (a)-(b)
represent how the channel partitioning emerges during the simulation. A small number of 10 is used in this simulation
to define the number of available channels and the number of users. |
 |
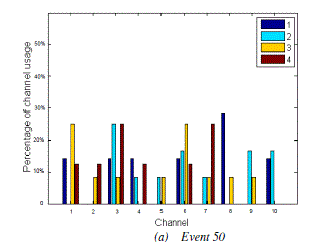 |
| At the beginning of the simulation (Figure 3 (a)), CR users use almost all resources equally. After a certain
simulation time, at event 100 (Figure 3 (b)) a few channels already show their priority to certain users, like user 3
prefers channel 8 and user 2 prefers channel 3. However, the channel usage of user 1 is still fairly equal at this stage. It
can be seen that a spectrum sharing equilibrium is established and therefore the channel usage converged to few
preferred channels. The CR users are able to avoid collisions by utilizing their experience from learning consequently. |
 |
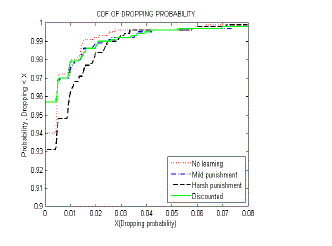 |
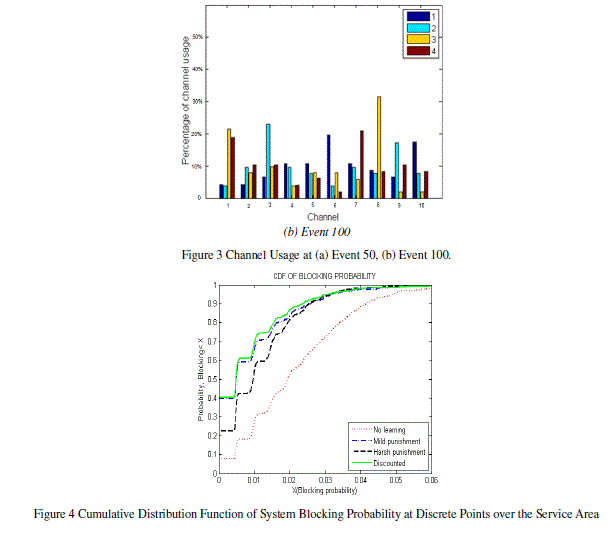
| Figure 4 – Figure 5 illustrate the CDF of Blocking and Dropping probability respectively. Blocking probability is
measured at regular points in the service area and a Cumulative Distribution Function (CDF) of system blocking
probability at these points is derived. In order to analyze the level of system interruption, a CDF of dropping
probability is calculated at the same time. All CR users’ parameters are exactly the same for each scheme evaluation,
with different system performance being caused only by different weighting factor values. |
CONCLUSION |
| In this paper, we introduced a reinforcement learning model for cognitive radio and a few basic reinforcement
learning-based spectrum sharing schemes. By utilizing the ability of learning, cognitive agents can remember their
preferred communication resources and enable an efficient approach to spectrum sensing and sharing accordingly.
Simulation results show that reinforcement learning-based spectrum sharing algorithms achieve a better system
performance compared to non-learning algorithms. |
| |
References |
- J. Mitola and G. Maguire, "Cognitive radio: making software radios more personal," IEEE Personal Communication, vol. 6, pp. 13-18, Aug,1999.
- J. Mitola, "Cognitive Radio: An Integrated Agent Architecture for Software Defined Radio," Ph.D., Teleinformatics, Royal Institute ofTechnology (KTH), May, 2000.
- ITU-R. WRC-12 Agenda Item 1.19: Software-Defined Radio (SDR) and Cognitive Radio Systems (CRS). 2010.
- R. S. Sutton and A. G. Barto, Reinforcement learning : An Introduction: The MIT Press, 1998.
- L. P. Kaelbling, et al., "Reinforcement Learning: A Survey," Journal of artificial intelligence Research, vol. 4, pp. 237-285, May. 1996.
- M. Bublin, et al., "Distributed spectrum sharing by reinforcement and game theory," presented at the 5th Karlsruhe workshop on softwareradio, Karlsruhe, Germany, March. 2008.
- T. Jiang, et al., "Performance of Cognitive Radio Reinforcement Spectrum Sharing Using Different Weighting Factors," presented at theInternational Workshop on Cognitive Networks and Communications (COGCOM) in conjunction with CHINACOM'08, , Hangzhou, China,August, 2008.
- S. Kapetanakis and D. Kudenko, "Reinforcement learning of coordination in cooperative multi-agent systems," presented at the Eighteenthnational conference on Artificial intelligence, Edmonton, Alberta, Canada, 2002.
- S. Saunders, Antennas and propagation for wireless communication systems: Wiley, 1999.
- N. Drakos, "Introduction to Monte Carlo Methods," Computer Based Learning Unit, University of Leeds, Aug 1994.
- J. D. Gibson, The Mobile Communications Handbook, 1st ed.: IEEE Press, 1996.
- T. Jiang, et al., "Two Stage Reinforcement Learning Based Cognitive Radio with Exploration Control," accepted by IET Communications,2009.
|