International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Efficient Techniques for Message Authentication and Communication for Wireless Sensor Network

M.Santhi, D.Suganthi
M.E, Department of CSE, Sri Subramanya College of Engineering and Technology, Palani, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

The Radio Frequency Identification and Wireless Sensor Networks exemplify computationally constrained environments, where the compact nature of the components cannot support complex computations or high communication overhead. On the other hand, such components should support security applications such as message integrity, authentication, and time stamping. The later are efficiently implemented by Hash Message Authentication Codes (HMAC). Current approved implementations of HMAC require resources that cannot be supported in constrained components. The stream ciphering is used in the HMAC mechanism. The same seed based key generation is used in the system. The proposed system is designed to provide authentication, confidentiality and message integrity for wireless sensor node communication. The public key cryptography technique is used to secure the key transfer process. The session-based key is used for message communication. The elliptic curve cryptography technique is used for the key distribution process. The message communication is secured using the RC4 (Rivest Cipher) algorithm. The secure hashing algorithm is used for the message integrity analysis. The Java in Simulation Time (JiST) simulation environment is used for the system development.

Keywords
ECC, Data integrity, Data confidentiality, SHA

INTRODUCTION
Message integrity and authenticity, and replay prevention, are essential in security-related communications. Here, a receiver is expected to be able to verify that a received message, originally transmitted by a valid source, was not changed. Also, the receiver has to verify that the message was not transmitted by a cloned source, and is not a retransmission of an originally genuine message transmitted in the past by a valid source. Technically, verifying message integrity and authenticity is based on the receiver’s ability to prove to itself that the transmitter stores a valid secret key that was used when the message was transmitted. Surely, symmetric and asymmetric cryptographic schemes can also be used in satisfying the above.

AUTHENTICATION
Authentication: authenticating other nodes, cluster heads, and base stations before granting a limited resource, or revealing information here node authentication is implemented by using elliptic curve cryptography algorithm. Which is best method for key secret and suitable for wireless sensor network It has more advantages. To identify the sender node public key is generated by using ECC algorithm by using java Cryptography extensions. Each node generates the key randomly. Before start the transmission pre deployed the key
Elliptic Curve Cryptography (ECC)
? It is a public key cryptography based on elliptic curves over finite fields
? The key values are generated using the curve points
? The system uses 8 bit key values It is used to transfer the session keys

CRYPTOGRAPHY WITH ELLIPTIC CURVES
The principal attraction of ECC compared to RSA is that it offers equal security for a far smaller key size, thereby reducing processing overhead. The addition operation in ECC is the counterpart of modular multiplication in RSA, and multiple addition is the counterpart of modular exponentiation.
The Elliptic Curve Cryptosystem (ECC), whose security rests on the discrete logarithm problem over the points on the elliptic curve. The main attraction of ECC over RSA and DSA is that the best known algorithm for solving the underlying hard mathematical problem in ECC (the elliptic curve discrete logarithm problem (ECDLP) takes full exponential time. RSA and DSA take sub-exponential time. This means that significantly smaller parameters can be used in ECC than in other systems such as RSA and DSA, but with equivalent levels of security. The lack of a subexponential attack on ECC offers potential reductions in processing power and memory size. These advantages are specially important in applications on constrained devices.
In practical terms, the performance of ECC depends mainly on the efficiency of finite field computations and fast algorithms for elliptic scalar multiplications. In addition to the numerous known algorithms for these computations, the performance of ECC can be increased by selecting particular underlying finite fields and/or elliptic curves. For ECC, we are concerned with a restricted form of elliptic curve that is defined over a finite field. Of particular interest for cryptography is what is referred to as the elliptic group mod p, where p is a prime number. This is defined as follows. Choose two nonnegative integers, a and b, less than p that satisfy:
4a3 + 27 b2 (mod p) ≠ 0, (3)
Then Ep(a, b) denotes the elliptic group mod p whose elements (x, y) are pairs of nonnegative integers less than p satisfying:
y2 ≡ x3 + ax + b (mod p) (4)
together with the point at infinity O. The elliptic curve discrete logarithm problem can be stated as follows. Fix a prime p and an elliptic curve.
Q= xP (5)
where xP represents the point P on elliptic curve added to itself x times. Then the elliptic curve discrete logarithm problem is to determine x given P and Q. It is relatively easy to calculate Q given x and P, but it is very hard to determine x given Q and P.

ECC ENCRYPTION/DECRYPTION
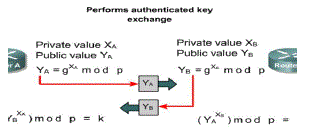
Several approaches to encryption/decryption using elliptic curves have been analyzed. This paper describes one of them. The first task in this system is to encode the plaintext message m to be sent as an x-y point Pm. It is the point Pm that will be encrypted as a cipher text and subsequently decrypted. Note that we cannot simply encode the message as the x or y coordinate of a point, because not all such coordinates are in Ep(a, b). There are approaches to encoding. We developed a scheme that will be reported elsewhere. As with the key exchange system, an encryption/decryption system requires a point G and an elliptic group Ep(a, b) as parameters. Each user A selects a private key nA and generates a publickey
PA = nA x G. (6)
To encrypt and send a message Pm to B, A chooses a random positive integer x and produces the cipher text Cm consisting to the pair of points[7]
Cm = {xG, Pm + xPB} (7)
Note that A has used B’s public key PB.
To decrypt the cipher text, B multiplies the first point in the pair by B’s secret key and subtracts the result from the second point:
Pm + xPB – nB(xG) = Pm + x(nBG) – nB(xG) = Pm
A has masked the message Pm by adding xP B to it. Nobody but A knows the value of x, so even though PB is a public key, nobody can remove the mask xPB. However, A also includes a “clue,” which is enough to remove the mask if one knows the private key nB. For an attacker to recover the message, the attacker would have to compute xgiven G and xG, which is hard .

DATA CONFIDENTIALITY
Data confidentiality is the most important issue in network security. Every network with any security focus will typically address this problem first. In sensor networks, the confidentiality relates to the following
? A sensor network should not leak sensor readings to its neighbors. Especially in a military application, the data stored in the sensor node may be highly sensitive.
? In many applications nodes communicate highly sensitive data, e.g. ,key distribution, therefore it is extremely important to build a secure channel in a wireless sensor network.
? Public sensor information, such as sensor identities and public keys, should also be encrypted to some extent to protect against traffic analysis attacks.
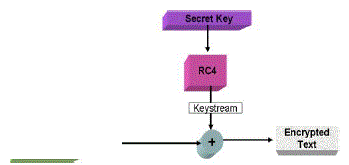
The standard approach for keeping sensitive data secret is to encrypt the data with a secret key that only intended receivers possess, thus achieving confidentiality. In cryptography, RC4 (also known as A RC4 or A RCFOUR meaning Alleged RC4, is the most widely-used software stream cipher (to secure wireless networks). While remarkable for its simplicity and speed in software,Description.
RC4 generates a pseudorandom stream of bits (a keystream) which, for encryption, is combined with the plaintext using bit-wise exclusive-or; decryption is performed the same way (since exclusive-or is a symmetric operation). To generate the keystream, the cipher makes use of a secret internal state which consists of two parts: A permutation of all 256 possible bytes (denoted "S" below).
The permutation is initialized with a variable length key, typically between 40 and 256 bits, using the key-scheduling algorithm (KSA). Once this has been completed, the stream of bits is generated using the pseudo-random generation algorithm.
The key-scheduling algorithm (KSA)
The key scheduling algorithm is used to initialize the permutation in the array "S". "key length" is defined as the number of bytes in the key and can be in the range 1 ≤ key length ≤ 256, typically between 5 and 16, corresponding to a key length of 40 – 128 bits. First, the array "S" is initialized to the identity commutation. S is then processed for 256 iterations in a similar way to the main PRGA algorithm, but also mixes in bytes of the key at the same time.
for i from 0 to 255
S[i] := i
endfor
j := 0
for i from 0 to 255
j := (j + S[i] + key[i mod keylength]) mod 256
swap(&S[i],&S[j])
endfor
The pseudo-random generation algorithm (PRGA)
The lookup stage of RC4. The output byte is selected by looking up the values of S(i) and S(j), adding them together modulo 256, and then looking up the sum in S; S(S(i) + S(j)) is used as a byte of the key stream, K. For as many iterations as are needed, the PRGA modifies the state and outputs a byte of the keystream. In each iteration, the PRGA increments i, adds the value of S pointed to by i to j, exchanges the values of S[i] and S[j], and then outputs the value of S at the location S[i] + S[j] (modulo 256). Each value of S is swapped at least once every 256 iterations.
i := 0
j := 0
while GeneratingOutput:
i := (i + 1) mod 256
j := (j + S[i]) mod 256
swap(&S[i],&S[j])
output S[(S[i] + S[j]) mod 256]
endwhile
Many stream ciphers are based on linear feedback registers(LFSRs), which while efficient in hardware are less so in software. The design of RC4 avoids the use of LFSRs, and is ideal for software implementation, as it requires only byte manipulations. It uses 256 bytes of memory for the state array, S[0] through S[255], k bytes of memory for the key, key[0] through key[k-1], and integer variables, i, j, and k. Performing a modulus 256 can be done with a bitwise AND with 255 (or on most platforms, simple addition of bytes ignoring overflow).

DATA INTEGRITY
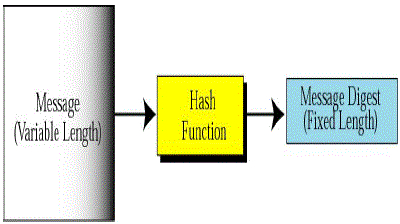
With the implementation of confidentiality, an adversary may be unable to steal information. However, this doesn’t mean the data is safe. The adversary can change the data, so as to send the sensor network into disarray. For example, a malicious node may add some fragments or manipulate the data within a packet. This new packet can then be sent to the original receiver. Data loss or damage can even occur without the presence of a malicious node due to the harsh communication environment. Thus, data integrity ensures that any received data has not been altered in transit. SHA hash functions
Secure Hash Algorithm (SHA)
? The secure hashing algorithm is used for message integrity
? The SHA algorithm generate signature or message digest with 160 bits
? The signature generation is done at sender and receiver nodes.
? The signature verification is used for integrity check.
The SHA hash functions are a set of cryptographic functions designed by the National security agent(NSA). SHA stands for Secure Hash Algorithm. The three SHA algorithms are structured differently and are distinguished as SHA- 0, SHA-1, and SHA-2. The SHA-2 family uses an identical algorithm with a variable digest size which is distinguished as SHA-224, SHA-256, SHA-384, and SHA-512.SHA-1 is the best established of the existing SHA hash functions, and is employed in several widely used security applications and protocols. Simulators in simulate WSNs.
SHA1 Message Digest Algorithm
This section describes the SHA1 algorithm - a 6-step process of padding of '1000...', appending message length, preparing 80 process functions, preparing 80 constants, preparing 5 word buffers, processing input in 512 blocks.
SHA1 algorithm consists of 6 tasks:
Task 1. Appending Padding Bits. The original message is "padded" (extended) so that its length (in bits) is congruent to 448, modulo 512. The padding rules are:
• The original message is always padded with one bit "1" first.
• Then zero or more bits "0" are padded to bring the length of the message up to 64 bits fewer than a multiple of 512.
Task 2. Appending Length. 64 bits are appended to the end of the padded message to indicate the length of the original message in bytes. The rules of appending length are:
• The length of the original message in bytes is converted to its binary format of 64 bits. If overflow happens, only the low-order 64 bits are used.
• Break the 64-bit length into 2 words (32 bits each).
• The low-order word is appended first and followed by the high-order word.
Task 3. Preparing Processing Functions. SHA1 requires 80 processing functions defined as:
f(t;B,C,D) = (B AND C) OR ((NOT B) AND D) ( 0 <= t <= 19)
f(t;B,C,D) = B XOR C XOR D (20 <= t <= 39)
f(t;B,C,D) = (B AND C) OR (B AND D) OR (C AND D) (40 <= t <= 59)
f(t;B,C,D) = B XOR C XOR D (60 <= t <= 79)
Task 4. Preparing Processing Constants. SHA1 requires 80 processing constant words defined as:
K(t) = 0x5A827999 ( 0 <= t <= 19)
K(t) = 0x6ED9EBA1 (20 <= t <= 39)
K(t) = 0x8F1BBCDC (40 <= t <= 59)
K(t) = 0xCA62C1D6 (60 <= t <= 79)
Task 5. Initializing Buffers. SHA1 algorithm requires 5 word buffers with the following initial values:
H0 = 0x67452301
H1 = 0xEFCDAB89
H2 = 0x98BADCFE
H3 = 0x10325476
H4 = 0xC3D2E1F0
Task 6. Processing Message in 512-bit Blocks. This is the main task of SHA1 algorithm, which loops through the padded and appended message in blocks of 512 bits each. For each input block, a number of operations are performed. This task can be described in the following pseudo code slightly modified from the RFC 3174's method 1:
Input and predefined functions:
M[1, 2, ..., N]: Blocks of the padded and appended message
f(0;B,C,D), f(1,B,C,D), ..., f(79,B,C,D): Defined as above
K(0), K(1), ..., K(79): Defined as above
H0, H1, H2, H3, H4, H5: Word buffers with initial values
Algorithm:
For loop on k = 1 to N
(W(0),W(1),...,W(15)) = M[k] /* Divide M[k] into 16 words */
For t = 16 to 79 do:
W(t) = (W(t-3) XOR W(t-8) XOR W(t-14) XOR W(t-16)) <<< 1
A = H0, B = H1, C = H2, D = H3, E = H4
For t = 0 to 79 do:
TEMP = A<<<5 + f(t;B,C,D) + E + W(t) + K(t)
E = D, D = C, C = B<<<30, B = A, A = TEMP
End of for loop
H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E
End of for loop
Output: H0, H1, H2, H3, H4, H5: Word buffers with final message digest
The contents in H0, H1, H2, H3, H4, H5 are returned in sequence the message digest.

CONCLUSION
RFID and Wireless Sensor Networks pose a need for efficient implementation of MAC. To achieve efficiency, while not sacrificing security, there is a need to evaluate new approaches, while also utilizing any characteristic of the specific implementation ofecc,ECC,RC4and SHA 1 that can enhance efficiency. The key transmission is secured by using ECC. A complete highly compact RC4 implementation, based on stream ciphering, was presented. The principle was to implement a hash transformation based on the stream cipher, where the strength of the hash is associated with the underlying security of the cipher. The hash is then utilized to implement SHA1,for message integrity. These algorithms are supported to minimum configuration environment.
To improve the message authentication and communication on wireless Sensor network, by reducing the encryption time, speed will increased. During the transmission, if any node will fail to activate, a Node Reflector is used to avoid this delay .Otherwise remove the node if it is not in the cluster. It saves the energy and improve the message secret. Then also improve the key distribution for secured data transmission.
 

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
 

References