Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Electrostatic Micro-actuator Structural Analysis Using Genetic Algorithm

Atal Anil Kumar
Student, Dept. of Robotics Engineering, University of Genoa, Genoa, Italy
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This study is devoted to providing predictions of the pull-in parameters (pull-in voltage and pull-in displacement) of electro-statically actuated micro-beams based on a continuous model using Genetic Algorithm (GA) technique. A phenomenon in which the actuated electrode comes in direct contact with the fixed electrode due to the electrostatic force is called pull-in instability. Accurate determination of pull-in parameters is vital in the design of electrostatic micro-actuators. The non-linear electrostatic beam equation is solved using GA and a comparative study is presented with the solutions obtained using COMSOL and Energy technique.

Keywords
Pull in parameters, electro-statically actuated Micro-beams, Genetic Algorithm.

INTRODUCTION
Recent advances in the technology of MEMS have accelerated the design and application of micro-sensors and actuators based on electrostatic actuation, such as pressure sensors [1, 2], microphones [3, 4] and optical/ RF switches [5–9] invaried structures. Electrostatic devices are in fact capacitors that are composed of one deformable electrode and another fixed electrode (backplate).With the application of across voltage the flexible electrode deforms and then touches the fixed electrodes for different application objectives. Some applications, such as microphones [3, 4] or pressure sensors [1, 2], must be only operated within a safe range without pull-in occurrence, while others, such as optical/RF switches [5–9], need to tune the bias voltage across the pull-in back and forth to alternate switch on and off. It is therefore very essential to understand and know in advance the behaviour of such devices on the application of an applied potential.
The problem of electrostatic-structural analysis is a coupled problem in which the displacement is dependent on the force and the force is dependent on the displacement. The governing differential equation of such an electrostatic elastic system is a nonlinear one and has to be solved numerically in majority of the cases. A variety of numerical techniques are used to extract the various quantities of interest. An algorithm based on displacement of actuator electrode was developed to find out the pull-in parameters [10]. In addition to this, use of differential quadrature method [11], Lagrangian approach [12] and Lagrange multipliers technique [13] can also be found in the past. Recently Finite Difference Method (FDM) was used to accurately determine the pull-in parameters [14]. While performing the finite element simulation, the problem has to be solved in multiphysics environment, in which the structural and electrostatic solvers are separately executed.
During the last 25 years there has been significant development in methods for solving the complex problems faced by the scientific community. Genetic Algorithm has shown to be a valuable and robust technique in assisting engineers to solve complex problems in a number of diverse engineering applications such as system identification[15,16], controller design[17,18], neural networks [19,20], fuzzy systems[21,22], image processing [23,24], signal processing[25,26], etc. This is undoubtedly due to its ability to solve multi-objective, non-differentiable problems with greater reliability. Salhi gives a general overview [27] of heuristic search methods including GA’s.
In the proposed work we compare the results obtained from Genetic Algorithm with the solutions given by the earlier researchers to prove that the proposed method is reliable and can be used for further probe of the problem. In the section that follows an explanation of the problem considered, the proposed algorithm, the values obtained, the results and finally the conclusion has been presented.

PROBLEM DESCRIPTION
In order to gain an insight into the electrostatic elastic interactions that take place in the actuator, we consider a parallel plate model.
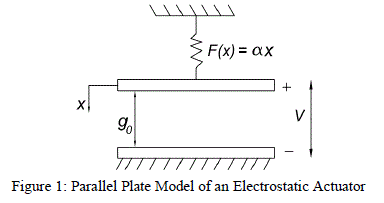image
Figure 1 shows the simplified lumped spring-mass model of a parallel plate electrostatic actuator. It consists of a pair of rigid plates maintained at different electric potentials and separated by a nominal gap g0. This configuration forms a capacitor having capacitance C given by,
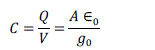image (1)
Where, Q is the charge, V is the voltage, ∈0 is the permittivity of free space, A is the area of overlap and g0 is the distance between two plates. A small increase in the potential difference results in the charge redistribution on the surface of the plates, leading to generation of attractive electrostatic force between the two plates. This force pulls the top plate in the downward direction. Thus by controlling the potential difference between the two capacitor plates, one can have control over the displacement of the movable plate.
Although the nature of pull-in instability appears to be simple in-case of parallel plate model, the mechanics of pull-in instability is quite complicated in a practical actuator system. Parallel plate model is only an idealization of the practical system, which is used to have a simplified insight. The practical concern involves the analysis of continuous mechanical systems like micro-beams, membranes or plates, which themselves can offer many structural analysis challenges. The problem under consideration is a coupled field problem where the primary objective is to determine the parameters like pull-in displacement and pull-in voltage.
Hence the problem requires mainly the solution of nonlinear differential equation in case of a model of continuous mechanical systems such as a micro-beam. The governing differential equation of the beam deflection is given by making use of the Euler-Bernoulli beam theory as stated below,
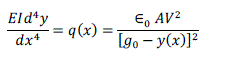image (2)
Where, y is the deflection of the beam, which is a function of the coordinate x measured along its length. A is the cross sectional area, V is the applied potential difference between the two electrodes, ∈0 is the permittivity of the free space and g0 is the initial separation between the two electrodes. As such, continuous mechanical system’s model is more appropriate for the analysis of a practical actuator system.
It is well understood that the analytical solution to the nonlinear differential equation is difficult to obtain and it is generally solved numerically. Finite Difference Method (FDM), Finite Element Method (FEM) are some of the numerical methods that are utilized to arrive at the solution. A newer scheme based on Genetic Algorithm is proposed for the static analysis of the coupled electrostatic-elastic problem.

GENETIC ALGORITHM
Genetic algorithm is an adaptive heuristic search algorithm premised on the evolutionary ideas of natural selection. Genetic Algorithm was introduced by Holland [28] as a computational analogy of adaptive system. The basic concept of genetic algorithm is designed to simulate processes in natural system necessary for evolution, specifically those following the principle of survival of fittest. As such they represent an intelligent exploitation of a random search within a defined search space to solve a problem. The appeal of GA comes from its simplicity and elegance as a robust search algorithm as well as from their power to discover good solution rapidly for difficult high dimensional problem. GA was modelled loosely employing a population of individuals that undergo selection in the presence of variation inducing operators like cross-over, mutation. A fitness function is used to evaluate individuals and reproductive success varies with fitness. There are two important issues in the evolution process of genetic search: population diversity and selective pressure [29]. Sampling mechanisms are attempts to strike a balance between these two factors.
A genetic algorithm is typically initialized with a random population consisting of between 20-100 individuals. This population (mating pool) is usually represented by a real-valued number or a binary string called a chromosome. How well an individual performs a task is measured and assessed by the objective function. The objective function assigns each individual a corresponding number called its fitness. The fitness of each chromosome is assessed and a survival of the fittest strategy is applied. In this work, residue minimization technique is used to assess the fitness of each chromosome. There are three main operators for a genetic algorithm; these are known as reproduction, crossover and mutation.

A. Reproduction
Reproduction is a method that stochastically selects the individuals from the population according to their fitness, the higher the fitness, the more chance an individual has to be selected for the next generation. Natural selection tends to eliminate animals with poor foraging strategies through methods of locating, handling and ingesting food and favours the propagation of those genes that have successful foraging strategies. There are three types of selection: fitness proportionate selection, ranking method and tournament selection.

B. Cross over
In crossover, new strings are created by exchanging information among strings of the mating pool based on a probability ranging from 0.5 to 0.8. Actually strings are picked from the mating pool and some portions of the strings are exchanged between the strings. A string point crossover operator is used in this work which is performed randomly by choosing a crossing site along the string and by exchanging all bits on the right side of the crossing site.

C. Mutation
Mutation is the occasional random alteration of a value of a string position. It is considered a background operator in the genetic algorithm. The probability of mutation is normally low because a high mutation rate would destroy fit strings and degenerate the genetic algorithm into a random search. Once a string is selected for mutation, a randomly chosen element of the string is changed or ‘mutated’.

D. Implementation of GA
The optimal values of the pull-in parameters are found using GA. All possible sets of the parameter values are chromosomes whose values are adjusted so as to minimize the objective function. As explained earlier the equation to be solved using GA is
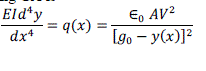image (3)
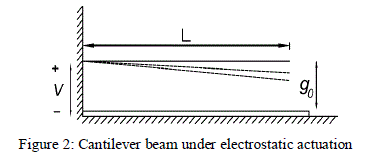image
Consider the cantilever beam under quasi-static condition as shown in figure 2. The figure shows a simple cantilever of length L, width b and thickness t, used as a movable electrode in the electrostatic actuator system. The fixed electrode is located at the bottom and the two electrodes are separated by an initial gap g0. When voltage V is applied across the two electrodes, the cantilever deforms under the action of electrostatic force. The deflected shapes of the cantilever are shown by the dotted curves.
Initially we assume that, the deflected shape of the cantilever is defined by a fourth order polynomial given by
image (4)
Where, x is measured from the fixed end along the length of the cantilever. This assumption of the polynomial equation is justified as the differential equation of the cantilever beam is of fourth order. Using the appropriate boundary conditions for the cantilever, the assumed displaced shape can be written in terms of a4 as
image (5)

E. Objective Function
The objective function used in the present work is residue minimization technique which is explained below. Considering the fourth order polynomial mentioned above and the governing differential equation, we get
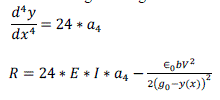image(6) & (7)
The objective function is as given below,
objective function = image (8)

RESULTS AND DISCUSSION
Consider the following dimensions and parameters of a typical prismatic microcantilever beam[30].
L= 100μm, b= 50μm, h= 3μm, g= 1μm,E=169*10^9 N/m2, ∈0= 8.854 * 10-12F/m
GA was implemented for these parameters using MATLAB/Simulink software.
The initialized parameters for the problem considered are as follows:
Population Type: Double Vector
Population size: 20
Creation Function: uniform
Fitness Scaling: Rank
Selection Function: Roulette
Crossover Fraction: 0.8
Mutation: Gaussian with scale=1, shrink=1
Crossover: Scattered
Migration: Both directions
Termination of optimization algorithm can take place either when the maximum number of iterations gets over or with the attainment of satisfactory fitness value. In this work the termination criteria is considered to be the attainment of satisfactory fitness value beyond which the change in the value of fitness function is minimum. For each iteration the best among the 1000 particles considered as potential solution are chosen. Therefore the best value for 1000 iterations is sketched with respect to iteration.
Based on GA we get the voltage displacement characteristics curve as shown below. The curve obtained by using GA is compared with the COMSOL and Energy technique.
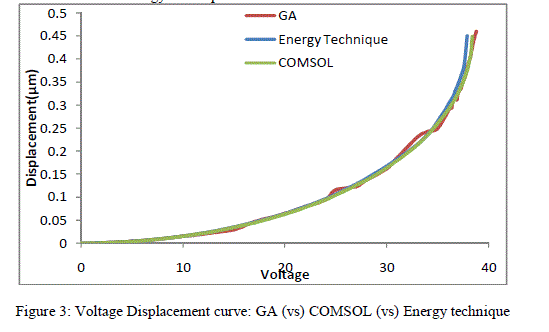image
Figures 3 shows that the proposed GA technique gives a plot which matches well with the other techniques that were used to solve the equation. For this case the results published in the literature and the results obtained by the proposed technique are tabulated as shown below. The values prove that this technique can very well be applied to the problem considered.
image
It is clear from table 1 that the percentage difference in the values of pull-in displacement using Energy technique and GA is 0.75 % which means that the technique used is very reliable and can give an accurate output. Also the percentage difference in the values of pull-in voltage is 0.2%, 0.35%, 0.37% and 0.12% respectively. Apart from this, a table has been given to analyse the behaviour of the beam before the occurrence of pull-in.
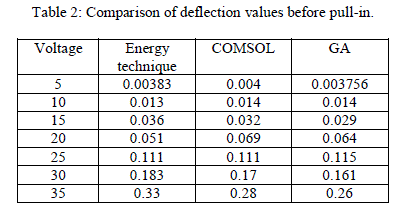image
Table 2 further strengthens our belief that the implementation of GA can be useful to analyse the behaviour of the beam as the values obtained are similar to that of the values obtained in other techniques..This is a clear indication of the ability of the algorithm to give an output which satisfies the necessary objective function.

CONCLUSION
Since the algorithm gives satisfactory output for a cantilever beam, it can be further applied to a fixed-fixed beam and the values can be compared with the existing solutions. Also this algorithm can be used to find out means of extending the travel range of electrostatic micro-actuators and can be used to optimise the values that were used earlier.

References
  1. Ho JJ, Fang YK, Hsieh MC, Ting SF, Chen GS, Ju MS, Chen TY, Huang CR and Chen CY, “Development of A micro-electro mechanical system pressure sensor for rehabilitation engineering applications”, Int.J.Electro,.87. 757–67,2000.
  2. Sallese JM, Grabinski W, Meyer V, Bassin C and Fazan P, “Electrical modeling of a pressure sensor MOSFET”, Sensors and Actuators, 94, 53– 58,2001.
  3. Pedersen M, OlthuisWand Bergveld P, “A silicon Condenser microphone with polymide diaphragm and backplate”, Sensors and Actuators, 63/2, 97–104,1997.
  4. Pedersen M,Olthuis W and Bergveld P, “High-performance condenser microphone with fully integrated CMOS amplifier and DC –DC voltage converter”, J.Microelectromech.Systems, 7, 387–94,1998.
  5. Chik KD, “Precision wavelength light sources for dense WDM system”, Proc. SPIE Int. Soc. Opt. Eng., 12, 972–8,1997.
  6. Liu AQ, Zhang XM and Tang DY, “MEMS widely tunable lasers for WDM system applications”, Proc .SPIE Int. Soc. Opt. Eng., 4907, 186– 94,2002.
  7. Zhang XM, Liu AQ and Ang., “MEMS variable optical attenuator using low driving voltage for DWDM systems”, Electron. Letters, 38, 382– 3,2002.
  8. Jiang L, Shi Y, Ding Y, Lai Z and Zhu, “Numerical analysis of pull-in voltage for contact MEMS switches in switched-line phase shifter application ,“ Proc. SPIE Int. Soc. Opt. Eng, 5774, 587–90,2005.
  9. Zhu Y and Espinosa HD, “Effect of temperature on capacitive RF MEMS switch performance—a coupled-field analysis”, J. Micromech. Microeng,14, 1270–9,2004.
  10. O.Degani, D.Elata, and Y.Nemirovsky, “An efficient dipie algorithm for cad of electro-statically actuated mems devices,” Journal of Microelectromechanical Systems 11(5),pp.612–620,2002.
  11. J.Kuang and C.Chen, “The non linear electrostatic behaviour for shaped electrode actuators”, International Journal of Mechanical Sciences 47,pp.1172–1190,2005.
  12. G.Li and N.Aluru, “A Lagrangian approach for electrostatic analysis of deformable conductors”, Journal of Micro-electromechanical Systems, 11(3),pp.245–254,2002.
  13. M.Abdalla, C.Reddy, W.Faris, and Z.Gurdal, “Optimal design of an electro-statically actuated micro-beam for maximum pull-in voltage,” Computers and Structures 83, pp.1320–1329,2005.
  14. H.Sadeghian and G.Rezazadeh, “The influence of stress gradient on the pull-in phenomena of micro-electromechanical switches”, Journal of Physics 34,pp.1117–1122,2006.
  15. Kristinsson K, Dumont GA, “System-identification and control using genetic algorithms”, IEEE Transactions on Systems Man, and Cybernautics, 22(5):1033-1046, 1992.
  16. Luh GC, Wu CY, “Non-linear system identification using genetic algorithms”, Proceedings of the Institution of Mechanical Engineers Part IJournal of Systems and Control Engineering, 213(12):105-118,1999.
  17. Warwick K, Kang YH, “Self-tuning proportional integral and derivative controller based on genetic algorithm least squares”, Proceedings of the Institution of Mechanical Engineers Part I-Journal of Systems and Control Engineering, 212(16):437-448,1998.
  18. Michalewicz Z, Janikow CZ, Krawczyk JB, “A modified genetic algorithm for optimal control problems”, Computers and Mathematics with Applications, 23(12):83-94,1992.
  19. Nissinen AS, Koivo HN, Koivisto H, “Optimization of neural network topologies using genetic algorithm”, Intelligent Automation and Soft Computing, 5(3):211-223,1999.
  20. Bornholdt S, Graudenz D, “General asymmetric neural networks and structure design by genetic algorithms”, Neural Networks,5(2):327- 334,1992.
  21. Shimojima K, Fukuda T, Hasegawa Y, “Self-tuning fuzzy modelling with adaptive membership function, rules, and hierarchical structure based on genetic algorithm”, Fuzzy Sets and Systems, 71(3):295-309,1995.
  22. Wong SV, Hamouda AMS, “Optimization of fuzzy rules design using genetic algorithm”, Advances in Engineering Software,31(4):251- 262,2000.
  23. Andrey P, Tarroux P, “Unsupervised image segmentation using a distributed genetic algorithm”, Pattern Recognition, 27(5):659-673,1994.
  24. Delibasis KK, Undrill PE,Cameron GG, “Genetic algorithm implementation of stack filter design for image restoration”, IEEE Proceedings- Vision Image and Signal Processing, 143(3):177-183,1996.
  25. Shao XG, Yu F, Kou HB, Cai WS, Pan ZX, “A wavelet-based genetic algorithm for compression and de-noising of chromatograms”, Analytical Letters, 32(9):1899-1915,1999.
  26. Hung JC, Chen BS, “Genetic algorithm approach to fixed-order mixed H-2/H- infinity optimal deconvolution filter designs”, IEEE Transactions on Signal Processing, 48(12):3451-3461,2000.
  27. S.Salhi, “Heuristic search methods In G.A”, Marcoulides(Ed.),Modern methods for business research Lawrence Erlbaum Associates, chapter6,p.147,1998.
  28. Holland JH, “Adaptation in natural and artificial systems”, University of Michigan Press, AnnArbor. 1975.
  29. Michalewicz Z, “Genetic algorithms data structures evolution programs”,3rdedn.Springer,NewYork,1996.
  30. Chowdhury S, Ahmadi M, Miller W, “ A closed form model for Pull-in voltage of Electro-statically actuated cantilever beam”, Journal of Micromechanics Microengineering,15, pp-756-763,2005.