Keywords
|
| BLP computation, ECDLP, DT, Secure Outsourcing Confidential data. |
INTRODUCTION
|
| Cloud computing is a term that involve to deliver the services over the Internet. Cloud computing allows computer users to conveniently rent access to fully featured applications, to software development and deployment environments, and to computing infrastructure assets such as network-accessible data storage and processing. Cloud computing is a model for enabling convenient, on-demand network access to a shared pool of configurable computing resources (e.g., networks, servers, storage, applications, and services) that can be rapidly provisioned and released with minimal management effort or service provider interaction It enables customers with limited computational resources to outsource their large computation workloads to the cloud, and economically enjoy the massive computational power, bandwidth, storage, and even appropriate software that can be shared in a pay-per-use manner. Security is the primary obstacle that prevents the wide adoption of this promising computing model, especially for customers when their confidential data are consumed and produced during the computation. Depending on an organization's requirements, different technologies and configurations are appropriate. To understand which part of the spectrum of cloud systems is most appropriate for a given need, an organization should consider how clouds can be deployed (deployment models), what kinds of services can be provided to customers (service models), the economic opportunities and risks of using cloud services (economic considerations), the technical characteristics of cloud services such as performance and reliability (operational characteristics), typical terms of service (service level agreements), and the security opportunities and risks (security). To combat against unauthorized information leakage, sensitive data have to be encrypted before outsourcing. End to- end data confidentiality assurance should be provided when outsourcing the data through cloud services. Cloud storage services may be accessed through a web service application programming interface (API), or through a Web-based user interface. |
| These services are classified as : Infrastructure-as-a-Service (IaaS), Platform-as-a-Service (PaaS) and Software-as-a- Service (SaaS). A cloud service has three major differences when compared to traditional services. It is sold on demand, user has to pay only for what they use; it is elastic - a user can have as much or as little of a service as they want at any given time and the service is fully managed and controlled by the cloud service provider. |
BACKGROUND:
|
| Over the past 30 years, public key cryptography has become a chief support for secure communications over the Internet and throughout many other forms of communications. It provides the foundation for both key management and digital signatures. In key management, public key cryptography is used to distribute the secret keys used in other cryptographic algorithms (e.g. DES). For the past 20 years, Internet communications have been secured by the first generation of public key cryptographic algorithms developed in the mid-1970's. They form the basis for key management and authentication for IP encryption web traffic and secure electronic mail. |
| The two noteworthy first generation public key algorithms used to secure the Internet today are known as RSA and Diffie-Hellman (DH). The security of the first is based on the difficulty of factoring the product of two large primes. The second is related to a problem known as the discrete logarithm problem for finite groups. Both are based on the use of elementary number theory. Interestingly, the security of the two schemes, though formulated differently, is closely related. Elliptic curve cryptography has also been an active area of study in academics. Similar to both RSA and Diffie- Hellman, the first years of analysis yielded some vulnerable cases for elliptic curve parameters that one should avoid. However, unlike the RSA and Diffie-Hellman cryptosystems that slowly yielded to increasingly strong attack algorithms, elliptic curve cryptography has remained at its full strength since it was first presented in 1985. |
| The algorithm was approved by NIST in 2006. In 2013, the New York Times revealed that Dual Elliptic Curve Deterministic Random Bit Generation (or Dual_EC_DRBG) had been included as a NIST national standard due to the influence of National Security Agengy NSA. |
SYSTEM DESIGN
|
| Client: An entity, which gets service from cloud. It has large data files to be stored in the cloud and get back the data whenever it needed. Maintenance and computation can be performed by individual users or organizations which creates it. |
| Cloud Storage: An entity, which contains multiple user data. It is managed by Cloud Service Provider (CSP), has significant storage space and computation resource to maintain the clients’ data. One or more cloud server combines to provide services to particular user |
| Organization: Background and system model are summarized in Section 2. Section 3 presents the proposed Bilinear programming computation, Elliptic curve algorithm for Encryption/Decryption technique, Duality Theorem to verify the result for secure outsourcing are described, Finally, we conclude in Section 4. |
LITERATURE SURVEY
|
| Bilinear Programming outsourcing provides a complete outsourcing solution. It develops a problem transformation technique that enables customer to secretly transform original BLP into some arbitrary one while protecting sensitive input/output information. Before explaining the Bilinear programming computation in Section 3, this section describes the system model assumed throughout the paper. Section 2.1 explains the data storage in the cloud as discussed in the literature with ECDLP algorithm. Section 2.2 describe about BUILDING CUSTOMER TRUST IN CLOUD COMPUTING WITH TRANSPARENT SECURITY. Section 2.4 discusses about DIMENSION SECURITY IN CLOUD COMPUTING. Section 2.5 describes about SECURE AND PRACTICAL OUTSOURCING OF BILINEAR PROGRAMMING IN CLOUD COMPUTING. Treating the cloud as an intrinsically insecure computing platform from the viewpoint of the cloud customers. Design mechanisms that not only protect sensitive information by enabling computations with encrypted data, but also protect customers from malicious behaviors by enabling the validation of the computation result. Focusing on computing and optimization tasks, investigates secure outsourcing is widely applicable through bilinear programming (BLP) computations. Problem transformation technique that enables customer to secretly transform original BLP into some arbitrary one while protecting sensitive input/output information. Uses Duality Theorem and derive a set of necessary and sufficient condition for result verification. "elliptic curve discrete logarithm problem” or ECDLP to provides a complete encryption technique for secure computation outsourcing |
DOMAIN PARAMETERS
|
To use ECC all parties must agree on all the elements defining the elliptic curve, that is, the domain parameters of the scheme. The field is defined by p in the prime case and the pair of m and f in the binary case. The elliptic curve is defined by the constants a and b used in its defining equation. Finally, the cyclic subgroup is defined by its generator G. For cryptographic application the order of G, that is the smallest non-negative number n such that , 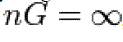 is normally prime. Since n is the size of a subgroup of is normally prime. Since n is the size of a subgroup of 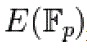 it follows from Lagrange’s theorem that the number it follows from Lagrange’s theorem that the number |
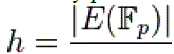 |
is an integer. In cryptographic applications this number h, called the cofactor, must be small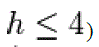 ) and, preferably, ) and, preferably,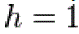 . Let us summarize: in the prime case the domain parameters are . Let us summarize: in the prime case the domain parameters are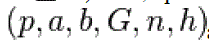 and in the binary case they are . and in the binary case they are .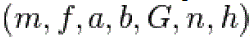 |
ENSURING DATA STORAGE SECURITY IN CLOUD COMPUTING
|
| Cloud computing has been envisioned as the next-generation architecture of IT enterprise. In contrast to traditional solutions, where the IT services are under proper physical, logical and personnel controls, cloud computing moves the application software and databases to the large data centers, where the management of the data and services may not be fully trustworthy. This unique attribute, however, poses many new security challenges which have not been well understood. In this article, we focus on cloud data storage security, which has always been an important aspect of quality of service. To ensure the correctness of users' data in the cloud, we propose an effective and flexible distributed scheme with two salient features, opposing to its predecessors. By utilizing the homomorphic token with distributed verification of erasure-coded data, our scheme achieves the integration of storage correctness insurance and data error localization, i.e., the identification of misbehaving server (s). Unlike most prior works, the new scheme further supports secure and efficient dynamic operations on data blocks, including: data update, delete and append. Extensive security and performance analysis shows that the proposed scheme is highly efficient and resilient against Byzantine failure, malicious data modification attack, and even server colluding attacks |
BUILDING CUSTOMER TRUST IN CLOUD COMPUTING WITH TRANSPARENT SECURITY
|
| Potential users of cloud services often fear that cloud providers’ governance is not yet mature enough to consistently and reliably protect their data. As the trend toward cloud-based services continues to grow, it has become clear that one of the key barriers to rapid adoption of enterprise cloud services is customer concern over data security (confidentiality, integrity, and availability). |
| It introduces the concept of transparent security and makes the case that the intelligent disclosure of security design, practices, and procedures can help improve customer confidence while protecting critical security features and data, thereby improving overall governance. Readers will learn how transparent security can help prospective cloud computing customers make informed decisions based on clear facts. For the purpose of discussion and debate, a model leveraging the series standards is presented as a commonly understood framework for disclosure. |
DIMENSION SECURITY IN CLOUD COMPUTING
|
| Cloud computing is emerging field because of its performance, high availability, least cost and many others. Besides this companies are binding there business from cloud computing because the fear of data leakage. Due lack of proper security control policy and weakness in safeguard which lead to many vulnerability in cloud computing. It has been written to focus on the problem of data leakage and proposes a framework works in two phases. First phase which is known as Data classification is done by client before storing the data. During this phase the data is to be categorized on the basis of CIA (Confidentiality, Integrity, and Availability). The client who wants to send the data for storage needs to give the value of C (confidentiality), I (integrity), A(Availability). The value of C is based on level of secrecy at each junction of data processing and prevents unauthorized disclosure, value of I based on how much assurance of accuracy is provided, reliability of information and unauthorized modification is required, and value of A is based on how frequently it is accessible. |
| With the help of proposed formula, the priority rating is calculated. Accordingly data having the higher rating is considered to be critical and 3D security is recommended on that data. After completion of first phase the data which is received by cloud provider for storage, uses 3Dimentional technique for accessibility. The sensitive proved data will send for storage to cloud provider. According to the concept of 3D user who wants to access the data need to be authenticated, to avoid impersonation and data leakage. |
| Now there is third entity who is either company’s (whose data is stored) employee or customer who want to access, they need to register first and then before every access to data, his/her identity is authenticated for authorization. |
KEY BASE AND SECURE DATA OUTSOURCING IN CLOUD COMPUTING
|
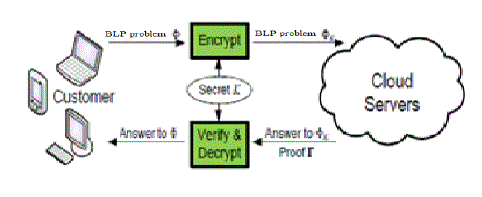
| Cloud Computing has great potential of providing robust computational power to the society at reduced cost .It enables customers with limited computational resources to outsource their large computation workloads to the cloud, and economically enjoy the massive computational power, bandwidth, storage, and even appropriate software that can be shared in a pay-per-use manner. Design mechanisms that not only protect sensitive information by enabling computations with encrypted data, but also protect customers from malicious behaviors by enabling the validation of the computation result. In order to achieve practical efficiency, our mechanism design explicitly decomposes the BLP computation outsourcing into public BLP solvers running on the cloud and private BLP parameters owned by the customer. The resulting flexibility allows us to explore appropriate security/efficiency tradeoff via higher-level abstraction of BLP computations than the general circuit representation. In particular, by formulating private data owned by the customer for BLP problem as a set of matrices and vectors, we are able to develop a set of efficient privacy-preserving problem transformation techniques, which allow customers to transform original BLP problem into some arbitrary one while protecting sensitive input/output information. To validate the computation result, we further explore the fundamental duality theorem of BLP computation and derive the necessary and sufficient conditions that correct result must satisfy. Such result verification mechanism is extremely efficient and includes close-to-zero additional cost on both cloud server and customers. Extensive security analysis and experiment results show the immediate practicability of our mechanism design. Such a mechanism of general secure computation outsourcing was recently shown to be feasible in theory, but to design mechanisms that are practically efficient remains a very challenging problem. |
LINEAR PROGRAMMING COMPUTATION
|
| In cloud computing outsourcing security was primary hindrance. There are numerous security issues for cloud computing as it encompasses many technologies including networks, databases, operating systems, virtualization, resource scheduling, transaction management, load balancing, concurrency control and memory management. Therefore, security issues for many of these systems and technologies are applicable to cloud computing. For example, the network that interconnects the systems in a cloud has to be secure. Furthermore, virtualization paradigm in cloud computing results in several security concerns. For example, mapping the virtual machines to the physical machines has to be carried out securely. Data security involves encrypting the data as well as ensuring that appropriate policies are enforced for data sharing. In addition, resource allocation and memory management algorithms have to be secure. Finally, data mining techniques may be applicable to malware detection in clouds. We have extended the technologies and concepts we have developed for secure grid to a secure cloud. We have defined a layered framework for assured cloud computing consisting of the secure virtual machine layer, secure cloud storage layer, secure cloud data layer, and the secure virtual network monitor layer. Due to the dynamic nature of cloud environments and the distributed nature of data, it is necessary to have a comprehensive security framework based upon security control objectives that are flexible and responsive to one’s particular security and compliance requirements. These security control objectives, when used within the context of a cloud environment, allow one to manage risk, implement compensating control, and address compliance requirements. Collectively, these allow customers to create a path to certification that will establish a level of assurance appropriate to a particular environment. An optimization problem is usually formulated as a mathematical programming problem that seeks the values for a set of decision variables to minimize (ormaximize) an objective function representing the cost subject to a set of constraints. For bilinear programming, the objective function is an affine function of the decision variables, and the constraints are a system of bilinear equations and inequalities. Since a constraint in the form of a bilinear inequality can be expressed as a linear equation by introducing a nonnegative slack variable, and a free decision variable can be expressed as the difference of two non-negative auxiliary variables, any bilinear programming problem can be expressed in the following standard form, minimize cT x subject to Ax = b; x _ 0: (1)Here x is an n _ 1 vector of decision variables, A is an m _ n matrix, c is an n _ 1 column vector, and b is an m _ 1 column vector. It can be assumed further that m _ n and that A has full row rank; otherwise, extras rows can always be eliminated from A. |
| An elliptic curve discrete logarithm problem refers to an algorithm that uses some kind of intractability in the definition of the method, and in the literature, may be called a lenstra elliptic curve factorization or lagrange’s algorithm, It ensure the Key generation for Encrypting the BLP Problem for customer to the cloud server. |
CONCLUSIONS AND FUTURE WORK
|
| This project work proposes on secure computation outsourcing using Bilinear Programming computation. Implementation of elliptic curve discrete logarithm problem or ECDLP to ensure a result of secure computation outsourcing and Uses Duality Theorem (DT) and derive a set of necessary and sufficient condition for result verification. Bilinear programming computation estimates the bandwidth for uploading the files in the cloud server and also determines the space availability in the server to furnish secure computation for outsourcing. Detecting the unfaithful behaviors for computation outsourcing is not an easy task, even without consideration of input/output privacy. Verifiable computation delegation, where a computationally weak customer can verify the correctness of the delegated computation results from a powerful but un trusted server without investing too much resources, has found great interests in theoretical computer science community. 1)devise robust algorithms to achieve concurrent programming; 2) explore the sparsity structure of problem for further efficiency improvement; 3) establish formal security framework; 4) extend our result to a big data server-storage on outsourcing in cloud. |
Figures at a glance
|
 |
| Figure 1 |
|
References
|
- N. Koblitz. Elliptic curve cryptosystems. Mathematics of Computation, 48:203–209, 1987.
- RSA Laboratory: FAQ. http://www.rsa.com/rsalabs/node.asp?id=2325
- SaikatBasu, A New Parallel Window-Based Implementation of the Elliptic Curve Point Multiplication in Multi-Core Architectures, International Journal of Network Security, Vol. 13, No. 3, 2011.
- The Case for Elliptic Curve Cryptography, National Security Agency
|