Keywords
|
| Hierarchical clustering, Batch Updating, Feature selection, MapReduce, Bigdata |
INTRODUCTION
|
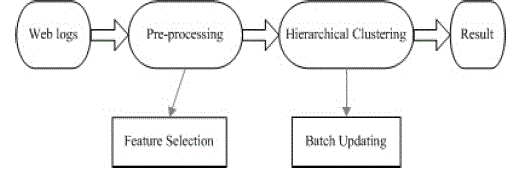
| MapReduce is the most popular cloud computing programming model nowadays. It provides programmers with powerful APIs by encapsulating the details of parallelism, fault tolerance and load balancing. So programmers with no parallel programming experience can write efficient parallel programs based on the model. Typical MapReduce programs run on large clusters. But the reality is most organizations can’t afford to build a large cluster. So building a small cluster to improve the efficiency of time-consuming applications is an economical and efficient solution. Non-data-intensive applications are common, which have small input data sets. But it takes long time to process the data sets, even a single record in it. Internet services such as e-commerce sites generate a large volume of web logs every day. The logs from millions of users provide a potential golden mine for understanding user access pattern and promoting new service value. But the large datasets also pose new challenges for data mining algorithms to efficiently process within given constraints such as memory and execution time. To overcome the constraints, data mining algorithms can be implemented with Map- Reduce[1], which breaks the large datasets into small chunks and process them in parallel on multiple cluster nodes and scales easily to mine hundreds of terabytes data[2] by adding inexpensive commodity computers. This paper explores the efficiency implementation of hierarchical clustering [3] with Map-Reduce, in the context of grouping Internet users based on web logs. In the application, the Internet users are grouped based on the keywords in title and meta information of web pages that users have accessed to. As a general framework, Map-Reduce provide good scalability but ignores the efficiency optimization of data mining algorithms. As a consequence, it takes nearly 80 hours to finish the mining job for the web logs of 1.2 terabytes involving nearly 1,000,000 users and 100,000 keywords. In contrast, the proposed improved hierarchical clustering method can accomplished the same task in nearly 6 hours Hierarchical clustering for large datasets consists of a large number of successive iterations of clustering processes, in which feature matrix merging and updating, similarity value modification are common operations. The matrix updating and similarity value modification invoke file operations of distributed file system and constant IO operations, which incur high IO and distributed node communication overhead. In addition, the large dimension of feature vectors demands high memory usages and causes heavy memory paging penalty. |
| In this paper, we present an efficient hierarchical clustering method for large datasets with Map-Reduce. We propose two optimization techniques to address the efficiency issues, which are believed to be applicable to other data mining algorithms implemented with Map-Reduce. We propose a Co-occurrence based feature selection technique at the preprocessing stage that takes the co-occurrence frequency as a contribution to the element value of feature vectors and makes, for each user, top N keywords with highest value as the selected features. Experiment shows the feature selection reduces the dimension of feature vectors to 49%, but with better accuracy of similarity values for user groups. |
| We approach Batch Updating to reduce the IO overhead and distributed communication cost during the clustering. The technique batches as many IO and communications operations as possible in one iteration, while assures the correctness of hierarchical clustering. We propose the in-memory batch updating principle that treats the top N pairs of user groups with highest similarity values in three different ways. The empirical study shows Batch Updating reduces the number of updating iterations to 6.01%, the clustering is accomplished in 7.45% of the original execution time. |
CO-OCCURRENCE BASED FEATURE SELECTION
|
| One method to improve efficiency of the hierarchical clustering is to reduce the dimension of user-keyword matrix. In this paper we propose co-occurrence based feature selection, motivated by the observations as follows. Firstly, the list of keywords extracted from the title and the keyword meta information are not equally important in weight and even some of them are noisy keywords. Secondly, the summary of a web page can be described by several keywords that are semantically related. For example, a page with title ”Apple iMac The all-in-one desktop for your photos, movie and music” can be summarized with the subset of keywords ”Apple iMac photos movie music”. Thirdly, semantically related keywords are more representative for the web page topic than other keywords. For instance in last example, ”apple”, semantically related to ”iMac”, is more representative than ”desktop”, though they both appear in the title. Co-occurrence based feature selection reduces the dimension of feature vectors by summarizing a user’s interested topics with the most representative keywords. For any two keywords, their co-occurrence frequency are calculated to reflect the relationship in semantics between keywords, and higher element value dmj (also called attention degree) of feature vectors is given to more related keywords than the others. Essentially the element value dmj consists of the contributions of both the number of keyword occurrences and the co-occurrence frequency of the pairs of keywords. The whole procedure of feature selection is performed in 5 phases, and is realized with 17 Map-Reduce tasks. The reduced user-keyword matrix is reused in a large number of clustering iterations, making the overhead of co-occurrence based feature selection amortized. |
A. Calculation of Attention degree for keywords
|
| Phase 1: the calculation of attention degree starts with counting the keywords and the pairs of keywords in title and the keyword meta information of web pages a user has visited. For every page title, this phase outputs Result1 and Result2 in following format: |
| R1 :< userm; keywordi; ni > |
| R2 :< userm; keywordi; keywordj ; nij > |
| R1 describes that keyword appears n times in the page accessed by userm; R2 describes that the pair keywordi and keywordj ) co-occurs nij times visited by userm.From the keyword meta information, the result set Result3 in format R3 are yield , describing that pair (keywordi and keywordj ) appeared nm ij times in meta information of urls. |
| R3 :< urls; keywordi; keywordj ; nm ij > |
| Our mining application pre-processes the raw data and outputs a matrix of near 1,000,000 users and 100,000 keywords. The large datasets take a long time to pre process, and operations on the generated matrix cannot be loaded into memory for efficient processing, and results in high IO and distributed communication overhead. |
| B. Feature selection |
| Feature selection and builds the reduced user-keyword matrix of low-dimension feature vector. Given the feature vector for a Internet user, we reduce the dimension by only keeping the top N attention degrees that are most representative for the users’ interested topics. |
| The final feature vectors are calculated in the following Steps: (1) Select the representative keywords for users. For each user, the accessed keywords are ranked in descending order of the final attention degrees, and the top N keywords are selected as representations of the user’s interests. (2) Union the all users’ representative keywords to form the final list of the selected features. (3) Obtain the feature vectors for the users based on the final list of selected features. Using result set Result as input, the element for keywords not in selected features are removed, and the userm’s attention degree dmi for keywordi in the selected features is set to the final attention degree dmi. If the dimension of the feature vector with selected features is m, and the number of users is n, the user-keyword matrix is given in formula (4), where each row is a feature vector for a user and the element value is the attention degree of the user for a keyword.co-occurrence based feature selection reduces the dimension of feature vectors to nearly a half, but with better accuracy of similarity values for user groups. |
MAPREDUCE PROGRAMMING MODEL
|
| The key of MapReduce programming model is map phrase and reduce phrase. Original input data is mapped into intermediate key/value pairs by many parallel map operations at map phrase. Many reduce operations are executed inparallel to produce the final results[4]. Map operation, which is written by users, takes original input data split as input and produces a group of intermediate key/value pairs. MapReduce framework collects these pairs, groups them by keys and passes them to reduce operation. Reduce operation, which is also written by users, takes the output of map phrase as input, merges these key/value pairs by key and produces final results. Usually each reduce operation produces a result. |
SOURCE OF DATA
|
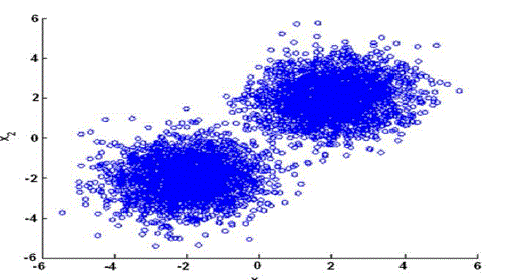
| We perform all experiments on 24 cluster nodes, which are Dell Power Edge 2950 servers with two dual-core processors (Intel Xeon 2.66GHz), 8GB RAM, and installed with Linux RHEL4. The nodes are connected by Gigabit Ethernet cable. The large datasets are the 1.2 TB web logs collected in six months, which contains more than 1,000,900 users, and the accessed keywords number 108,489.Therefore, the first two dimensions of the data are informative features that reveal the clustering structure, as shown in Fig.2, while the other features are random noises artificially added to test algorithm robustness. |
METHODOLOGY
|
| Generally, the hierarchical clustering consists of a large number of successive clustering iterations. Every iteration begins with calculating the similarity of every pair of user groups (or users) and finding out the most similar user groups, then merges them and updates the feature vectors in user-keyword matrix file. The direct parallelization of hierarchical clustering has the problem of causing poor performance: a large number of successive clustering iterations will incur high IO and distributed communication overhead due to the read/write operations both on disks and distributed file system, caused by both matrix updating and similarity value modification. |
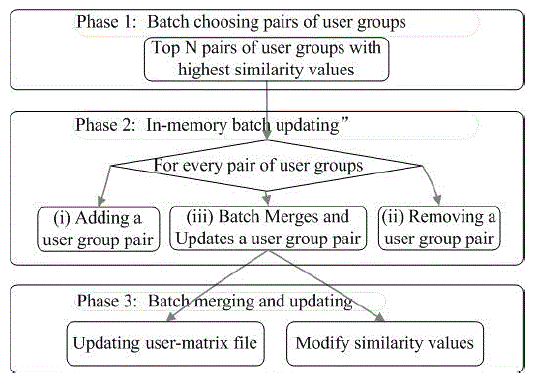
| This section details Batch Updating that is proposed to improve efficiency of hierarchical clustering for large datasets. The idea behind is to combine several iterations of clustering into one so that the updating matrix file and modifying similarity values are processed in batch mode, resulting in a shorter response time for the mining application. Fig.3 illustrates three major phases of the hierarchical clustering with Batch Updating. Phase 1 batch chooses the top N pairs of user groups for the iteration of clustering, Phase 2 performs in-memory batch updating on the chosen user groups as many as possible; Phase 3 updates the user keyword matrix file and similarity values, both being stored in distributed file system. |
A. Data structures
|
| The improved hierarchical clustering methods use two new data structures for efficient clustering. (1) C-queue: a queue that stores top N pairs of user groups with highest similarity values. The element in the queue is Cij , which denotes the pair contains user groups ui and uj. All elements in C-queue are sorted in descending order. Without loss of generality, we make the following assumption for the element Cij : (i¡j). |
| (2) Batch-queue: a queue that stores Cij (i¡j) to be batch processed in one iteration. In fact, the pairs in C-queue are processed in queue order one by one and are inserted into Batch-queue if necessary. Therefore, elements in Batch queue are also sorted in order. |
B. In-memory batch updating Principle
|
| The principle behind in-memory batch updating is to batch process as many iterations of user group clustering as possible, so long as no wrong clustered user groups are generated. To guarantee the correctness of the clustering, an element in C-queue is processed in three different ways: (a) Insert the element into Batch-queue; or (b) ignore the element by Batch-queue; or (c) end the iteration of batch updating by merging and updating of the pairs in Batch queue. Assume Batch-queue contains m elements, three different ways of processing the element Cij in C-queue and the rationale behind are described as follows. Insert Cij into Batch-queue. The process takes place when no elements exist in Batch-queue that have user groups equal to the user group ui or uj that Cij denotes, as formally defined as follows: |
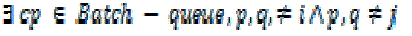 |
| The reason for this is that, the processing including user keyword matrix and similarity value updating for the elements in Batch-queue has no side-effects on the processing of the element Cij . As a result, the element is directly inserted into Batch-queue. |
| (b) Ignoring Cij . As long as there exists an element Cpq in Batch-queue that uq is the same as one of the user groups denoting by Cij , Cij can be removed from C-queue and ignored by Batch-queue. The condition is formally given by formula. |
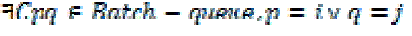 |
| Hierarchical clustering contains the process of merging user groups, which means, after processing the element Cpq (p<q), the user groups up and uq are merged. In our merge strategy, we only keep the user group up and replace its feature vector with updated element values using , and the user group uq disappears. As the element Cij meets , we just remove it from C-queue and start processing the next element. |
| (c) Merge and update the pairs in Batch-queue. It is taken when there exists an element Cpq in Batch-queue that the user group up is same as ui or uj . Formally the condition is given as follows: |
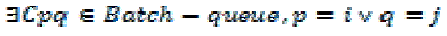 |
| The reason is that, Cij is at the head of C-queue in advance. If we update the feature vector of user and modify the similarity values, the similarity values of the element Cij and other elements in C-queue may be changed as well as the order of elements in C-queue, which means Cij is probably not at the head of C-queue. Therefore, we need to batch merge the clusters, update user-keyword matrix and modify similarity values by the elements in Batch-queue, then start a new batch updating, based on the up-to-date similarity values. |
MAPREDUCE
|
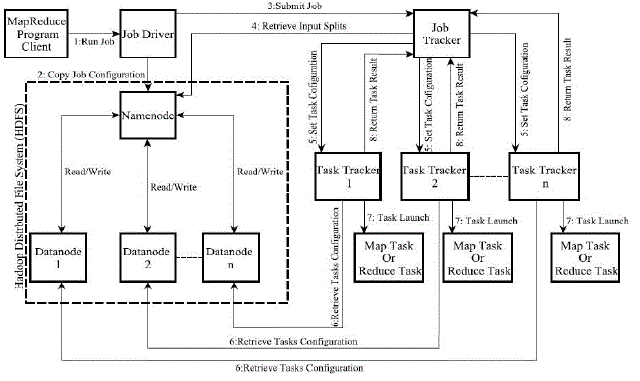
| A MapReduce program is composed of a Map() procedure that performs filtering and sorting (such as sorting students by first name into queues, one queue for each name) and a Reduce() procedure that performs a summary operation (such as counting the number of students in each queue, yielding name frequencies). The "MapReduce System" (also called "infrastructure", "framework") orchestrates by marshalling the distributed servers, running the various tasks in Hierarchical, managing all communications and data transfers between the various parts of the system, providing for redundancy and fault tolerance, and overall management of the whole process. 'MapReduce' is a framework for processing problems across huge datasets using a large number of computers (nodes), collectively referred to as a cluster (if all nodes are on the same local network and use similar hardware) or a grid (if the nodes are shared across geographically and administratively distributed systems, and use more heterogeneous hardware). MapReduce can take advantage of locality of data, processing data on or near the storage assets to decrease transmission of data. |
A.Row Cluster Re-assignment
|
| Map function. The input to the Map function is a (tuple id,entry tuple) pair. The Map function computes the distance of the entry Zij from each of the k possible row clusters that row i could be assigned to. The row id and an entry distance tuple (consisting of the matrix entry tuple augmented with the vector of k distances) are output as the intermediate key and value, respectively. Reduce function. The input to the Reduce function is a row id and the list of values (entry-distance tuples) for the entries in the corresponding row. The Reduce function simply sums up the distances of the individual row elements to find the total distance of the row from k possible row clusters. The row is then assigned to the row cluster with the minimum distance. The entry tuples are updated with the new row cluster assignment and pairs of tuple ids and entry tuples (without distance vectors) are output. |
B. Implementation with Map-Reduce
|
| Our hierarchical clustering using 3 Map-Reduce tasks for batch choosing pairs of user groups (phase 1), updating the user-keyword matrix file (phase3) and modifying the similarity value file (phase 3) Respectively. The in-memory batch updating (phase 2) involves processing elements in C-queue as well as filling them into Batch-Queue, both of which are directly performed at the master node. |
C. Feature selection evaluation
|
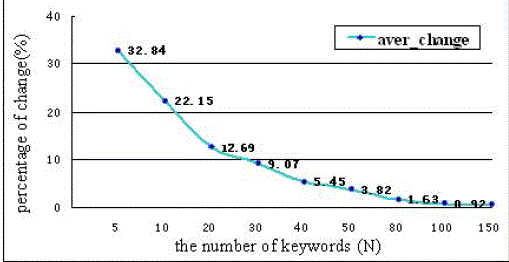
| Co-occurrence based feature selection uses a subset of keywords as features to reduce the dimensions of both feature vectors and user-keyword matrix. We build the user keyword matrix with and without feature selection. Table.1 lists the changes of keyword numbers, where N=100 top keywords are selected for each user. The dimension of the matrix and the feature vectors is reduced to 49%, from 108,489 to 53,049. As most feature vectors are sparse, memory requirement is decreased and similarity calculation is more efficient. Feature selection changes the attention degrees of the keywords accessed by users. We measure the changes of top N keywords for the users using metrics given as (10) and (11), which measures the changes of top interested keywords for a single user ui and the global average changes for all the users respectively. |
| Where Mij is an indicator variable for the changes. Mij=1,if keyword , one of the user Ui selected features, is not one of the original top N keywords without feature selection, otherwise Mij=0. Figure 3 shows the average change ratio with the different choice of parameter N. The change ratio of top keywords decrease as number of selected keywords for each user grows. We choose N=100 for feature selection as it results in low average change percentage (0.92%). |
D.Batch Updating evaluation
|
| We first evaluate the efficiency of hierarchical clustering with Batch Updating under different size N of C-queue. The size N affects how many pairs of user groups are batch choose and results in changing the total execution time. Table 2.shows the numbers of iterations and the total execution times with the different N, which implies the iteration numbers are approximately equal(they are affected by the condition that some critical values are equal) and the bigger N does not necessarily mean more efficient clustering. |
| Then we evaluate the efficiency improvement of hierarchical clustering with Batch Updating. We choose the size of Cqueue as N=50, and Table.3 shows the comparison results of hierarchical clustering for the large datasets. The results show that Batch Updating decreases the total execution time of our mining application to 7.45%. The major efficiency contribution is the reduced IO operations and communication costs, incurred by the only 6.02% iterations of hierarchical clustering with Batch Updating. |
RELATED WORK
|
| Hierarchical clustering, has become increasingly popular in recent years as an effective strategy for tackling large scale data clustering problems. There are Hierarchical k-means [7] Parallel clustering [8], Hierarchical MST [9], Hierarchical mean-shift [10], and Hierarchical DBSCAN [11], to name a few. |
| In terms of the Hierarchical programming framework used for Hierarchical clustering, a majority of Hierarchical clustering algorithms have been implemented using MPI, a message passing interface specification for Hierarchical programming [5]. More recently MapReduce [7], a Google Hierarchical computing framework and its Java version Hadoop have been increasingly used. For example, Hadoop k-means [8],and MapReduce hierarchical clustering. Hierarchical implementation of spectral clustering is most related to our study in this paper since power iterative clustering described in this paper is related to spectral clustering. In their work they started with approximating the dense similarity matrix by sparsifying it. They then used MapReduce as the Hierarchical computing framework to construct the sparse similarity matrix using t-nearest neighbours. For eigen decomposition, they used a Hierarchical eigen solver package called PARPACK, a Hierarchical ARPACK implementation based on MPI. Our work is on the Hierarchical implementation of power iteration clustering. |
CONCLUSION AND FUTURE DIRECTIONS
|
| This paper explores the efficient implementation of hierarchical clustering algorithms with Map-Reduce, in the context of grouping Internet users based on web logs. To reduce the memory requirement for the large size of features, Co-occurrence based feature selection technique is proposed. We also proposed a new fully distributed architecture to implement the MapReduce programming model. Nodes pull for job assignments and global status in order to determine their individual actions. The architecture also uses queues to shuffle results from Map to Reduce. Even though a full scale performance evaluation is beyond the scope of this paper, our preliminary results indicate the is a practical system and its performance is on par with that of Hadoop. Our experimental results also indicate that using queues to overlap the map and shuffling stage seems to be a promising approach to improve MapReduce performance. To lower the IO and distributed communication overhead, we propose Batch Updating to combine as many user groups merging and updating as possible in one update iteration. For the future work, we plan to further investigate miscellaneous variations of sequential pattern mining on hybrid cloud environment. |
Tables at a glance
|
|
|
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 5 |
Figure 6 |
|
References
|
- J. Dean and S. Ghemawat. MapReduce: Simpilifed Data Processing on Large Clusters, In Communications of ACM, 51(1),107-113,2008.
- Yahoo! Launches World’s Largest Hadoop Production Application, http://tinyurl.com/2hgzv7.
- A.Jain,M.Murty, and P.Flynn. Data Clustering: A Review. In ACM Computing Surveys, 31(3), 1999.
- J.L.Rodgers,andW.A.Nicewander.Thirteen ways to look at the correlation coefficient. The American Statistician 42, 59-66,1988.
- D. Lewis, and R. Marc. A comparison of two learning algorithms for text categorization.in SADIR,1994, pp.81-93.
- G. Xiubo, T. Liu, T. Qin, and H. Li. Feature selection for ranking. In Proc. SIGIR. 2007, Pp. 407-414.
- Weizhong Yana, UmangBrahmakshatriya a, YaXuea, Mark Gilder b, Bowden Wisec July (2012), “p-PIC: Parallel power iteration clustering forbigdata”, Elsevier on J. Hierarchical Distrib. Computing, pp. 352-359.
- V. Olman, F. Mao, H. Wu, Y. Xu,(2009). Hierarchical clustering algorithm for large data sets with applications in bioinformatics, IEEE Transactions onComputational Biology and Bioinformatics 6 (2),pp. 344–352.
- H. Wang, J. Zhao, H. Li, J. Wang, (2011). Hierarchical clustering algorithms for image processing on multi-core CPUs, in: 2008 InternationalConference on Computer Science and Software Engineering.
- Z. Du, F. Lin(2005), A novel Hierarchicalization approach for hierarchical clustering, Hierarchical Computing 31,pp.523–527.
- A. Cuzzocrea, Il-Y. Song, K.C. Davis (2011), Analytics over large-scale multidimensional data: the big data revolution! in: Proceedings ofDOLAP,pp.101–104.
- R. T. Ng, and J. Han. Efficient and Effective Clustering Method for spatial Data Mining. In proc. Of VLDB, 1994.
|