Enhancing the Performance of Mining High
Utility Itemsets Based On Pattern Algorithm

Ranjith Kumar. M; kalaivani. A; Dr. Sankar Ram. N

Enhancing the Performance of Mining High Utility Itemsets Based On Pattern Algorithm

Ranjith Kumar. M¹, kalaivani. A², Dr. Sankar Ram. N³

Assistant Professor, Dept. of CSE., R.M. K College of Engineering and technology, Chennai, India
Assistant Professor, Dept. of CSE., R.M. K College of Engineering and technology, Chennai, India
Professor, Dept. of CSE., R.M. K College of Engineering and technology, Chennai, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Data Mining is the process of analyzing data from different perspectives and summarizing it into useful information. An association in data mining indicates a logical dependency between various attributes of an entity. Association rule mining (ARM) is the process of mining past data for association rules. ARM only find the frequency of itemsets, which will not provide large amount of profit. Utility mining focuses on discovering the itemsets with high sales profit. Here, utility mining is a measure of profitability of items to the users. The utility mining of itemsets is an important task in decision-making process of many applications such as website click streaming analysis, cross marketing in retail stores and in biomedical applications. The extraction of the high utility itemsets from a large database involves the creation of new candidate itemsets with high utility. This affects the performance of the mining process in terms of the execution time and the space requirement.

Keywords

Utility Mining, High-utility itemsets, Rare itemsets, Frequent Itemset mining

INTRODUCTION TO UTILITY MINING

INTRODUCTION

Data Mining is an area that deals with ‘Knowledge Discovery’ from databases. It deals with analyzing data from different perspectives and summarizing it into useful information that can be used to increase revenue, cuts costs, or both. It also deals with extracting hidden patterns from the data available and converting this data into knowledge. Data mining can be applied to data sets of any size and is commonly used in a wide range of applications, such as marketing, fraud detection and scientific discovery. In areas such as marketing, data mining techniques are used to study customerbuying patterns to device marketing strategies. This can be done based on two criteria namely, the frequency which defines how often a product is sold and the utility which tells the profit associated with each product. Initially algorithms used for mining transaction databases focused on finding frequent item sets, but the importance of a product is measured mainly on the utility it gives on each transaction. This gives way to the methodology of Utility Mining.

Mining high utility itemsets from the databases refers to finding the itemsets with high utilities like profits. The basic meaning of utility is the importance/profitability of items to the users. The utility of items in a transaction database consists of two aspects: (1) the importance of the distinct item, which is called external utility, and (2) the importance of the items in the transaction, which is called internal utility. The utility of an itemset is defined as the external utility multiplied by internal utility. An itemset is called a high utility itemset if the utility is no less than the user specified threshold; otherwise, the itemset is called a low utility itemset.

Mining high utility itemsets from the database is not an easy task since the downward closure property used in frequent itemset mining cannot be applied here. In other words, pruning search space for high utility itemset mining is difficult because a superset of a low utility itemset may be a high utility itemset. An efficient approach for this problem is to enumerate all itemsets from the database by the principle of exhaustion. This approach will encounter the large search space problem, especially when database contain lot of long transaction. Hence, how to effectively prune the search space and efficiently capture all high utility itemsets with no miss is a big challenge in utility mining.

The traditional methods of utility mining were primarily concerned with the generation of all possible combination of item sets and then calculating the utility of the item sets. This was also known as Candidate Generation, where a candidate is a group of item sets. When the number of items is increased, the complexity becomes high.

There are many methodologies to mine High utility item sets from a transaction database. Though the most primitive methods made use of Candidate Generation, several methods were evolved to find the High utility item sets avoiding Candidate Generation. One such methodology is proposed here. The motivation for this project is from one such methodology. The project aims at reducing the candidate generation required for identifying the High utility item sets and thus reducing the number of database scan

LITERATURE SURVEY

INTRODUCTION

The concept of Utility mining deals with the isolation of High utility item sets from a transaction database. High utility item set mining is a research area of utility based descriptive data mining, aimed at finding item sets that contribute most to the total utility.

Algorithm such for mining frequent itemsets have been proposed earlier such as Apriori algorithm[1], FPgrowth algorithm[3]. Apriori algorithm is the initiative algorithm for efficient mining association rules from large databases. FP-Growth is a tree based approach, which provides better performance than Apriori based algorithm since it finds frequent itemsets without generating any candidate sets. In frequent itemset mining, the importance of items to users is not considered. The unit profits and purchased quantities of the items are not taken into considerations. Some methods were proposed for mining high utility itemsets from the databases such as UMining[6], Two-Phase[4], IIDS[5] and IHUP[8].

HIGH UTILITY PATTERN MINING

The theoretical model and definitions of high utility pattern mining were given in [9] proposed by H. Yao. This approach, called mining with expected utility (MEU). This approach is used to identify the high utility itemsets based on information in the transaction database and external information about utilities. MEU cannot maintain the downward closure property of Apriori and the authors of [9] used a heuristic to determine whether an itemset should be considered as a candidate itemset. Also, MEU usually overestimates, especially at the beginning stages, where the number of candidates approaches the number of all the combinations of items. This trait is impractical whenever the number of distinct items is large and the utility threshold is low.

UMINING ALGORITHM

A Unified Framework for Utility Based Measures for Mining Itemsets was proposed by Yao et al[6]. In this algorithm, a unified framework for incorporating several utility based measures into the data mining process by defining a unified utility function is proposed. The mathematical properties of utility based measures that will allow the time and space costs of the itemset mining algorithm to be reduced is summarized in this algorithm. Although it is shown to have good performance, it cannot capture the complete set of high utility itemsets since some high utility patterns may be pruned during the process.

TWO-PHASE ALGORITHM

Two-Phase algorithm proposed by Liu et al[4]. to efficiently prune down the number of candidates and can precisely obtain the complete set of high utility itemsets. It consist of two phases. In phase I, Two-Phase algorithm employs a breadth first search strategy to enumerate HTWUIs. It generates candidate itemsets of length k from HTWUIs of length (k-1) and prunes candidate itemsets by TWDC property. In each pass, HTWUIs and their estimated utility values i.e., TWUs, are computed by scanning database. After that, the complete set of HTWUIs is collected in phase I. In phase II, high utility itemsets and their utilities are identified from the HTWUIs by scanning original database once. Although Two-Phase algorithm effectively reduces the search space by TWDC property and captures the complete set of high utility itemsets, it still generates too many candidates for HTWUIs and requires multiple database scans.

IIDS ALGORITHM

To overcome the problem in Two-Phase algorithm, Li et al proposed an Isolated items discarding strategy(IIDS)[5] for discovering high utility itemsets and to reduce the number of candidates and improve the performance. IIDS shows that itemset share mining problem can be directly converted to utility mining problem by replacing the frequent values of each items in a transaction by its total profit, i.e., multiplying the frequency value by its unit profit. By pruning isolated items during the level-wise search, the number of candidate itemsets for HTWUIs in phase I can be reduced effectively. However, this approach still scans database multiple times and uses a candidate generation-and-test scheme to find high utility itemsets

SYSTEM DESIGN

PROBLEM DEFINITION

Consider the tables given below. The Transaction Database (Table 1) provides the information about the consumption of each of the item sets. And the Utility table (Table 2) provides information about the user defined utility value of each of the items. Let I={i1, i2,….. im} be a set of items and D be a transaction Ti ∈ D is a subset of I. Each item ip (1 ≤ p ≤m) has a unit profit p(ip). An itemset X is a set of k distinct items {i1, i2, …, ik}, where ij 1≤ j ≤ k, and k is the length of X. An itemset with length k is called k-itemset. A transaction database D = {T1, T2,.,Tn} contains a set of transactions, and each transaction Tq (1 ≤ d ≤ n) has an unique identifier d, called TID.Each item ip in the transaction Tq is associated with a quantity q(ip, Tq), that is, the purchased number of ip in Tq.

Definition 1: Utility u(ip,Tq) is the quantitative measure of utility for item ip in transaction Tq defined by u(ip,Tq)= q(ip,Tq) × p(ip). For example, u({D},T2)= 2 × 1= 2.

Definition 2:The utility of an itemset X in transaction Tq, u(X, Tq), is defined by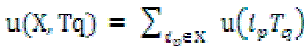

where X = {i1; i2; . . . . . . :ik} is a k-itemset, X ⊆Tq, and 1≤k ≤ m. For example, u({CD}, T1)= u({C}, T1) + u({D}, T1)= 1 + 2= 3.

The utility of an itemset X in D is defined by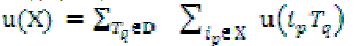

For example, u({AC}) = u({AC}, T1) + u({AC}, T2) + u({AC}, T3) = 6 + 16 + 6 = 28.

Definition 3:The transaction utility (tu) of transaction Tq denoted as tu(Tq) describes the total profit of that transaction In simple words, the transaction utility of a transaction is the sum of utilities of the individual items present in the transaction and is defined by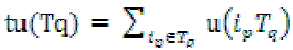

For example,tu(T1) = , u({A},T1)+ u({C},T1) + u({D},T1) = 5 + 1 + 2 = 8.

Definition 4:An itemset X is a high utility itemset if u(X) ≥ minutil. Finding high utility itemsets means determining all itemsets X having criteria u(X) ≥ minutil

Definition 5:Transaction-weighted utilization(TWU) of an itemset X, denoted by twu(X), is the sum of the transaction utilities of all transactions which contain the item set.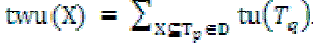

For example, twu({AC}) = tu(T1) + tu(T2) + tu(T3) = 8 + 27 + 30 = 65.

Definition 6:X is a high transaction-weighted utilization itemset (i.e., a candidate itemset) if twu(X)≥ minutil. For example, minutil= 40, twu({AC})=65, so twu({AC}) ≥40.

Definition 7:The transaction frequency (tf) of an item ip is tf(ip) and represents the number of transactions in which the item appears. The original frequency of ip is f(ip), which denotes the actual number of occurrences of ip in those transactions. For example, tf(C) = 5.

Definition 8: The transaction-weighted downward closure, which is abbreviated as TWDC, is stated as follows. For any itemset X, if X is not a HTWUI, any superset of X is a low utility itemset. By this definition, the downward closure property can be maintained by using transaction-weighted utilization. For example, in Table 1, any superset of {AD} is a low utility itemset since TWU({AD}) < min_util.

Proposed Data structure

We use a compact tree structure, to maintain the information of transactions and high utility itemsets. Elements in Tree construction:

Each node N includes 1. N.name- the item name of the node. 2. N.count - the support count of the node. 3. N.nuestimate utility value of the node. 4. N.parent- the parent node of the node, 5. N.hlink- node link which points to a node whose item name is the same as N.name. Header table is implemented for the traversal of Tree. Each entry in the header table is composed of an item name, an estimate utility value, and a link. The link points to the last occurrence of the node which has the same item as the entry in the Tree. By following the link in the header table and the nodes in Tree, the nodes whose item names are the same can be Traversed efficiently.

Removing global unpromising items during the construction of a global Tree

The construction of Tree can be performed with two scans of the original database. In the first scan of database, the transaction utility of each transaction is computed. At the same time, TWU of each single item is also accumulated. After scanning database once, items and their TWUs are obtained. By TWDC property, if the TWU of an item is less than minimum utility threshold, its supersets are unpromising to be high utility itemsets. An item ip is called a promising item if TWU(ip) ≥ min_util. Otherwise, the item is called an unpromising item After the first scan of database, promising items are organized in the header table in the descending order of TWU values. During the second scan of database, transactions are inserted into UP-Tree. Initially, the tree is created with a root R.

Tree can be constructed by using the steps given below.

Tree construction procedure

Step1 : Create a root node and assign it as null

Step2: For each transaction Ti in the Transaction Database, extract the first element in the transaction.

Step3 : Check if there exists a node for the element among the children of root.

Step 3.1 If yes, add to the transaction utility of the element, the transaction frequency of the element in the current transaction.

Step 3.1.1 Check the child of the node and the next element in the transaction

Step 3.1.2 If they match, repeat the process of adding to the transaction utility of the element, the utility in the particular transaction.

Step 3.2 If no, then create a new node and assign it as the child of the root and add the other elements in the transaction as the child of the newly created node.

This procedure when applied to the set of transactions in the transaction database, the tree is created. When a transaction is retrieved, unpromising items are removed from the transaction and their utilities are eliminated from the TU of the transaction since only the supersets of promising items are possible to be the high utility itemsets. The remaining promising items in the transaction are sorted in the descending order of TWU. The transaction after the above reorganization is called reorganized transaction and its TU is called RTU (reorganized transaction utility) shown in Table 3. The RTU of a reorganized transaction Td is denoted as RTU(Td).

Example 1: Consider the transaction database in Table 1 and the profit table in Table 2. Suppose the minimum utility threshold min_util is 40. In the first scan of database, TUs of the transactions and the TWUs of the items are computed. They are shown in the last column of Table 1 and in Table 4, respectively. From Table 4, {F} and {G} are unpromising items since their TWUs are less than min_util. The promising items are reorganized in the header table in the descending order of TWU. Table 3 shows the reorganized transactions and their RTUs for the database in Table 1. As shown in Table 3, unpromising items {F} and {G} are removed from the transactions T2, T3 and T5, respectively. Besides, the utilities of {F} and {G} are eliminated from the TUs of T2, T3 and T5, respectively. The remaining promising items {A}, {B}, {C}, {D} and {E} in the transaction are sorted in the descending order of TWU. Then, we insert reorganized transactions into the Tree by the same procedure as mentioned above.

Example 2 : Insertion operation. Consider the reorganized transactions in Table 4. The first reorganized transaction T1’ = {C, A, D} leads to create a branch in Tree. The node {C} is created under the root with {C}.count = 1 and {C}.nu = 8. The second node {A} is created under node {A} with {A}.count = 1 and {A}.nu = 8. The third node {C} is created as a child of node {A} with {C}.count =1 and {C}.nu = 8. When the next reorganized transaction T2’ = {C, E, A} is retrieved, the node utility of the node {C} is increased by 22 and {C}.count is increased by 1. Then, a new node {E} is created under {C} with {E}.count=1 and {E}.nu = 22. Similarly, a new node {A} is created under the node {E} with {A}.count=1 and {A}.nu = 22. The reorganized transactions T3’, T4’ and T5’ are inserted in the same way. The tree is constructed with inserting all reorganized transactions.

Generating HUIs from the Tree by applying FP-Growth

In Figure 1, each node in the Tree has two numbers: one is support count and another one is node utility. The nodes which have the same item names are linked in a sequence by their node links. In the Tree, each node {ai} to the root forms a path ({ai}-> {ai+1}-> ... -> {an}). Each path represents a prefix that is shared by multiple reorganized transactions. {ai}.count is the number of reorganized transactions that share the path and {ai}.nu is an estimate utility value for the path. Similar to [8], HUIs can be generated from the Tree by applying FP-Growth [3].

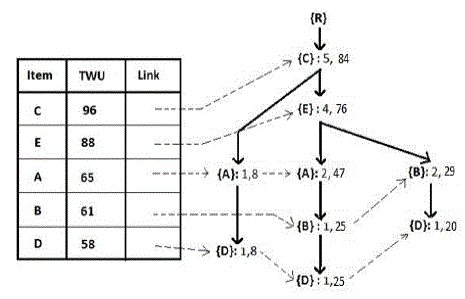
Example 3. Consider the Tree in Figure 2. Suppose min_util is 40. The algorithm starts from the bottom of the header table and considers the item {D} first. By applying FP-Growth, a HUI {D}:58 is generated since its estimate utility value, i.e., 58, is above than min_util. By following {D}.hlink, the nodes with the same item names are found. By tracing the nodes to root, three paths (D->A-> C: 1, 8), (D->B->A->E->C: 1, 25) and (D->B->E->C: 1, 20) are found. For each path, the first number beside the path is the support count and the second number is the path utility, which is equal to {D}.nu. These paths are collected into {D}’s conditional pattern base[3] which is denoted as {D}-CPB and shown in Table 5. In this table, the collected paths are shown in the first column; the support counts and the path utilities of the paths are shown in the third and the forth columns, respectively. For convenience, the path ({ai}- >{ai+1}->...->{an}) in the conditional pattern base is denoted as {ai, ai+1,..., an} and the item ai is discarded from the path in {ai}’s conditional pattern base since every path in {ai}-CPB must contain ai

Definition 9. (Path utility of a path in a conditional pattern base)

The path utility of a path pj = ({ai}->{ai+1}->...->{an}) in {ai}-CPB is equal to {ai}.nu and is denoted as pu(pj, {ai}- CPB). For example, in Table 5, the path utility of the path {AC} in {D}-CPB is 8.

Definition 10. (Path utility of an item in a path in a conditional pattern base)

For each item ip in the path pj in {ai}-CPB, the path utility of an item ip in a path pj in {ai}-CPB is equal to pu(pj, {ai}-CPB)and denoted as pu(ip, pj). For example, the path utility of {A} in the path {AC} is 8.

Definition 11. (Path utility of an item in a conditional pattern base)

The path utility of an item ip in {ai}-CPB is defined as ,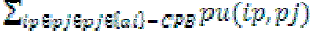

which is denoted as pu(ip, {ai}-CPB). For example, the path utility of item {A} in {D}-CPB is equal to (pu({A}, {AC}) + pu({A}, {BAEC})) = (8 + 25) = 33.

Definition 12. (Local promising item in a conditional pattern base)

An item ip is called a local promising item in {ai}-CPB if pu(ip, {ai}-CPB) ?? min_util; otherwise, ip is called a local unpromising item.

Example 4. By scanning {D}-CPB once, items and their path utilities are obtained, which is shown in Table 6. In Table 6, item {A} is a local unpromising item since its path utility is less than min_util, i.e., 33<40. Then, local promising items {B}, {C} and {E} are arranged in the local header table. Scan {D}-CPB again to construct {D}’s conditional UPTree [5], which is denoted as {D}-Tree. When a path in the conditional pattern base is retrieved, unpromising items are removed from the path and the remaining items are rearranged in the descending order according to their local path utilities. The reorganized paths are shown in the second column of Table 5. After inserting all reorganized paths, {D}- Tree is constructed completely and shown in Figure 4(a). Generating PHUIs from {D}-Tree by applying FP-Growth, a set of PHUIs which are involved with item {D} are obtained, that is, {{D}:58, {DE}:45, {DEB}:45, {DEC}:45, {DEBC}:45, {DB}:45, {DBC}:45, {DC}:53}. Consider the next item, i.e., {B}, in the global header table in the same manner, it derives a set of PHUIs which includes item {B}, that is, {{B}:61 {BE}:54, {BEC}:54, {BC}:54}. Consider the remaining items in the header table and we can obtain the rest PHUIs, i.e., {{A}:65, {AC}:55, {ACE}:47, {AE}:47, {E}:88, {EC}:76, {C}:96}. After finding all PHUIs high utility itemsets and their utilities are identified from the set of PHUIs by scanning original database once.

Removing node utilities in construction of Tree

As shown in example 5, the search space of high utility itemsets can be divided into five smaller search spaces: (1) {D}-CPB, (2) {B}-CPB without containing item {D}, (3) {A}-CPB without containing items {B} and {D}, (4) {E}- CPB without containing items {A}, {B} and {D}, and (5) {C}-CPB without containing items {E}, {A}, {B} and {D}. When DGU strategy is applied, there are two paths {AEC}: 25 and {EC}: 29 in {B}-CPB, where the numbers beside the paths are their path utilities. Although {D} doesn’t appear in {B}’s conditional pattern base, the utility of {D} is involved in the path utilities of the paths in {B}-CPB. The path utility of the path {AEC} is 25, which is equal to the RTU of the reorganized transaction T3’. This estimated utility value is actually the sum of u({B}, T3’), u({D}, T3’), u({A}, T3’), u({E}, T3’) and u({C}, T3’).

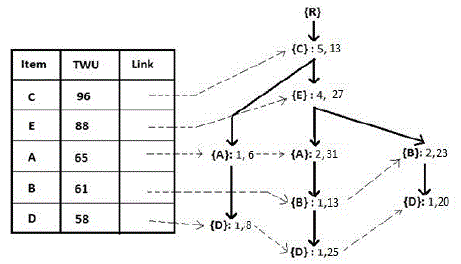
However, all paths in {B}-CPB are not related with {D} since {D} is below {B} in the UP-Tree as shown in Figure 2. Besides, only the item which is an ancestor of the node {B} will appear in {B}-CPB. Any item which is a descendant of the node {B} will not appear in {B}-CPB. Therefore, the utilities of {B}’s descendants can be removed from the path utility of each path in {B}-CPB. The process can be done during the construction of global UP-Tree since the paths in the conditional pattern bases are directly derived from the global UPTree. When a reorganized transaction tj’ = {i1, i2, …, in} (ik?I, 1 ≤ k ≤ n) is inserted into a global UP-Tree, the function Insert_Reorganized_Transaction(R, i1) is called The Insert_Reorganized_Transaction(N, ix) function takes a node N in the Tree and an item ix (ix?tj’, 1 ≤ x ≤ n) in the reorganized transaction tj’ as inputs.

Example 6. Consider the reorganized transactions in Table 4. When T1’ = {(C,1) (A,1) (D,1)} is inserted to a global UP-Tree, the first node {C} is created. {C}.nu is increased by the RTU of T1’ minus the utilities of the rest items which are behind the item {C} in T1’, i.e., {C}.nu = RTU(T1’) – ( u({A}, T1’) + u({D}, T1’) ) = 8 – (5+2) = 1. For convenience, it can also be considered as the sum of the utilities of the items which are before the item {D} in T1’, i.e., {C}.nu = p({C}) × q({C}, T1’) = 1×1 = 1, where p({C}) is the unit profit of the item {C} and q({C}, T1’) is the purchased number of {C} in T1’. The second node {A} is crated with {A}.count = 1 and {A}.nu = (p({C}) × q({C}, T1’) + p({A}) × q({A}, T1’)) = (1×1 + 5×1) = 6. The third node {D} is created with {D}.count = 1 and {D}.nu = (p({C}) × q({C}, T1’) + p({A}) ×q({A}, T1’) + p({D}) × q({D}, T1’)) = (1×1 + 5×1 + 1×2) = 8. When T2’ = {(C, 6) (E, 2) (A, 2)} is inserted into the tree, {C}.nu is increased by p({C}) × q({C}, T2’) = 6 and {C}.count is increased by 1. Then, a new node {E} is created under the node {C} with {E}.count = 1 and {E}.nu = 12. Similarly, a new node {A} is created under the node {E} with {A}.count = 1 and {A}.nu = 22. After inserting all reorganized transactions, the global UP-Tree is constructed completely. Figure 3 shows the global UP-Tree. By Figure 3, we can know that the node utility of each node is significantly reduced. Generating PHUIs from the UP-Tree by applying FP-Growth, and we obtain a set of PHUIs, that is, {{D}:58, {DE}:45, {DEB}:45, {DEBC}:45, {DEC}:45, {DB}:45, {DBC}:45, {DC}:53, {B}:61, {A}:65, {E}:88, {C}:96}

CONCLUSION

High utility itemsets mining from transaction databases is obtained. Tree structure is proposed for maintaining the information of high utility itemsets. Hence, high utility itemsets can be generated efficiently from this Tree with only two scans of the database. This enhances the mining performance in utility mining. In the experiments, both of synthetic and real datasets are used to evaluate the performance of our algorithm. The mining performance is enhanced significantly since both the search space and the number of candidates are effectively reduced by the proposed strategies. Mining performance increases, when the database contains lots of long transactions.

Tables at a glance


Table 1	Table 2	Table 3


Table 4	Table 5	Table 6

Figures at a glance


Figure 1	Figure 2

References

R. Agrawal and R. Srikant., “Fast algorithms for mining association rules” In Proc. of the 20th Int'l Conf. on Very Large Data Bases, pp. 487-499, 1994.

J.S. Park, M.S. Chen &P.S.Yu , “An Effective Hash Based Algorithm for Mining Association Rules” (Apriori Algorithm) In SIGMODConference, 1995.

J. Han, J. Pei , Y. Yin & R. Mao , “Mining Frequent Patterns without candidate generation” (FP-Tree Method) SIGMOD Conference, 2000.

Y. Liu, W. Liao, and A. Choudhary., “A fast high utility itemsets mining algorithm.” In Proc. of the Utility-Based Data Mining Workshop,2005.

“Y.-C. Li, J.-S. Yeh, and C.-C Chang., “Isolated items discarding strategy for discovering high utility itemsets” In Data & KnowledgeEngineering, Vol. 64, Issue 1, pp. 198-217, Jan., 2008.

H. Yao, H. J. Hamilton, L. Geng, “A unified framework for utility-based measures for mining itemsets” In Proc. of ACM SIGKDD 2ndWorkshop on Utility-Based Data Mining, pp. 28-37, USA, Aug., 2006.

Vincent S.Teng, Cheng-Wei Wu., “UP-Growth : An Efficient Algorithm for High Utility Itemset Mining”, In Proc. of the 16th ACM Int'l Conf.on knowledge discovery and data mining.

C. F. Ahmed, S. K. Tanbeer, B.-S. Jeong, and Y.-K. Lee. , “Efficient tree structures for high utility pattern mining in incremental databases” InIEEE Transactions on Knowledge and Data Engineering, Vol. 21, Issue 12, pp. 1708-1721,2009

H. Yao, H.J. Hamilton, and C.J. Butz., “A Foundational Approach to Mining Itemset Utilities from Databases,” in Proc. Fourth SIAM Int’lConf. Data Mining (SDM ’04), pp. 482-486, 2004.

J.-L. Koh and S.-F. Shieh,, “An Efficient Approach for Maintaining Association Rules Based on Adjusting FP-Tree Structures,” Proc. Ninth Int’l Conf. Database Systems for Advanced Applications.