Keywords
|
| Data mining, Logical decision trees, imbalanced data sets, ensemble classification |
INTRODUCTION
|
| Imbalanced class distributions are frequently encountered in real-world classification problems, arising from fraud detection, risk management, text classification, medical diagnosis, and many other domains. Such imbalanced class data sets differ from balanced class data sets not only in the skewness of class distributions, but also in the increased importance of the minority class. Despite their frequent occurrence and huge impact in day-to-day applications, the imbalance issue is not properly addressed by many standard machine-learning algorithms, because they assume either balanced class distributions or equal misclassification costs [1]. |
| Various approaches have been proposed to deal with imbalanced classes to cope with these issues, including over/under-sampling [2], [3], Synthetic Minority Oversampling Technique (SMOTE), cost-sensitive [4], modified kernel based, and active learning methods [5], [6]. Although these methods do somewhat alleviate the problem, they are often based on heuristics rather than on clear guidance. For instance, in the oversampling technique, the optimal oversampling ratio varies largely across data sets, and is usually determined through multiple cross validations or other heuristics. |
| Recent findings suggest that the class imbalance problem should be approached from multiple angles as well as using different evaluation metrics [7]. These findings show that the degree of imbalance is not the only factor hindering the learning process. Rather, the difficulties reside with various other factors such as overlapping classes, lack of representative data, and small disjuncts. Even worse, the effect of such factors becomes amplified when the distribution of classes is highly imbalanced [1]. |
| The decision tree learning method is one of the methods that are used for classification or diagnosis. As for many other machine learning methods, the learning in decision trees is done by using a data set of already classified instances to build a decision tree which will later be used as a classifier. The set of instances used to “train” the decision tree is called the training set. |
RELATED WORK
|
| In [1] authors the continuous expansion of data availability in many large-scale, complexes, and networked systems, such as surveillance, security, Internet, and finance, it becomes critical to advance the fundamental understanding of knowledge discovery and analysis from raw data to support decision-making processes. Although existing knowledge discovery and data engineering techniques have shown great success in many real-world applications, the problem of learning from imbalanced data (the imbalanced learning problem) is a relatively new challenge that has attracted growing attention from both academia and industry. In [2] authors used all reduction methods improved identification of small classes (20-30%), but the differences were insignificant. However, significant differences in accuracies, truepositive rates and true-negative rates obtained with the 3-nearest neighbor method and C4.5 from the reduced data favored Neighborhood Cleaning Rule (NCL). The results suggest that NCL is a useful method for improving the modeling of difficult small classes, and for building classifiers to identify these classes from the real-world data. In [3] discussed the study compares the performance of classifiers generated from unbalanced data sets with the performance of classifiers generated from balanced versions of the same data sets. This comparison allows us to isolate and quantify the effect that the training set’s class distribution has on learning and contrast the performance of the classifiers on the minority and majority classes. The second study assesses what distribution is "best" for training, with respect to two performance measures: classification accuracy and the area under the ROC curve (AUC). In [4] authors discussed the Support Vector Machines (SVM) have been extensively studied and have shown remarkable success in many applications. However the success of SVM is very limited when it is applied to the problem of learning from imbalanced datasets in which negative instances heavily outnumber the positive instances (e.g. in gene profiling and detecting credit card fraud). This paper discusses the factors behind this failure and explains why the common strategy of under-sampling the training data may not be the best choice for SVM. In [5] authors discussed the problem occurs when there are significantly less number of observations of the target concept. Various real-world classification tasks, such as medical diagnosis, text categorization and fraud detection suffer from this phenomenon. The standard machine learning algorithms yield better prediction performance with balanced datasets. In this paper, we demonstrate that active learning is capable of solving the class imbalance problem by providing the learner more balanced classes. In [6] authors considered the large, real-world inductive learning problems, the number of training examples often must be limited due to the costs associated with procuring, preparing, and storing the training examples and/or the computational costs associated with learning from them. In such circumstances, one question of practical importance is: if only n training examples can be selected, in what proportion should the classes be represented? In this article we help to answer this question by analyzing, for a fixed training-set size, the relationship between the class distribution of the training data and the performance of classification trees induced from these data. |
PROPOSED ALGORITHM
|
| A. Splitting Decision Trees |
| Decision tree learning is a common method used in data mining. Most of the commercial packages offer complex Tree classification algorithms, but they are very much expensive. Decision tree algorithms generate tree-structured classification rules, which are written in a form of conjunctions and disjunctions of feature values (or attribute values). These classification rules are constructed through |
| ? selecting the best splitting feature based on a certain criterion, |
| ? partitioning input data depending on the best splitting feature values, |
| ? Recursively repeating this process until certain stopping criteria are met. |
| The selected best splitting feature affects not only the current partition of input data, but also the subsequent best splitting features as it changes the sample distribution of the resulting partition. Thus, the best splitting feature selection is arguably the most significant step in decision tree building, and different names are given for decision trees that use different splitting criteria, for example, C4.5 and ID3 for Shannon entropy-based splitting criteria such as and Information Gain ratio and CART for the Gini impurity measure. |
| B. Bagging-Based Ensembles |
| The bagging consists in training different classifiers with bootstrapped replicas of the original training data-set. That is, a new data-set is formed to train each classifier by randomly drawing (with replacement) instances from the original data-set (usually, maintaining the original data-set size). |
| A bagging algorithm does not require re-computing any kind of weights; therefore, neither is necessary to adapt the weight update formula nor to change computations in the algorithm. In these methods, the key factor is the way to collect each bootstrap replica (Algorithm 1), that is, how the class imbalance problem is dealt to obtain a useful classifier in each iteration without forgetting the importance of the diversity. |
 |
| C. First-Order Logical Decision Trees |
| The first-order logical decision tress l is a keel database; a test in a node corresponds to checking whether a query ← C succeeds in l ^ LEAT (with Lift-Boosting Ensemble of α-Trees (LEAT) the background knowledge). Note that it is not sufficient to use for C the conjunction conj in the node itself. Since conj may share variables with nodes higher in the tree, C consists of several conjunctions that occur in the path from the root to the current node. Therefore, when an example is sorted to the left, C is updated by adding conj to it. When sorting an example to the right, C need not be updated: a failed test never introduces new variables. |
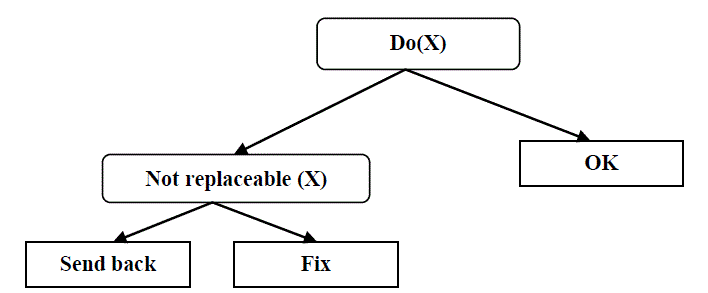
| A first-order logical decision tree (FOLDT) is a binary decision tree in which the nodes of the tree contain a conjunction of literals, and different nodes may share variables, under the following restriction: a variable that is introduced in a node (which means that it does not occur in higher nodes) must not occur in the right branch of that node. An example of a logical decision tree is shown in Fig. 1. It encodes the target hypothesis of Example 1. |
PSEUDO CODE
|
| Procedure Logical classify (s : sample) returns class: |
| Step 1: C := true |
| Step 2: N := root. |
| Step 3: while N ≠ leaf(c) do |
| Step 4: let N = inode(conj, left, right) |
| Step 5: if C ^ conj succeeds in Tree ^ s then |
| C := C ^ conj |
| N := left |
| else N := right |
| Step 8: return c |
SIMULATION RESULTS
|
| The simulation studies work has been evaluated the 20 data sets used in this paper are from the 1) KEEL Imbalanced Data Sets. Many of the KEEL data sets are derived from UCI Machine Learning Repository by either choosing imbalanced datasets, or collapsing/removing some classes to make them to imbalanced binary data sets. paw02a, 03subcl5, and 04clover are artificial data sets, which are not from the UCI repository. They are designed to simulate noisy, borderline, and imbalanced examples in [43]. Aside from the stated modifications, each data set from the KEEL Repository is used “as is.” |
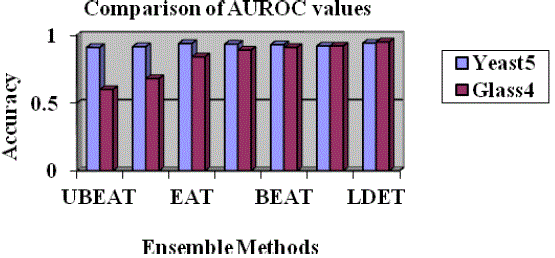
| Table 1 shows that logical decision tree classification, α-diversified classifiers using EAT framework: EAT (α - diversified single tree), BEAT (α -diversified bagged trees), and UBEAT (α -diversified under-bagged trees) when K = 3. Note that the EAT framework can be plugged into any bagging-based ensemble algorithms such as over-bagging. Along with the two baseline algorithms and a single C4.5, these six algorithms are applied to the data sets, and AUROCs from 5 × 2 cross validations are recorded. |
| The results show that α -diversified ensembles result in better AUROC performance than the corresponding baseline approaches |
CONCLUSION AND FUTURE WORK
|
| The simulation results showed that the proposed algorithm performs better with the existing semi-supervised clustering algorithms. The proposed work of a new ensemble framework of First-order Logical relationships called FOLR that consistently results in higher AUROC values over the class imbalanced data sets. The proposed work modifies traditional pruning rules in decision tree algorithms to directly reflect an evaluation metric based on conditions. The First order logical relationship tree is a good generalization for unobserved instance, only if the instances are described in terms of features that are correlated with the target concept. The Decision is provide a clear indication of which fields are most important for prediction or classification. |
| As the future work the system need to tested with a large amount of data sets and require further training and classification to solve the problem of the comparative sentences that expressed in different domains. |
Tables at a glance
|
 |
| Table 1 |
|
Figures at a glance
|
 |
 |
| Figure 1 |
Figure 2 |
|
References
|
- H. He and E.A. Garcia, “Learning from Imbalanced Data,” IEEETransactions on Knowledge and Data Engineering, vol. 21, no. 9, pp. 1263-1284, Sept.2009.
- J. Laurikkala, “Improving Identification of Difficult Small Classes by Balancing Class Distribution,” Proc. Eighth Conf. AI in Medicine inEurope: Artificial Intelligence Medicine, pp. 63-66, 2001.
- G. Weiss and F. Provost, “The Effect of Class Distribution on Classifier Learning: An Empirical Study,” technical report, Dept. of ComputerScience Rutgers, Univ., 2001.
- K. McCarthy, B. Zarbar, and G. Weiss, “Does Cost-Sensitive Learning Beat Sampling for Classifying Rare Classes?” Proc. Int’l WorkshopUtility-Based Data Mining, pp. 69-77, 2005.
- R. Akbani, S. Kwek, and N. Japkowicz, “Applying Support Vector Machines to Imbalanced Data Sets,” Proc. 15th European Conf. MachineLearning, 2004.
- S. Ertekin, J. Huang, and C.L. Giles, “Learning on the Border: Active Learning in Imbalanced Data Classification,” Proc. 30th Ann. Int’lACM SIGIR Conf., pp. 823-824, 2007.
- N. Japkowicz and S. Stephen, “The Class Imbalance Problem: A Systematic Study,” Intelligent Data Analysis, vol. 6, no. 5, pp. 429-449, 2002.
- K. Napierala, J. Stefanowski, and S. Wilk, “Learning from Imbalanced Data in Presence of Noisy and Borderline Examples,” Proc . SeventhInt’l Conf. Rough Sets and Current Trends in Computing, pp. 158-167, 2010.
|