Faculty of Management and Economics Sciences, Université de Parakou, Benin
Received date: 10/05/2016 Accepted date: 24/05/2016 Published date: 28/05/2016
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
Multivariate Processes, Kernel Density, Hellinger Distance, Linear Process, Parametric Estimation, Long Memory, Multivariate Processes
Let 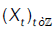 bead-variate linear process independent of the form:
bead-variate linear process independent of the form:
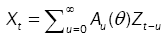 (1)
(1)
Defined on a probability space (Ω 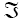 (F), p), where {Zt} is a sequence of stationary d-variate associated random vectors with
(F), p), where {Zt} is a sequence of stationary d-variate associated random vectors with 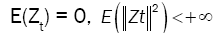 and positive definite covariance matrix ã: d×d . Throughout this paper we shall assume that
and positive definite covariance matrix ã: d×d . Throughout this paper we shall assume that
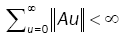 (2)
(2)
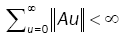 (3)
(3)
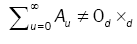
where for any d d, d = 2, matrix A = (aij(θ)) whose components depend on the parameter θ, such as 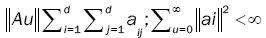 and 0d×d denotes the d×d zero matrix. Here θò Θ with Θ
and 0d×d denotes the d×d zero matrix. Here θò Θ with Θ 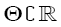 , with. Let
, with. Let
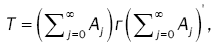 (4)
(4)
where the prime denotes transpose, and the matrix ÃÂó =(σkj) with
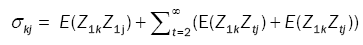 (5)
(5)
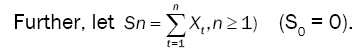
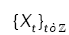 is assumed to be gaussian and have long rang dependent process. Fakhre-Zakeri and Lee proved a central theorem for multivariate linear processes generated by independent multivariate random vectors and Fakhre-Zakeri and Lee also derived a functional central limit theorem for multivariate linear processes generated by multivariate random vectors with martingale difference sequence. Tae-Sung Kim, Mi-HwaKo and Sung-Mo Chung [1] prove a central limit theorem for d-variate associated random vectors. The problem is how to estimate θ in order to investigate the fitting of the model to the data? An estimation of
is assumed to be gaussian and have long rang dependent process. Fakhre-Zakeri and Lee proved a central theorem for multivariate linear processes generated by independent multivariate random vectors and Fakhre-Zakeri and Lee also derived a functional central limit theorem for multivariate linear processes generated by multivariate random vectors with martingale difference sequence. Tae-Sung Kim, Mi-HwaKo and Sung-Mo Chung [1] prove a central limit theorem for d-variate associated random vectors. The problem is how to estimate θ in order to investigate the fitting of the model to the data? An estimation of 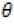 would have two essential properties: it would be efficient and its distribution would not be greatly pertubated.
would have two essential properties: it would be efficient and its distribution would not be greatly pertubated.
{Xt} is a multivariate Gaussian process in dependent with density fθ (.) . We estimate the parameters in the general multivariate linear processes in (1).
In this paper is to prove a general estimation of the parameter vector θ by the minimum Hellinger distance Method (MHD). The only existing examples of MHD estimates are related to i.i.d. sequences of random variables’s [2-4]. For long memory univariate linear processes see Bitty and Hili [5]. The long memory concept appeared since 1950 from the works of Hurst in hydraulics. The process 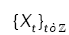 is said to be a long memory process if in (1), λ is a parameter of long memory, and 1 / 2 <λij < 1 for j = 1;…;d and i = 1;…;d.
is said to be a long memory process if in (1), λ is a parameter of long memory, and 1 / 2 <λij < 1 for j = 1;…;d and i = 1;…;d.
The paper developers in section 2, some assumptions and lemmas, essentially based on the work of Tae-Sung Kim, Mi-Hwa Ko and Sung-Mo Chung [1] and the work of Theophilos Cacoullos [6]. Our main results arein section 3, based on work of Bitty and Hili [5] which show consistency and the asymptotic properties of the MHD estimators of the parameter θ. We conclude with some examples,
Parzen [7] gave the asymptotic properties of a class of estimates fn(x) an univariate density function f(x) on the basis of random sample X1,…,Xn from f(x). Motivated as in Parzen, we consider estimates fn(x) ofthe density function f(x) of the following form:
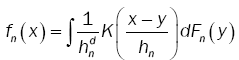 (6)
(6)
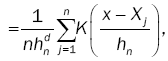 (7)
(7)
where Fn(x) denotes the empirical distribution function based on the sample of n independent observations X1,…, Xn on the random d-dimensional vector X with chosen to satisfy suitable conditions and {hn} is a sequence of positive constants which in the sequel will always satisfy hn→ 0, as n→8 .We suppose K(y) is a bore scalar function on Ed such that
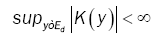 (8)
(8)
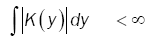 (9)
(9)
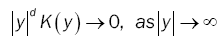 (10)
(10)
where y denotes the length of the vector.
And
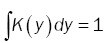 (11)
(11)
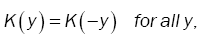 (12)
(12)
also K(y) is absolutely integrable (hence f(x) is uniformly continuous).
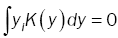 (13)
(13)
and 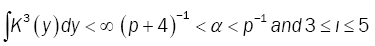 (14)
(14)
See Theopilos Cacoullos [6] and Bitty, Hili [5]
Notations and Assumptions: Let 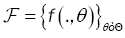 be a family of functions whereT is a compact parameter set
be a family of functions whereT is a compact parameter set 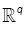 of such that for all θ ε Θ , f(.,θ ) :
of such that for all θ ε Θ , f(.,θ ) : 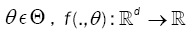 is a positive integral function. Assume that f(.,θ) satisfies the following assumptions.
is a positive integral function. Assume that f(.,θ) satisfies the following assumptions.
(A2): For all θ ,µ ε Θ,θ ≠ µ is a continuous differentiable function at θ εΘ .
(A2): (i) 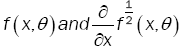 have a zero Lebesgue measure and f (.,θ)is bounded on
have a zero Lebesgue measure and f (.,θ)is bounded on 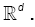
(ii) For θ ,µ ò Θ,θ ≠ µ implies that 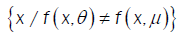 is a set of positive Lebesgue mesure, for all xò
is a set of positive Lebesgue mesure, for all xò 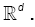
(A3): K the kernel function such that
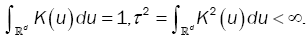
(A4): The bandwidths {bn} satisfy natural conditions, 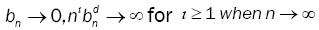 for ι ≥ = 1 when n→∞
for ι ≥ = 1 when n→∞
(A5): There exists a constant ß>0 such that 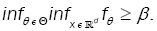
Let F denote the set of densities with respect to the Lebesgue measure on 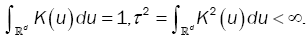 Define the functional
Define the functional 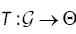 in the following: Let
in the following: Let 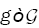 .Denote by B(g) the set
.Denote by B(g) the set 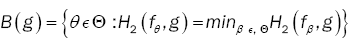 where H2 is the Hellinger distance.
where H2 is the Hellinger distance.
If B(g) is reduced to a unique element, then define T(g) as the value of this element. Elsewhere, we choose an arbitrary but unique element of these minimums and call it T(g).
Lemma 1: Let 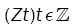 be a strictly stationary associated sequence of d–dimensional random vectors with E(Zt) = 0, E(Zt) < +8 and positive definite covariance matrix ÃÂó as (5). Let (Xt) be a d-variate linear process defined as in (1). Assume that
be a strictly stationary associated sequence of d–dimensional random vectors with E(Zt) = 0, E(Zt) < +8 and positive definite covariance matrix ÃÂó as (5). Let (Xt) be a d-variate linear process defined as in (1). Assume that
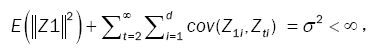 (15)
(15)
then, the linear process(Xt) fulfills the limit central theorem, that is, 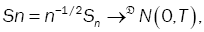 (16)
(16)
Where →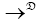 denotes the convergence in distribution and N (0, T) indicates an normal distribution with mean zero vector and covariance matrix T defined in (4).
denotes the convergence in distribution and N (0, T) indicates an normal distribution with mean zero vector and covariance matrix T defined in (4).
For the proof of lemma 1, see theorem 1.1 of Tae-Sung Kim, Mi-Hwa Ko and Sung-Mo Chung [1]
Lemma 2: To remark 3.2 and theorem 3.5 of Tae-Sung Kim, Mi-Hwa Ko and Sung-Mo Chung [1], we have
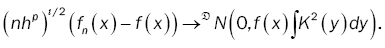 (17)
(17)
For the proof of lemma 2, see Tae-Sung Kim, Mi-Hwa Ko and Sung-Mo Chung [1]
Lemma 3: Assume that (A5) holds. If f1 is continuous on 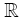 and if for almost all x, h is continuous on Φ , then
and if for almost all x, h is continuous on Φ , then
(i) for all 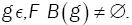
(ii) If B(g) is reduced to an unique element, then t is continuous on g Hellinger topology.
(iii) T (fθ ) =θ Uniquely on Θ
Proof: See Lemma 3.1 in Bitty and Hili [5].
Lemma 4: Assume that 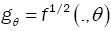 satisfies assumptions (A1),-(A3). Then, for all sequence of density
satisfies assumptions (A1),-(A3). Then, for all sequence of density 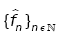 converges to fθ in the Hellinger topology.
converges to fθ in the Hellinger topology.
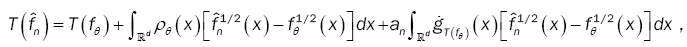
where,
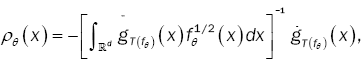
With an a(q×q) - matrix whose components tends to zero n→∞
Proof: See Theorem 2 in Beran [2]
Lemma 5: Under assumptions (A3), if the bandwidth bn is an theorems 1 and 2, if f(.,θ) is continuous with a compact support. And if the density f(.,θ) of the observations satisfies assumptions(A1)-(A2). Then 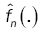 converges to f(.,θ) in the Hellinger topology.
converges to f(.,θ) in the Hellinger topology.
Proof of lemma 8
Under assumption (A2), (A3) and (A5) and lemma 2, we have
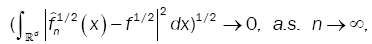
Then 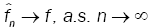 in Hellinger topology
in Hellinger topology
This method has been introduced by Beran [2] for independent samples, developed by Bitty and Hili [5] for linear univariate processes dependent in long memory. The present paper suppose the process independent multivariate with associated random vectors under same condition of Bittyand Hili [5] in long memory. The minimum Hellinger distance estimate of the parameter vector is obtained via a nonparametric estimate of the density of the process (Xt). We define 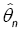 as the value of θ ε Θ which minimizes the Hellinger distance
as the value of θ ε Θ which minimizes the Hellinger distance 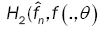
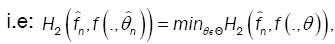
where 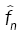 is the nonparametric estimate of f(.,θ) and
is the nonparametric estimate of f(.,θ) and
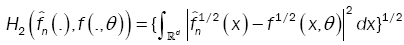
There exist many methods of non parametric estimation in the literature. See for instance Rosenblatt [8] and therein. For computational reasons, we consider the kernel density estimate which is defined in section 2. Before analyzing the optimal properties of 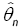 we need some assumptions.
we need some assumptions.
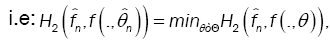
where 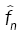 is the nonparametric estimate of f(.,θ) and
is the nonparametric estimate of f(.,θ) and
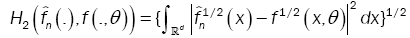
Asymptotic properties
Theorem 1 (Almost Sure Consistency): Assume that (A1)-(A5) hold. Then, 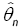 almost surely converges toθ.
almost surely converges toθ.
For the proof, see section 3.
Let denote by Jn as: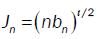
Let us denote by 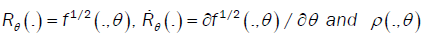 the following function.
the following function.
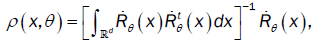
Where 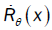 is a quantity which exists, and t denotes the transpose.
is a quantity which exists, and t denotes the transpose.
Condition 1:
We have the (q × q) matrix sequence vn in lemma 4 and the sequence Jn are such that Jnvn tend to zero as  .
.
Theorem 2 (Asymptotic distribution): Assume that (A1)-(A6) and condition 1 hold. If
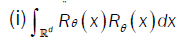 is a nonsingular (qq) -matrix,
is a nonsingular (qq) -matrix,
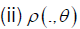 admits a compact support then, we have
admits a compact support then, we have 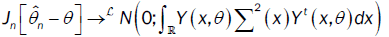
For the proof, see section 3.
Appendices
Proof of theorem 1
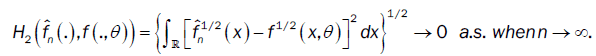
From lemma 3,
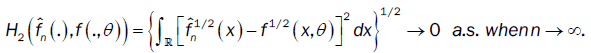
As 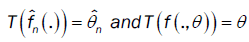 uniquely, the remainder of proof follows from the continuity of the functional T(.) in lemma 1.
uniquely, the remainder of proof follows from the continuity of the functional T(.) in lemma 1.
Proof of theorem 2
From lemma 2 and the proof of theorem 2 of Bitty and Hili [5], we have
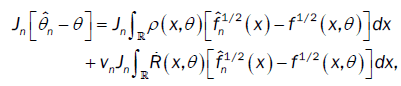
where an a (d×d)-matrix whose components tend to zero in probability when n→ 8 .
Under condition 1, we have
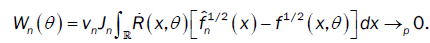
So the limiting distribution of 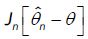 depends on the limiting distribution of
depends on the limiting distribution of 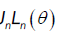 , With
, With
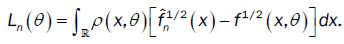
For a = 0 , b = 0, we have the algebraic identity
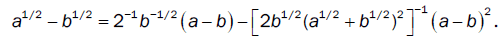
For 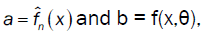 we have
we have
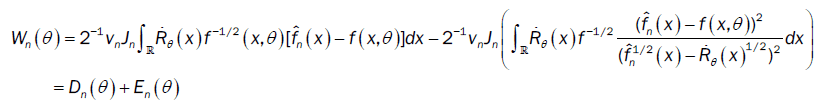
With
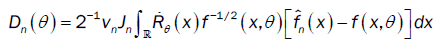
And
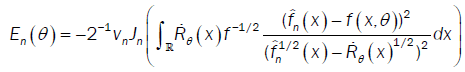
From assumption (A6), then 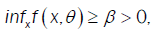
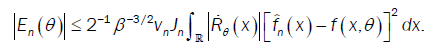
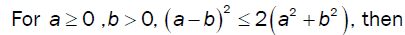
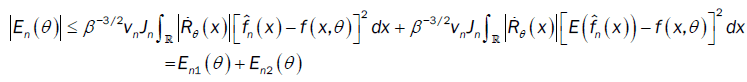
With
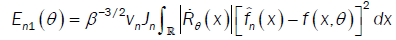
And
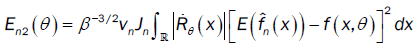
Under assumptions (A1)-(A2) we apply Taylor Lagrange in order 2 and assumption (A4) we have:
So
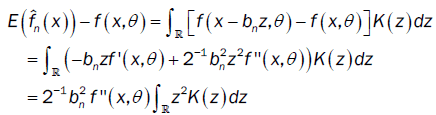
So
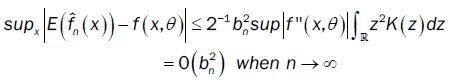
Furthermore, we have 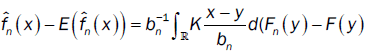
where Fn(.) and F(.) are respectively the empirical distribution function and distribution function of the process. By integration by part, we have
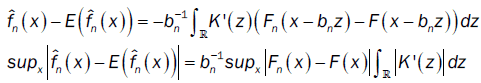
From Ho and Hsing [9,10] (theorem 2.1 and remark 2.2) and assumptions (A2) and (A4), we have
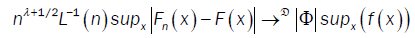
where Φ is a standard Gaussian random variable and !D denotes convergence in distribution.
So
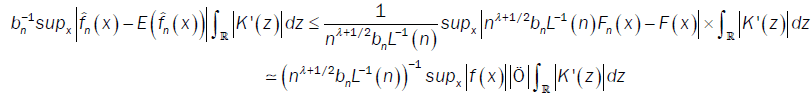
where 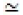 denotes the equivalence in distribution affinity. For all ξ >0,
denotes the equivalence in distribution affinity. For all ξ >0,
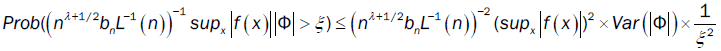
The convergence of 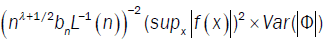 depends on the convergence of
depends on the convergence of 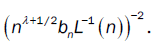
So under assumptions  we have
we have
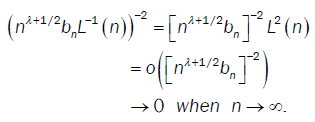
We have 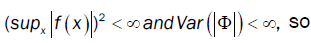
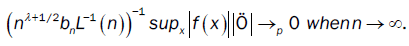
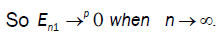
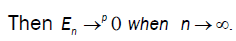
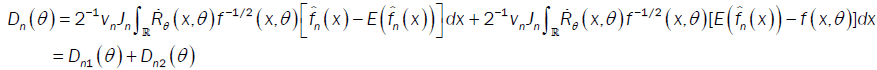
With
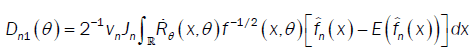
and
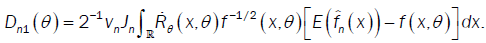
Under assumptions (A1) - (A2) we apply Taylor-Lagrange formula in 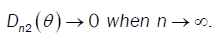 order 2 and assumption (A4), we have
order 2 and assumption (A4), we have
Furthermore, from propositions 1, 2 and 3, we have
Part (a)
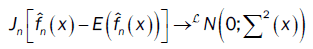
or
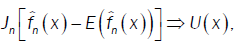
Where 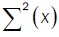 and U(x) take values according to the different points of the proof of lemma 3:
and U(x) take values according to the different points of the proof of lemma 3:
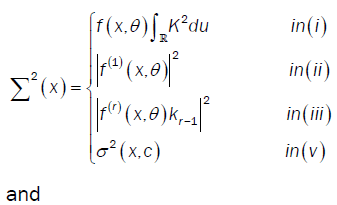
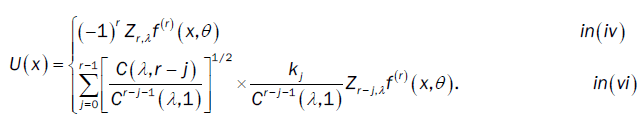
Here 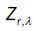 is the Multiple Wiener-Itô Integral defined in the relation (9) of section 1.1 and σ2 (x,c) is defined in the first point of proposition 3. Denote by
is the Multiple Wiener-Itô Integral defined in the relation (9) of section 1.1 and σ2 (x,c) is defined in the first point of proposition 3. Denote by 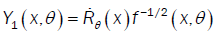
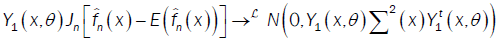
or
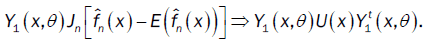
We deduce that
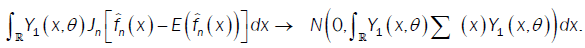
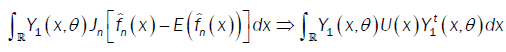
Were call that  then
then 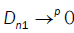 So we conclude that D → 0 when n→∞
So we conclude that D → 0 when n→∞
Part (b)
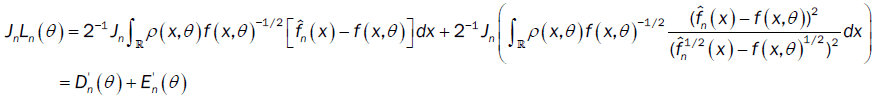
with
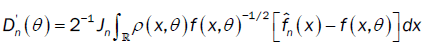
and
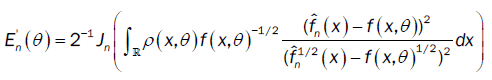
From part (a), the proof of 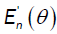 is the same as the proof of
is the same as the proof of 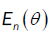 . Were place
. Were place 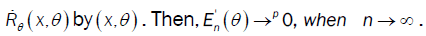
Hence it suffices to prove that the limiting distribution of 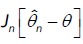 is the same as the limiting distribution of
is the same as the limiting distribution of 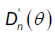 .Since
.Since
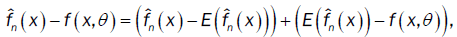
then
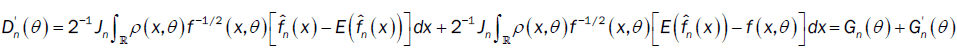
with
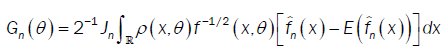
and
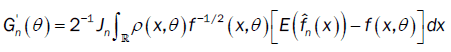
From the proof of lemma 3 (part (b)), we have:
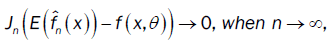
then
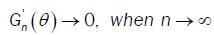
From propositions 1, 2 and 3, we have:
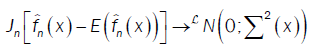
or
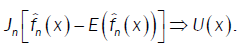
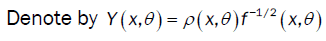
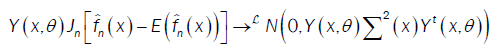
or
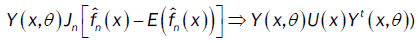
We deduce that
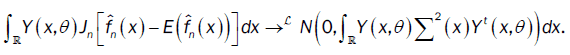
or
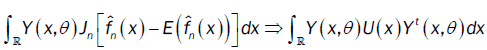
So,
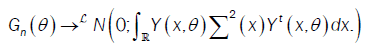
or
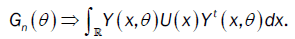
Then,
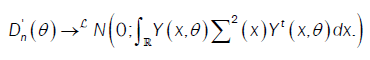
or
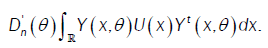
We conclude that we have either an asymptotic normal distribution or an asymptotic process towards the Multiple Wiener- Itô Integral.