Keywords
|
| Face recognition, Normalization, DoG, LBP, LTP, K-means |
INTRODUCTION
|
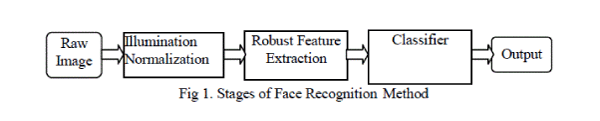
| This paper focuses mainly on the issue of robustness to illumination variations. For example, a face verification system for a portable device should be able to verify a client at any time (day or night) and in any place (indoors or outdoors). Unfortunately, facial appearance depends strongly on the ambient lighting Traditional approaches for dealing with this issue can be broadly classified into three categories: appearance-based, normalization-based, and feature-based methods[1][2]. In this paper, we propose an integrative framework that combines the strengths of all three of the above approaches. The overall process can be viewed as a pipeline consisting of image normalization, feature extraction, and Classifier, as shown in Fig. 1. Each stage increases resistance to illumination variations and makes the information needed for recognition more manifest. The method centres on a rich set of robust visual features that is selected to capture as much as possible of the available information. A well-designed image pre-processing pipeline is prepended to further enhance robustness. In this paper, combinations of all the above approaches are used. The schematic representation of the whole framework is given as follows, which contains pre-processing stage, feature extraction stage and Classifier stage for recognition. |
 |
 |
| Gamma correction – An initial level of corrections are made for illumination deficiency. However this does not remove the influence of overall intensity gradients such as shading effects Difference of Gaussians (DoG) Filtering – This involves the subtraction of one blurred version of an original gray scale image from another less blurred version of the original. |
| This enhances the fine details of the image. |
| Masking – At this stage, irrelevant regions like of the images are masked out. |
| Contrast Equalization– At this stage, intensities of the image are rescaled. This step is required to standardize the intensity values for further processing. |
LOCAL TEXTURE EXTRACTION
|
A. LOCAL BINARY PATTERNS (LBP)
|
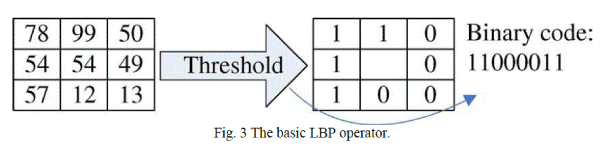
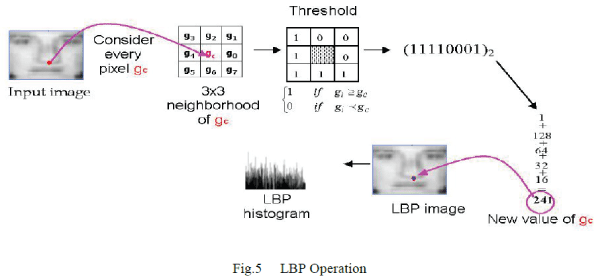
| The LBP operator [3] is one of the best performing texture descriptors and it has been widely used in various applications. It has proven to be highly discriminative and its key advantages, namely its invariance to monotonic gray level changes and computational efficiency, make it suitable for demanding image analysis tasks .The idea of using LBP for face description is motivated by the fact that faces can be seen as a composition of micro-patterns which are well described by such operator .The LBP operator was originally designed for texture description. The operator assigns a label to every pixel of an image by thresholding the 3x3-neighborhood of each pixel with the centre pixel value and considering the result as a binary number. Then the histogram of the labels can be used as a texture descriptor. See Fig 3 for an illustration of the basic LBP operator. Formally, the LBP operator takes the form |
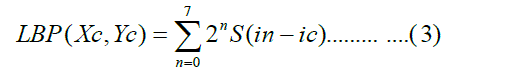 |
| where in this case n runs over the 8 neighbours of the central pixel c ,ic and in are gray level values at c and n s(u)=1 if u ≥ 0 and 0 otherwise |
 |
| Two extensions of the original operator were made in [3]. The first defined LBPs for neighbourhoods of different sizes, thus making it feasible to deal with textures at different scales. The second defined the so-called uniform patterns:A local binary pattern is called uniform if the binary pattern contains at most two bitwise transitions from 0 to 1 or vice versa when the bit pattern is considered circular. For example,the patterns 00000000 (0 transitions), 01110000 (2 transitions) and 11001111 (2 transitions) are uniform whereas the patterns 11001001 (4 transitions) and 01010011 (6 transitions) are not. In the computation of the LBP histogram, uniform patterns are used so that the histogram has a separate bin for every uniform pattern and all non-uniform patterns are assigned to a single bin. Uniformity is important because it characterizes the patches that contain primitive structural information such as edges and corners. Ojala et al. observed that although only 58 of the 256 8-bit patterns are uniform, nearly 90% of all observed image neighbourhoods are uniform and many of the remaining ones contain essentially noise. Thus, when histogramming LBPs the number of bins can be reduced significantly by assigning all non uniform patterns to a single bin, typically without losing too much information. |
| The facial image is divided into local regions and texture descriptors are extracted from each region independently. The descriptors are then concatenated to form a global description of the face. See Fig 4 for an example of a facial image divided into rectangular regions. |
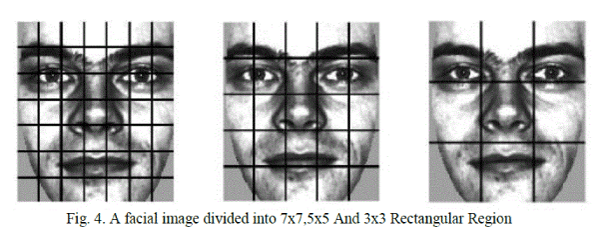 |
| The basic histogram can be extended into a spatially enhanced histogram which encodes both the appearance and the spatial relations of facial regions. As the m facial regions R0,R1….Rm-1 have been determined, a histogram is computed independently within each of the m regions. The resulting m histograms are combined yielding the spatially enhanced histogram. The spatially enhanced histogram has size mxn where n is the length of a single LBP histogram. In the spatially enhanced histogram, we effectively have a description of the face on three different levels of locality: the LBP labels for the histogram contain information about the patterns on a pixel-level, the labels are summed over a small region to produce information on a regional level and the regional histograms are concatenated to build a global description of the face. It should be noted that when using the histogram-based methods, despite the examples in Fig 4, the regions R0,R1…..Rm-1, do not need to be rectangular. Neither do they need to be of the same size or shape, and they do not necessarily have to cover the whole image. For example, they could be circular regions located at the fiducial points like in the EBGM method. It is also possible to have partially overlapping regions. |
 |
B. LOCAL TERNARY PATTERNS (LTP)
|
| LBPs have proven to be highly discriminative features for texture classification [3] and they are resistant to lighting effects in the sense that they are invariant to monotonic gray-level transformations. However because they threshold at exactly the value of the central pixel they tend to be sensitive to noise, particularly in near-uniform image regions, and to smooth weak illumination gradients. Many facial regions are relatively uniform and it is legitimate to investigate whether the robustness of the features can be improved in these regions. This section extends LBP to 3-valued codes, LTP, in which gray-levels in a zone of width around ic are quantized to zero, ones above this are quantized to +1 and ones below it to -1, i.e., the indicator S(u) is replaced with a 3-valued function |
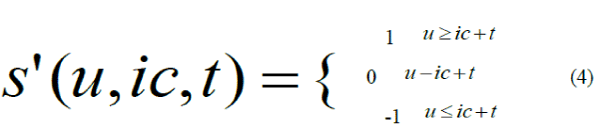 |
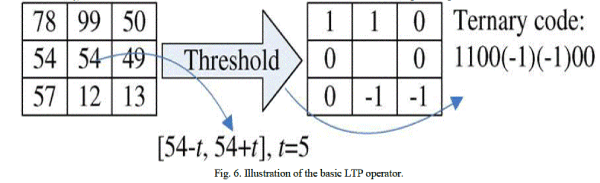
| and the binary LBP code is replaced by a ternary LTP code. Here t is a user-specified threshold—so LTP codes are more resistant to noise, but no longer strictly invariant to gray-level transformations. The LTP encoding procedure is illustrated in Fig. 6. Here the threshold was set to 5, so the tolerance interval is [49, 59]. |
 |
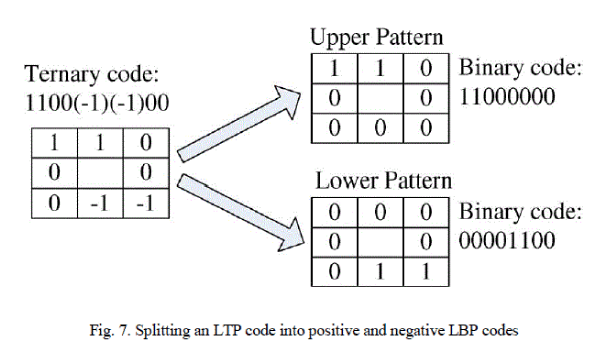
| When using LTP for visual matching, we could use valued codes, but the uniform pattern argument also applies in the ternary case. For simplicity, the experiments below use a coding scheme that splits each ternary pattern into its positive and negative halves as illustrated in Fig. 7, subsequently treating these as two separate channels of LBP descriptors for which separate histograms and similarity metrics are computed, combining the results only at the end of the computation. |
 |
C. DISTANCE TRANSFORM BASED SIMILARITY MEASURE
|
| The used similarity metric is an LBP based method for face recognition [2] that divides the face into a regular grid of cells and histograms the uniform LBP’s within each cell, finally using nearest neighbor classification in the χ2 histogram distance for recognition: |
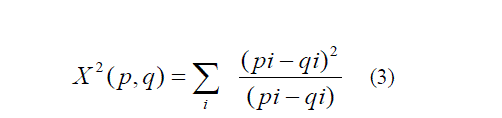 |
| Here p,q are image region descriptors (histogram vectors), respectively |
| However, subdividing the face into a regular grid seems somewhat arbitrary: the cells are not necessarily well aligned with facial features, and the partitioning is likely to cause both aliasing (due to abrupt spatial quantization of descriptor contributions) and loss of spatial resolution (as position within each grid cell is not coded). Given that the overall goal of coding is to provide illumination- and outlier-robust visual correspondence with some leeway for small spatial deviations due to misalignment, it seems more appropriate to use a Hausdorff- distance-like similarity metric that takes each LBP or LTP pixel code in image and tests whether a similar code appears at a nearby position in image , with a weighting that decreases smoothly with image distance. Such a scheme should be able to achieve discriminant appearance-based image matching with a well-controllable degree of spatial looseness. We can achieve this using distance transforms. Given a 2-D reference image, we find its image of LBP or LTP codes and transform this into a set of sparse binary images , one for each possible LBP or LTP code value (i.e., 59 images for uniform codes). Each specifies the pixel positions at which its particular LBP or LTP code value appears. We then calculate the distance transform image of each . Each pixel of gives the distance to the nearest image pixel with code (2-D Euclidean distance is used in the experiments below). The distance or similarity metric from image to image is then |
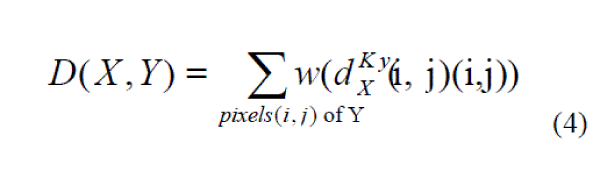 |
| Here, is the code value of pixel of image and is a user-defined function4 giving the penalty to include for a pixel at the given spatial distance from the nearest matching code in . In our experiments we tested both Gaussian similarity metrics and truncated linear distances. Their performance is similar, with truncated distances giving slightly better results overall. For 120x120 face images in which an iris or nostril has a radius of about six pixels and overall global face alignment is within a few pixels, our default parameter values were pixels and pixel. |
D. K-MEAN ALGORITHM
|
| K-means is one of the simplest unsupervised learning algorithms that solve the well known clustering problem. The procedure follows a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters) fixed a priori. The main idea is to define k centroids, one for each cluster. These centroids should be placed in a cunning way because of different location causes different result. So, the better choice is to place them as much as possible far away from each other. The next step is to take each point belonging to a given data set and associate it to the nearest centroid. When no point is pending, the first step is completed and an early group age is done. At this point we need to re-calculate k new centroids as bary centers of the clusters resulting from the previous step. After we have these k new centroids, a new binding has to be done between the same data set points and the nearest new centroid. A loop has been generated. As a result of this loop we may notice that the k centroids change their location step by step until no more changes are done. In other words centroids do not move any more Finally, this algorithm aims at minimizing an objective function, in this case a squared error function. The objective function,Where is a chosen distance measure between a data point and the cluster centre , is an indicator of the distance of the n data points from their respective cluster centers. |
| Our implementation Steps: |
| 1. The distance between testing template with the database is calculated. |
| 2. All the distances are sorted in ascending order |
| 3. First 5 values are used to as K-Mean centroid |
| 4. The repetitive value using mode is found to indentify the class |
EXPERIMENTAL RESULTS
|
| Following are the results after the preprocessing stage: |
 |
 |
| Final results after distance transform matching algorithm and K-means algorithm |
 |
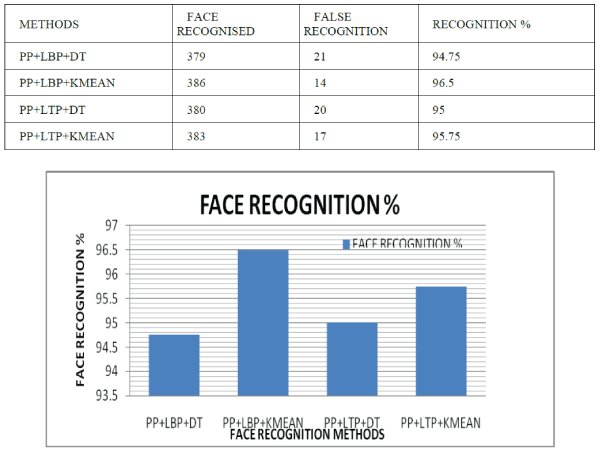
| We have used the cropped yale database by using it we got recognition rate as follow |
 |
CONCLUSION
|
| We have presented new methods for face recognition under uncontrolled lighting based on robust preprocessing and an extension of the LBP local texture descriptor. The main contributions are as follows:a simple, efficient image preprocessing chain whose practical recognition performance is comparable to or better than current (often much more complex) illumination normalization methods, a rich descriptor for local texture called LTP that generalizes LBP while fragmenting less under noise in uniform regions: a distance transform based similarity metric that captures the local structure and geometric variations of LBP/LTP face images better than the simple grids of histograms that are currently used, Recognition rate is further improved by using kmean classifier |
References
|
- R Y. Adini, Y. Moses, and S. Ullman, “Face recognition: The problem of compensating for changes in illumination direction,” IEEE Trans. Pattern Analysis & Machine Intelligence, vol. 19, no. 7, pp. 721–732, 1997.
- T. Ahonen, A. Hadid, and M. Pietikainen, “Face description with local binary patterns: Application to face recognition,” IEEE Trans. Pattern Anal. Mach Intell., vol. 28, no. 12, pp. 2037–2041, Dec. 2006.
- T. Ojala, M. Pietikainen, and T. Maenpaa, “Multiresolution gray-scale and rotation invarianat texture classification with local binary patterns,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 24, no. 7, pp. 971–987,Jul. 2002.
- X. Tan and B. Triggs, “Enhanced local texture feature sets for face recognition under difficult lighting conditions,” in . IEEE Trans. Image processing., vol. 19, no. 6, pp. 1635–1650, june. 2010.
|