Factorial Optimization of Gypsum Addition to Foundry Slag during Production of Maximum-Compressive-Strength Compliant Cement

Abstract

This paper presents the predictability and optimization of gypsum addition to foundry slag during production of maximum-compressive-strength compliant cement using a empirically derived model. The model expressed as; β = 0.04 α – 0.0024 α2 – 0.0288 is quadratic in nature, indicating that the slag cement maximum-compressive-strength is dependent on the optimum concentration of gypsum added. The slag cement compressive strengths per unit gypsum addition are 0.0160 and 0.0208 N mm-2/% as obtained from experiment and derived model respectively. The correlations between compressive strength and concentration of gypsum addition are 0.8839 and 0.9977 as obtained from experiment and derived model respectively. The maximum deviation of the model-predicted slag cement compressive strength from the corresponding experimental value is less than 12%. The validity of the model was rooted on the expression 17.3611 β + 0.0417 α2 = 0.6944 α – 0.5 where both sides of the expression are correspondingly approximately equal. The optimum concentration of gypsum addition which inputs maximum-compressive-strength: 0.1378 N/mm2 to the slag cement is 8.3333 %. At 15% gypsum addition, the slag cement compressive strength is minimum. Beyond 15% gypsum addition, the slag cement compressive strength becomes only imaginary in compression; a situation that typifies a build-up in its tensile strength.

Keywords

Prediction, Optimization, Gypsum Addition, Slag cement

Introduction

Cement plays a very important role in the building and construction sector and so there is need to support researches aimed at improving the quality of cement produced through incorporation of industrial wastes and cheaper locally acquired material. There is also need to try out different materials to produce materials of similar characteristics to cement.

Materials added to form cement are expected to have the necessary performance characteristics to satisfy the specifications determined by its application [1]. In addition, it should be inoffensive concerning health and the environment. Finally, the incorporation of the waste should not impair concrete durability. Traditional assessment methods must therefore be adopted to evaluate these new materials [2]. The ash is considered as experimental waste because of, in particular, its high content of soluble salt (Sugar) [3]. The durability and the environmental impact of concrete are closely connected to its transport properties, which control the kinetics of the penetration of water and aggressive agents into concrete [4]. The movement of chemical species within the material and the leaching of certain chemicals are also closely linked to concrete diffusivity [5].

Research [6] has shown that the essential components of blast furnace slag are the same oxide (such as lime, silica, and aluminum) as are present in Portland cement but differ in proportion. Blast furnace slag is a by-product obtained in the manufacture of pig iron in the blast furnace. It has been put into considerable use in the road and building industries and in the production of cementing materials, as an aggregate in concrete and in the manufacture of slag wool for thermal insulation.

The aim of this work is to develop a model for prediction and optimization of gypsum addition to foundry slag for production of maximum-compressive-strength compliant cement.

Materials And Methods

Materials used and their respective sources and details of the experimental procedure and associated process conditions are as stated in the past report [6].

Model Formulation

Experimental data obtained from research work [6] were used for this work. Computational analysis of the experimental data [6] shown in Table 1, gave rise to Table 2 which indicate that;

Table 1: Variation of compressive strength with the concentration of gypsum added [6]

Tabale 2: Computed parts of model forming equation

Introducing the values of N, S, K and Ne into equation (1) reduces it to;

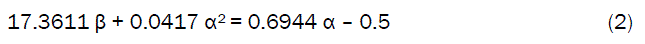
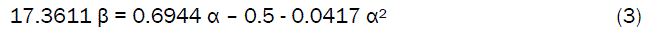
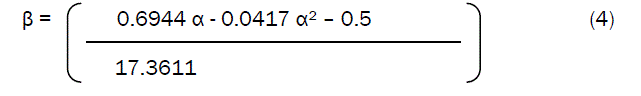
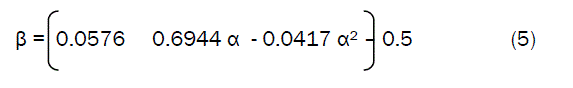
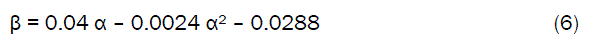
Where

(β) = Compressive strength (N/mm2)

N = 17.3611; Compressive coefficient of the cement (determined using C-NIKBRAN [7]

(α) = Concentration of gypsum added (%)

S = 0.0417; Gasification constant during gypsum-slag mixing (determined using C- NIKBRAN [7])

K = 0.6944; Gypsum-slag interaction factor (determined using C-NIKBRAN [7])

Ne= 0.5; Slag grade (determined using C-NIKBRAN [7])

Boundary and Initial Condition

Consider foundry slag paste of required consistency (in a cylindrical container) interacting with quantities of gypsum. The container’s atmosphere was not contaminated i.e (free of unwanted gases, dusts and other micro organisms). Range of gypsum addition: 3-5 %. Resultant range of compressive strength obtained (based added gypsum): 0.073- 0.105 (N/mm2). Mass of wastes used, resident time, treatment temperature, and other process conditions are as stated in the experimental technique [6].

The boundary conditions are: free movement of oxygen across the cylindrical container. At the bottom of the particles, a zero gradient for the gas scalar are assumed and also for the gas phase at the top of the slag paste. The treated slag paste is stationary. The sides of the waste particles are taken to be symmetries.

Results And Discussion

The derived model is equation (6). The computational analysis of Table 1 gave rise to Table 2

Model Validation

The validity of the model is strongly rooted on equation (2) where both sides of the equation are correspondingly approximately equal. Table 3 also agrees with equation (2) following the values of 17.3611 β + 0.0417 α² and 0.6944 α – 0.5 evaluated from the experimental results in Table 1. Furthermore, the derived model was validated by comparing the compressive strength (of the slag cement) predicted by the model and that obtained from the experiment [6]. This was done using the 4th Degree Model Validity Test Techniques (4th DMVTT); computational, graphical, statistical and deviational analysis [8].

Table 3: Variation of 17.3611 β + 0.0417 α² with 0.6944 α – 0.5

Computational Analysis

A comparative analysis of the results computed from experimental and model-predicted compressive strength was carried to ascertain the degree of validity of the derived model. This was done by comparing compressive strength per unit gypsum addition obtained by calculations involving experimental results, and modelpredicted results obtained directly from the model.

Compressive strength of slag cement per unit gypsum addition βg (N mm-2/%) was calculated from the equation;

Therefore, a plot of compressive strength against concentration of gypsum addition as in Fig. 1 using experimental results in Table 1, gives a slope, S at points (3, 0.073) and (5, 0.105) following their substitution into the mathematical expression;

Figure 1: Coefficient of determination between compressive strength and concentration of gypsum added as obtained from the experiment [6].

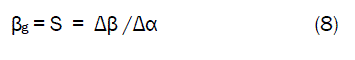
Equation (8) is detailed as

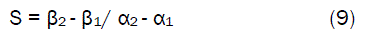
Where

Δβ = Change in the compressive strength β2, β1 at two gypsum concentrations α², α 1. Considering the points (3, 0.073) and (5, 0.105) for (α1, β1) and (α², β 2) respectively, and substituting them into equation (9), gives the slope as 0.0160 N mm-2 /% which is the slag cement compressive strength per unit gypsum addition during the actual experimental process. Also similar plot (as in Fig. 2) using model-predicted results gives a slope. Considering points (3, 0.0696) and (5, 0.1112) for (α1, β1) and (α², β2) respectively and substituting them into equation (9) gives the value of slope, S as 0.0208 N mm-2 /%. This is the model-predicted slag cement compressive strength per unit gypsum addition. A comparison of these two values of the slag compressive strength unit gypsum addition shows proximate agreement.

Figure 2: Coefficient of determination between compressive strength and concentration of gypsum added as predicted by model

Graphical Analysis

Comparison of slag cement compressive strength per unit gypsum addition as obtained from experiment [6] and derived model the purpose of validity testing is achieved by considering the R2 values (coefficient of determination). The values of the correlation coefficient, R calculated from the equation;

using the r-squared values (coefficient of determination) from Figs. 1 and 2 show better correlation; 0.9977 for the derived model than for the experiment [6]; 0.8839 respectively between compressive strength and concentration of gypsum added. This is a clear indication that the model predicts accurate and reliable slag cement compressive strength which are in proximate agreement with values from actual the experiment [6], hence confirming the validity of the derived model.

Comparative graphical analysis of Fig. 3 shows very close alignment of the curves from the experimental (ExD) and model-predicted (MoD) slag cement compressive strength per unit gypsum addition respectively. Furthermore, the degree of alignment of these curves is indicative of the proximate agreement between both experimental and model-predicted compressive strength.

Figure 3: Comparison of the compressive strength per unit concentration of gypsum as obtained from experiment [6] and derived model.

Deviational Analysis

Critical comparative analysis of compressive strength from experiment [6] and derived model revealed insignificant deviations on the part of the model-predicted values relative to values obtained from the experiment. This is attributed to the fact that the surface properties of the slag material and the physiochemical interactions between the slag material and added gypsum (under the influence of the treatment temperature) which were found to have played vital roles during the process [6] were not considered during the model formulation. This necessitated the introduction of correction factor, to bring the model-predicted compressive strength to those of the corresponding experimental values.

Deviation (Dv) of model-predicted compressive strength from that of the experiment [6] is given by

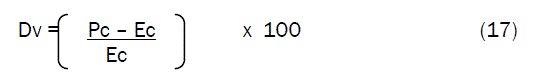
Correction factor (Cr ) is the negative of the deviation i.e

Therefore

Where

Pc = Model-predicted compressive strength (N/mm2)

Ec = Compressive strength obtained from experiment (N/mm2)

Cr = Correction factor (%)

Dv = Deviation (%)

Introduction of the corresponding values of Cr from equation (19) into the model gives exactly the corresponding experimental compressive strength.

Comparative analysis of Figs. 4 and 5 shows that the maximum deviation of the model-predicted slag compressive strength from the corresponding experimental values is less than 12% and quite within the acceptable deviation limit of experimental results.

Figure 4: Variation of model-predicted compressive strength with its associated deviation from experimental values

Figure 5: Variation of deviation (of model-predicted compressive strength) concentration of added gypsum

These figures show that least and highest magnitudes of deviation of the model-predicted compressive strength (from the corresponding experimental values) are - 2.29 and -11.62 % which corresponds to compressive strengths: 0.1026 and 0.0928 N/mm2 as well as concentration of gypsum addition: 4.5 and 4 % respectively.

Analysis of Figs. 4-7 indicates that the orientation of the curve in Figs. 6 and 7 is opposite those of the deviation of model-predicted compressive strength in Figs. 4 and 5. This is because correction factor is the negative of the deviation as shown in equations (18) and (19). It is believed that the correction factor takes care of the effects of the surface properties of the slag material and the physiochemical interaction between the slag material and the added gypsum which (affected experimental results) were not considered during the model formulation. Figs. 6 and 7 indicate that the least and highest magnitudes of correction factor to the model-predicted compressive strength are +2.29 and +11.62 % which corresponds to compressive strengths: 0.1026 and 0.0928 N/mm2 as well as concentration of gypsum addition: 4.5 and 4 % respectively.

Figure 6: Variation of correction factor (to model-predicted values) with compressive strength

Figure 7: Variation of correction factor (to model-predicted compressive strength) with concentration of gypsum addition.

Optimization of gypsum addition

Compressive strength predicted by the derived model (equation (6)); β = 0.04 α – 0.0024 α² – 0.0288 is based on the concentration of gypsum addition. Optimization of gypsum addition was achieved by differentiating the derived models (equations (6)) with respect to α (and equating to zero) in order to determine the value of α at which β is maximum.

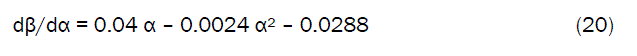
Differentiation of equations (20) with respect to α reduces them respectively to;

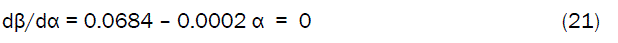
The value of α = 8.3333 %, evaluated from equations (22) is the optimum concentration of gypsum addition which invariably gives the maximum compressive strength, β as 0.1378 N/mm2 on substituting the value of α = 8.3333 % into the derived model in equation (6).

Confirmation of the maximum and optimum values of β and α respectively was carried out by substituting an assumed range of values of the concentration of gypsum addition α = 10, 12, 14, 15, 16, 17 and 20 %.

Critical analysis of Fig. 8 indicates that the minimum compressive strength of the slag cement (0.0312 N/mm2) could be obtained at 15 % gypsum addition and beyond that concentration, the resultant compressive strength of the slag cement becomes only imaginary in compression (having negative values). It is therefore suspected that beyond this point (15% gypsum addition) the tensile strength of the slag cement begins to build-up.

Figure 8: Predicted maximum compressive strength of the slag cement at predicted optimum concentration of gypsum addition.

Conclusion

The model predicts and optimizes gypsum addition to foundry slag in order to produce maximum-compressive-strength compliant cement. The slag cement compressive strength per unit gypsum addition are 0.0160 and 0.0208 N mm-2/% as obtained from experiment and derived model respectively. The correlations between compressive strength and concentration of gypsum addition are 0.8839 and 0.9977 as obtained from experiment and derived model respectively. The maximum deviation of the model-predicted slag cement compressive strength from the corresponding experimental value is less than 12%. The validity of the model was found to be rooted on the expression 17.3611 β + 0.0417 α² = 0.6944 α – 0.5 where both sides of the expression are correspondingly approximately equal. The optimum concentration of gypsum addition which inputs maximum compressive strength: 0.1378 N/mm2 to the slag cement is 8.3333 %. Beyond 15% gypsum addition, the slag cement compressive strength becomes only imaginary in compression; a situation that gives a build-up in its tensile strength.

References

1. Helmuth R. Fly ash in cement and concrete, Portland Cement Association. J Cement Concrete Res. 1987;30:201-204.
2. Chatterji AK. Adsorption of lime and pozzolanic activity. J Sci Ind Res. (1990). 19B: 493 – 494.
3. Kessler B, Rollet M, Sorrentino F. 1992. Microstructure of cement pastes as incinerators ash host. Proceedings of 1st International Symposium on cement industry solution to waste Management, Calgary. Pp 235 - 251.
4. Pimienta P, Remond S, Rodrigues N and Bournazel JP. 1999. Assessing the Properties of Mortars ontaining Musical Solid Waste Incineration Fly Ash. International Congress, Creating with Concrete, University of Dundee. Pp 319 - 326.
5. Remond S, Pimienta P, and Bentz DP. Effect of the incorporation of municipal solid waste fly ash in cement paste and Mortars. J Cement Concrete Res. 2002;10:12-14
6. Egunlae OO. The Influence of Gypsum on Foundry Slag for Making Cement. IREJEST. 2011;8(1):33-42
7. Nwoye CI. 2008. Data Analytical Memory; C-NIKBRAN
8. Nwoye CI, Onyedika GO, and Ugwuegbu CC. Model Development for the Prediction of Methane Gas Yield during Microbial Treatment of Fruit Wastes. JMME. 2011;6(1):7-16.