International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Fast Fourier Transform Pipeline Architecture for OFDM

Sekhar Babu P1, Dr.Shaik Mastan Vali2
  1. PG Scholar [VLSI], Department of ECE, MVGR College of Engineering, Vizianagaram, AP, India
  2. Professor, Department of ECE, MVGR College of Engineering, Vizianagaram, AP, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Integrated circuits to support digital communication standards are commonly based on a Fast Fourier Transform (FFT) of some length. Flexible length makes the design more usable for configurable algorithm-specific circuits. The proposed project discusses the functional aspects of a FFT design. As the transform length increases the amount of arithmetic involved becomes excessive. This makes Fast Fourier Transform (FFT) to one of today’s most important tools in digital signal processing, as it enables the efficient transformation between time and frequency domain. Over the last decade, researches have been done on how to transmit the data using OFDM transmission over selective channels. The proposed project will show how the FFT is better adapted to the requirements in the application of OFDM at the frequency of 160 MHz. The simulation results show the output of each butterfly by enabling cosimulation of the butterfly outputs using VHDL. The simulation results also show the transmission of data through OFDM technique using FFT implementation. The Synthesizing and implementation (i.e. Translate, Map and Place and Route) of the code is carried out on Xilinx - Project Navigator, ISE 8.2i suite. By this project we have to show the lossless transmission of information.

Keywords
Cognitive Radio, Spectrum Sensing, Efficient Communication, System Security

INTRODUCTION
The main challenging areas in VLSI are performance, speed, cost, and power dissipation [1]. The demand for portable computing devices and communications system are increasing rapidly. These applications require high frequency modules in VLSI circuits. Hence it is important aspect to optimize the frequency during processing. That’s why frequency optimization is one of the main challenges. FFT algorithms are so commonly employed to compute DFTs that the term "FFT" is often used to mean "DFT" in colloquial settings. Formally, there is a clear distinction: "DFT" refers to a mathematical transformation or function, regardless of how it is computed, whereas "FFT" refers to a specific family of algorithms for computing DFTs [2-4].
The OFDM technique is easier to understand and implement, and the sub-channels can be independently adapting in other ways than varying equalization coefficients, such as switching between different QAM constellation patterns and error-correction schemes to match individual sub-channel noise and interference characteristics. Some of the subcarriers in some of the OFDM symbols may carry pilot signals for measurement of the channel conditions. Pilot signals and training symbols may also be used for time synchronization and frequency synchronization. OFDM was initially used for wire, and stationary wireless communications. However with increasing number of applications operating in highly mobile environment, the possibility of using OFDM for such purpose is also investigated. Over the last decade, several researches have been done on how to equalize OFDM transmission over doubly selective channels. The proposed project will show how the FFT is better adapted to the requirements in the application of OFDM at the frequency of 160 MHz’s.
An Application-Specific Integrated Circuit (ASIC) is an integrated circuit (IC) customized for a particular use, rather than intended for general-purpose use [1,5]. For example, a chip designed solely to run a cell phone is an ASIC. Intermediate between ASICs and industry standard integrated circuits, like the 7400 or the 4000 series, are application specific standard products (ASSPs). As feature sizes have shrunk and design tools improved over the years, the maximum complexity (and hence functionality) possible in an ASIC has grown from 5,000 gates to over 100 million.
Modern ASICs often include entire 32-bit processors, memory blocks including ROM, RAM, EEPROM, Flash and other large building blocks. Such an ASIC is often termed a SoC (system-on-a-chip). Designers of digital ASICs use a hardware description language (HDL), such as Verilog or VHDL, to describe the functionality of ASICs. Fieldprogrammable gate arrays (FPGA) are the modern-day technology for building a breadboard or prototype from standard parts; programmable logic blocks and programmable interconnects allow the same FPGA to be used in many different applications. For smaller designs and/or lower production volumes, FPGAs may be more cost effective than an ASIC design even in production.

OFDM AND FFT BASICS
OFDM has developed into a popular scheme for wideband digital communication, whether wireless or over copper wires, used in applications such as digital television and audio broadcasting, wireless networking and broadband internet access.
The primary advantage of OFDM over single-carrier schemes is its ability to cope with severe channel conditions (for example, attenuation of high frequencies in a long copper wire, narrowband interference and frequency-selective fading due to multipath) without complex equalization filters. Channel equalization is simplified because OFDM may be viewed as using many slowly-modulated narrowband signals rather than one rapidly-modulated wideband signal. The low symbol rate makes the use of a guard interval between symbols affordable, making it possible to handle timespreading and eliminate intersymbol interference (ISI). This mechanism also facilitates the design of single frequency networks (SFNs), where several adjacent transmitters send the same signal simultaneously at the same frequency, as the signals from multiple distant transmitters may be combined constructively, rather than interfering as would typically occur in a traditional single-carrier system. In OFDM, the sub-carrier frequencies are chosen so that the sub-carriers are orthogonal to each other, meaning that cross-talk between the sub-channels is eliminated and inter-carrier guard bands are not required. This greatly simplifies the design of both the transmitter and the receiver; unlike conventional FDM, a separate filter for each sub-channel is not required.
The orthogonality requires that the sub-carrier spacing is Hertz, where TU seconds is the useful symbol duration (the receiver side window size), and k is a positive integer, typically equal to 1. Therefore, with N sub-carriers, the total passband bandwidth will be B ≈ N·Δf (Hz). The orthogonality also allows high spectral efficiency, with a total symbol rate near the Nyquist rate for the equivalent baseband signal (i.e. near half the Nyquist rate for the double-side band physical passband signal). Almost the whole available frequency band can be utilized. OFDM generally has a nearly 'white' spectrum, giving it benign electromagnetic interference properties with respect to other co-channel users. OFDM requires very accurate frequency synchronization between the receiver and the transmitter; with frequency deviation the sub-carriers will no longer be orthogonal, causing inter-carrier interference (ICI) (i.e., cross-talk between the subcarriers). Frequency offsets are typically caused by mismatched transmitter and receiver oscillators, or by Doppler shift due to movement. While Doppler shift alone may be compensated for by the receiver, the situation is worsened when combined with multipath, as reflections will appear at various frequency offsets, which is much harder to correct. This effect typically worsens as speed increases, and is an important factor limiting the use of OFDM in high-speed vehicles. Several techniques for ICI suppression are suggested, but they may increase the receiver complexity.
In mathematics, the discrete Fourier transform (DFT) is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function (which is often a function in the time domain) [7-12]. But the DFT requires an input function that is discrete and whose non-zero values have a limited (finite) duration. Such inputs are often created by sampling a continuous function, like a person's voice. Unlike the discrete-time Fourier transform (DTFT), it only evaluates enough frequency components to reconstruct the finite segment that was analyzed. Using the DFT implies that the finite segment that is analyzed is one period of an infinitely extended periodic signal; if this is not actually true, a window function has to be used to reduce the artifacts in the spectrum. For the same reason, the inverse DFT cannot reproduce the entire time domain, unless the input happens to be periodic (forever). Therefore it is often said that the DFT is a transform for Fourier analysis of finite-domain discrete-time functions. The sinusoidal basis functions of the decomposition have the same properties. The input to the DFT is a finite sequence of real or complex numbers making the DFT ideal for processing information stored in computers. In particular, the DFT is widely employed in signal processing and related fields to analyze the frequencies contained in a sampled signal, to solve partial differential equations, and to perform other operations such as convolutions or multiplying large integers. A key enabling factor for these applications is the fact that the DFT can be computed efficiently in practice using a fast Fourier transform (FFT) algorithm. FFT algorithms are so commonly employed to compute DFTs that the term "FFT" is often used to mean "DFT" in colloquial settings. Formally, there is a clear distinction: "DFT" refers to a mathematical transformation or function, regardless of how it is computed, whereas "FFT" refers to a specific family of algorithms for computing DFTs.

IMPLEMENTATION
The orthogonality allows for efficient modulator and demodulator implementation using the FFT algorithm on the receiver side, and inverse FFT on the sender side. Although the principles and some of the benefits have been known since the 1960s, OFDM is popular for wideband communications today by way of low-cost digital signal processing components that can efficiently calculate the FFT.
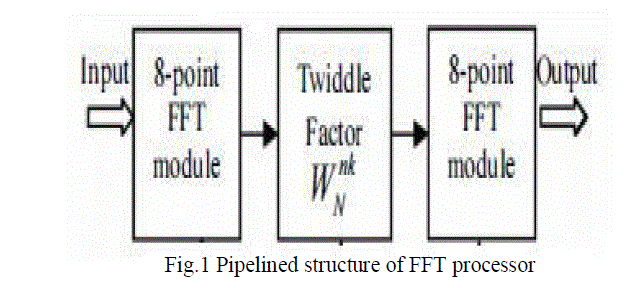image
In a sense, improvements in FIR equalization using FFTs or partial FFTs leads mathematically closer to OFDM, but the OFDM technique is easier to understand and implement, and the sub-channels can be independently adapting in other ways than varying equalization coefficients, such as switching between different QAM constellation patterns and errorcorrection schemes to match individual sub-channel noise and interference characteristics. Some of the sub-carriers in some of the OFDM symbols may carry pilot signals for measurement of the channel conditions Pilot signals and training symbols may also be used for time synchronization and frequency synchronization If differential modulation such as DPSK or DQPSK is applied to each sub-carrier, equalization can be completely omitted, since these noncoherent schemes are insensitive to slowly changing amplitude and phase distortion.OFDM was initially used for wire, and stationary wireless communications. However with increasing number of applications operating in highly mobile environment, the possibility of using OFDM for such purpose is also investigated. Over the last decade, several researches have been done on how to equalize OFDM transmission over doubly selective channels.

RESULTS
Results pertaining to various simulation based experimentation are presented in this section. The chematic diagram of the proposed structure is as shown in the fig.2.
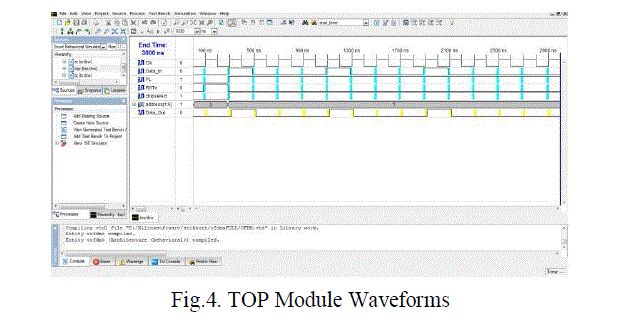
The corresponding RTL schematic diagram is mentioned in the fig.3. The waveforms pertaining to the Top Modeule are specified in the fig.4. The representation of the waveforms of the serial to parallel converter is mentioned in the fig.5. The implementation of the OFDM is represented by applying the BPSK. The BPSK waveforms are represented in the fig.6.
image
image
image
image
image

CONCLUSION
The work demonstrated the implementation of a scalable radix-2 N-point novel FFT processor architecture based on a reasonable balance between performance, power, area, flexibility and scalability parameters was proposed. The results referring to the implementation of the algorithm are mentioned in the fig.2 to fig.6 are used to quote the application part of the project. VHDL language is used to implement synthesis of the scalable FFT processor which was designed and simulated using ModelSim and synthesized on an Altera Stratix V FPGA device 5SGSMD5K2F40C2. The proposed architecture outperforms the existing fixed and variable length FFT processors in terms of speed, power, area, flexibility and scalability. In addition, the processor architecture can also be adopted in any other applications where a reasonable balance between specified design parameters is essential.
The ASIC synthesis enables us to analyze design parameters at a more accurate level. Hence, future work involves standard cell implementation of the proposed FFT processor architecture.

References