International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Fast Moving Vehicle Number Plate Detection

Mr C Vikas
PG Student, M.Tech [TCN], SRM University, Chennai, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The detection of fast moving vehicle is an important part in Intelligent Transportation System.This paper presents a new method for detecting vehicles, which violate rules in real time traffic scenario. The main Process done in three steps: Moving vehicle detection, Number plate detection and Blur Removal. Firstly, Capture the fast moving vehicle by using novel algorithm, which convert video into image frames. Then Number plate extraction of vehicle by using several geometrical features. Finallyremoving the blur from the vehicle number plate by using blind image DE convolution. Experiment results show that this method can improve the efficiency of the moving vehicles number plate detection without blur greatly.

Keywords
Vehicle detection, Number plate Detection, Noise Removing

INTRODUCTION
With the rapid development of highway and the wide use of vehicle, researchers start to pay more attention on the efficient and accurate intelligent transportation systems (ITS). It is widely used for detecting car’s speed, security control in restricted areas, highway surveillance and electric toll collection [1]. Vehicle license plate (VLP) recognition is one of the most important requirements of an ITS. Although any ITS and specifically any VLP recognition contains two part in general, license plate detection and recognition, detecting and segmenting VLP correctly is most important because of existing conditions such as poor illumination, vehicle motion, view- point and distance changes. The problem of automatic VLP recognition has been studied since 1990s. The first approach was based on characteristics of boundaries [2,3]. In this method, an image was binarized and then processed by certain algorithms, such as Hough trans- form, to detect lines. In general, the most common approaches for VLP detection include texture [1,4], color feature [5], edge extraction [6], combining edge and color[7], morphological operation [5,8] and learning-based method [9]. Using color feature is benefit when lighten- ing is unchanged and stable. However methods based on edge and texture are nearly invariant to different illumination and so they are widely used for VLP detection. These methods use the fact that there are many characters in the license plate, so the area contains rich edge and texture information. Zhang et al. [9] proposed learning based method using AdaBoost for VLP detection. They used both global (statistical) and local (Haar-like) features to detect the license plate.
In this paper, we do pre processing for image enhancement at first. The some regions are candidate as a license plate during three procedures. Finallyconsidering geometrical features, the license plate is segmented nearly independent of image capturing conditions.
This paper is organized as follows: in Section 2. We express how our image bank is provided. In Section 3, the proposed algorithm is described and in Section 4 the experimental results are reported. Finally, in Section 5 we have conclusion.

PROVIDED IMAGE BANK
As respects, the aim of this paper is detecting the license plates in images with complex scenes. Due to the unavailability of required images, in several stages by using 2 digital cameras and mobile cameras, we have provided 350 images under various illumination (lightening), different distances and angles of stationary and moving vehicles. After providing images, in order to increase the processing speed and facilitate the license plate detection, input color image is converted to gray scale image. The size of images is 640×480 pixels.

EFFICIENT LICENSE PLATE DETECTION
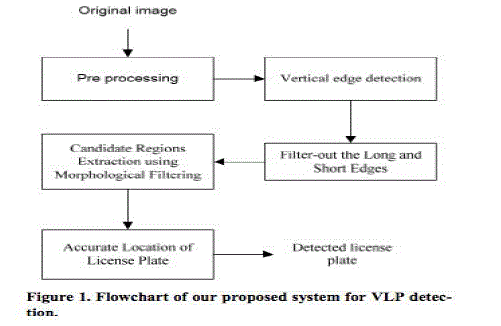
Our, proposed method is composed of several parts, Figure1 shows the flowchart

A.Pre Processing
Low contrast may have the most important effect on failing a license plate detection algorithm. Severe lightening conditions, changing plate orientation and various distances are main reasons for having low contrast and quality in the car images. Therefore, contrast enhancement seems to be necessary, specially at locations where might be a license plate. So, in following we improve different images using two methods, they are intensity variance [6] and edge density [7], and choose the best for pre processing images.
Zheng et al. [6] used the local variance of pixel intensi- ties to improve image contrast at regions that may be plate. They proposed an enhancement function whichincreases image contrast at regions that local variance of intensity is around 20. The enhancement function was suggested as follows:
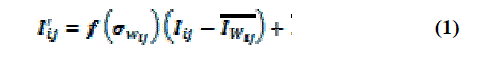image
image
image
Where , and denote the intensities of the pixel inthe input grayscale image and enhanced image, and is a window centered on pixels of grayscale image. and Are average luminance and standard deviation respectively. The enhanced coefficient is defined as follows:
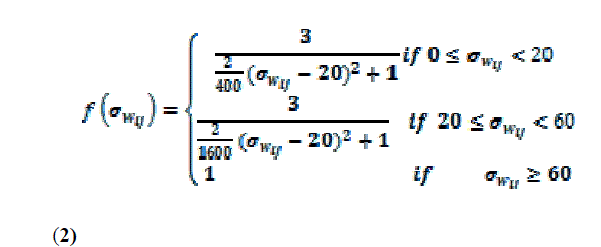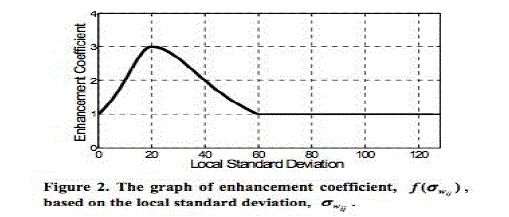
image
With respect to Figure 2, the intensities of pixels in the input grayscale images with local variance between 0 and 60 are enhanced.

C. Edge Density
Abolghasemi et al. [7] used the density of vertical edges (instead of the variance of intensity) as criterion for local enhancement of car image. License plate of the car con- sist of several characters (8 characters for Iranian VLP), so the license plate area contains rich edge information. We can employ the edge information to find the location of plate in an image. At first, they [7] used the vertical sobel mask and obtained the gradient image.

B.Intensity Variance
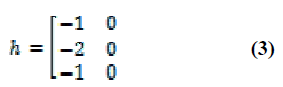image
Then, they compared pixel values with a predefined threshold and the vertical edge image has been achieved.In the next step, the vertical edge image is convolved with the 2-D Gaussian kernel and estimation of the edge density is yielded. The results on a sample image are shown in Figure 4.
In order to enhance the input image with respect to the estimations of edge density, an enhancement coefficient is suggested as follows:
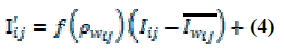image
where , And are explained in the previous step. f(p1) is the weighting function, regarding theestimation of edge density. This function is sketched in Figure 4.
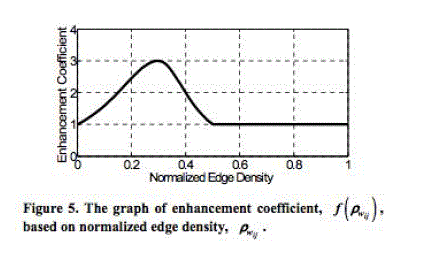
As can be seen in Figure 5, the intensity of pixels with the edge density among 0.15 to 0.45 is to be enhanced. The enhancement coefficient f(p1) is defined as follows:
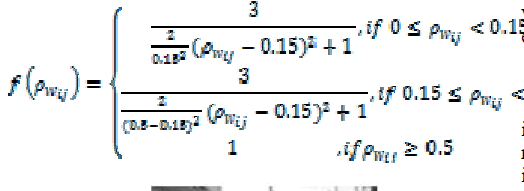image
image
image

DETECTING THE VLP
After enhancing an input image by using suitable method (edge density), we should detect any existed license plate in the improved image. We do the following stages for this purpose.

A.Vertical Edge Detection
Edge detection is one of the most important processes in image analysis. An edge represents the boundary of an object which can be used to identify the shapes and area of the particular object. When there is contrast difference between the object and the background, after applying edge detection, the object edges will be illustrated. We select the vertical sobel operator, Equation (3), to detect the vertical edges.

B.Filter-Out the Long and Short Edges
After extracting vertical edges from the enhanced image, using morphological filtering obtains candidate regions those may be a license plate. But, as it can be seen in Figure 6(a), there are many long background and short noise edges that may interference in the morphological filtering process. In order to resolve this problem, an effective algorithm is used to remove the background andnoise edges [6]. The filter-out image after removing unwanted edges is shown in the Figure 6(b).
image

C. Candidate Regions Extraction Using

Morphological Filtering
Morphological filtering is used as a tool for extracting image components and so representing and describing region shapes such as boundaries. In this part, we use a morphological operation for extracting candidate regions. Hence, we implement the morphological closing and opening that defined as follows:
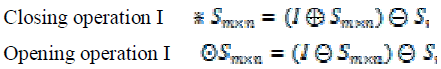image
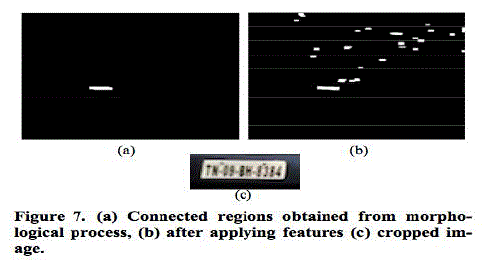
Where and denote dilation and erosion operations, respectively. S1 denote a structuring element with size m all entries in S1 are one. The output of this stage is shown in Figure 7(a).
image

D. Accurate Location of License Plate
After using morphological filtering, still many regionsre candidating as a license plate. So we consider some features such as area, aspect ratio (height per width) and edge density in order to discard wrong candidate regions. Values for these features are set experimentally based on our test images. These features are scale-, luminance- and rotationvariant. Progressive of using these features to remove nonplate candidate regions can be seen in Figure 7(b).

DE-BLURRING THE NUMBER PLATE
First, the blur kernel is estimated from the input image. Then Estimation process is performed in a coarse-tofine fashion in order avoids local minima. Second, using the estimated kernel we apply a standard Deconvolution algorithm estimate latent image.The user supplies four inputs to the algorithm: blurred image B, a rectangular patch within the blurred image, a upper bound on the size of the blur kernel (in pixels), after an initial guess as to orientation of the blur kernel. Additionally, require input image B to have been converted to a linear color - space before processing. In our experiments, applied inverse gamma correction1 with γ= 2.2. In order to estimate the expected blur kernel, we combine all the color channel of the original image within the user specified patch to produce a grayscale blurred patch P.

A.Estimating the blur kernel
Given the a grayscale blurred patch P, we estimate K and then latent patch image finding values with highest probability, guided by prior on the statistics of L. Since these statistics are based on a image gradients rather than the intensities, perform the optimization in the gradient domain, using and the gradients of and P. Because convolution is linear operation, then patch gradients should be equal to the convolution the latent gradients and the kernel: = K, plus noise. We assume that this noise is the Gaussian with variance .As we discussed in the previous section, the prior P( on alatent image gradients is mixture of C zero-mean Gaussians. We use a scarcity prior P(K) for the kernel that encourage zero values in the kernel, and requires all entries to be positive. Specifically, the prior on kernel values is a mixture of D there exponential distributions.Given the measured image gradients , we can write the posterior distribution over the unknowns with Bayes’ Rule:
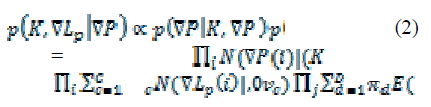image
Where I indicates over image pixels andjindicates over blur kernel elements. So N and E denote Gaussian and Exponential distribution respectively. For tractability, we assume gradients in are independent of each other, as are the elements in and K.

B.Image Reconstruction
The multi-scale inference procedure outputs an estimate of the blur kernel K, marginalized a over all possible reconstructions. To recover the de-blurred image given this estimate the kernel, we experimented with a variety of non-blind, de-convolution methods, including those of Geman [1992], Neelamani [2004] and van Cittert [Zarowin 1994]. While many of these methods perform wellsynthetic test examples, our real image exhibits a range of non- linearities not present in synthetic cases, such as non-Gaussian noise, saturated pixels, residual nonlinearities in tonescale and estimation errors in the kernel. Disappointingly, when run our images, most methods produced an unacceptable level of artifacts.We also used our variation inference scheme on the gradients of the whole image ∇B, while holding K fixed The intensity of image then formed via Poisson reconstruction [Weiss 2001]. Aside from being slow, the inability to model the non-linearities mentioned above resulted in reconstructions no better than other approaches.
As L typically is large, speed considerations a simple methods attractive. Consequently, we reconstruct the latent color image L with the Richardson-Lucy (RL) algorithm [Richardson1972; Lucy 1974]. While the RL performed comparably to the other methods evaluated, it has the advantage of taking only a few minutes, even on large images (other, more complex methods, took hours or days). RL is non-blind de-convolution algorithm that iteratively maximizes the likelihood function of a Poisson statistics image noise model. One benefit this over more direct methods is that it gives only non-negative output values. We use Mat lab’s implementation of the algorithm to estimate L, given K, treating each color channel independently Used10RL iterations, although for alarge blur kernels, more will needed. Before running RL, we can clean up K by applying a dynamic threshold, based on the maximum intensity values within the kernel, which sets all elements below an certain value to zero, so reducing the kernel noise. The output of RL was by gamma corrected using γ = 2.2 and its intensity histogram matched to that of B (using Matlab’s histeq function), resulting in L.

5. Expermient Results
To detect the effect of the proposed algorithm, we use the following traffic video image sequences, with the size of 320*240, for testing. Fig.8 shows the detection results.
image
image

CONCLUSION
In this paper, we have presented a new and fast vehicle detecting system capable of robustly working under most circumstances. The system is general enough to be capable of detecting and classifying vehicles while requiring only minimal scene-specific parameters, which can be obtained through training. The exact detection of the vehicle number plate in different scenarios makes the key part.

References