Keywords
|
| Hydro-thermal scheduling, Genetic Algorithm, Differential Evolution, MATLAB. |
INTRODUCTION
|
| Short-term hydrothermal scheduling is a crucial task in the economic operation of a power system. A good generation schedule reduces the production cost, increases the system reliability, and maximizes the energy capability of reservoirs by utilizing the limited water resource as in[9]. The primary objective of the short term hydro thermal scheduling is to find the optimal amount of generated powers for hydro and thermal units so as to minimize the fuel cost of thermal units. The problem requires that a given amount of water be used in such a way so as to achieve this objective, which is usually much more complex than the scheduling of all thermal system.The short range problem usually has an optimization interval of a day or a week. This period is normally divided into sub-intervals for scheduled purposes. Here the load, water inflows and unit availability are assumed to be known. A set of starting conditions being given, an optimal hourly schedule can be prepared that minimizes a desired objective while meeting system constraints successfully. Cost optimization of hydro stations can be achieved by assuming the water head constant and converting the incremental water rate characteristics to incremental fuel cost curve by multiplying it with the cost of water per cubic meter and applying the conventional technique of minimizing the cost function. |
| Genetic algorithm (GA)are computational search techniques based on models of genetic change in a population of individuals bearing a close resemblance with the science of evolution and genetics. These models consist of three basic elements: |
| • Fitness which governs the individual’s ability to influence future generations. |
| • Reproduction operation which produces offspring for the next generation, through a selection and mating process. |
| • Geneticoperatorswhich determine the genetic makeupof the offspring. |
| DE or differential evolution belongs to the class of evolutionary algorithms that include evolution strategies (ES) and conventional genetic algorithms (GA) as in[6], DE differs from the conventional genetic algorithms in its use of perturbing vectors, which are the difference between two randomly chosen vectors. DE is a scheme which it generates the trial vectors from a set of initial populations. In each step, DE mutates vectors by adding weighted random vectors differentials to them. If the fitness of the trial vector is better than that of the target vector, the trial vector replaces the target vector in the next generation. DE offers several strategies for optimization. They are classified according to the following notations such as DE/x/y/z, where x refers to the method used for generating parent vector that will form the base for mutated vector, y indicates the number of difference vector used in mutation process and z is the crossover scheme used in the cross over operation to create the offspring population. The symbol x can be ‘rand’ (randomly chosen vector) or ‘best’ (the best vector found so far). The symbol y i.e. the number of difference vector, is normally set to be 1 or 2. For cross over operation, a binomial (notation: ‘bin’) or exponential (notation: ‘exp’) operation is used. The version used here is the DE/rand/1/bin, which is described by the followingsteps:Initializaion, Mutation operation, cross over operation. |
LITERATURE SURVEY
|
| Hydrothermal scheduling is required in order to find the optimum allocation of hydro energy so that the annual operating cost of a mixed hydrothermal system is minimized. Over the last decade the hydrothermal scheduling problem has been the subject of considerable discussion in the power literature DeepikaYadav, R. Naresh and V. Sharma gave solution of hydro thermal scheduling using real time variable genetic algorithm as in[10] The available methods differ in the system modelling assumptions and the solution. The annual hydrothermal scheduling problem involves the minimization of the annual operating cost of a power system subject to the several equality and inequality constraints imposed by the physical laws governing the system and by the equipment ratings. Different methods have been proposed for the solution of these problems in the past. Methods based on Lagrangian multiplier and gradient search techniques as in [9] for finding the most economical hydrothermal generation schedule under practical constraints have been well documented. Houzhong Yan as in [5] utilized calculus of variation for short range scheduling problem and proposed the well known coordination equations.In this respect stochastic search algorithms like simulated annealing (SA) , genetic algorithm (GA) [11], evolutionary strategy (ES) [6] and evolutionary programming (EP) may prove to be very efficient in solving highly nonlinear HS problems since they do not place any restriction on the shape of the cost curves and other non-linearities in model representation. Although these heuristic methods do not always guarantee the globally optimal solution, they will provide a reasonable solution (suboptimal near globally optimal) in a short CPU time. |
SYSTEM MODEL AND ASSUMPTIONS
|
| In this paper algorithm for both Genetic Algorithm and Differential Evolution methods are used for finding which method is more economical and thus cost is determined. The system model considered here consists of one thermal power plant and one hydro power plant. The comparative study of the results is done further. |
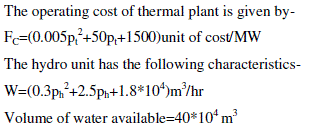 |
| The schedule of the load is as specified |
| 12 mid-night-12noon: 500 MW, 12noon-12midnight:900 MW |
| Consider €1=0.001, €2=0.001, |
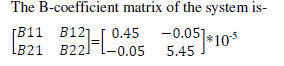 |
| Assumptions made are- |
| 1.Water head of the reservoir is assumed constant during operation |
| 2.Water spillage from the water reservoir has been neglected |
| 3.The operating schedule is for 24 hours and each interval is for one hour |
| 4.The beginning and ending water storage volumes are specified |
| 5.Load demand equality constraints Pik=Pdk +Plossk |
ALGORITHM OF THE METHODS
|
| GENETIC ALGORITHM |
| 1. Read data, namely cost coefficients, ai, bi, ci, B-coefficients, B(i=1,2,3,….,NG; j=1,2,3,……NG),number of steps for gamma correction (d), number of generations(z),step size α, water availability throughout all intervals q, l length of string, L population size, pc crossover probability, pm mutation probability, number of intervals (t), λmin and λmax for each intervals etc. |
| 2. Generate an array of random numbers. Generate the population λj (j=1, 2,…..L) by flipping the coin for both intervals. The bit is set according to the coin flip as bij =1 if p=1 or 0<=p otherwise bij=0 where p=0.5. |
| 3. Generate the initial population of gamma. |
| 4. If number of iterations for gamma correction>= d then GOTO step 24 else repeat step 4 to 23. |
| 5. If number of intervals <= t repeat step 6 to 20 for each interval and increment interval counter each time else GOTO step 4. |
| 6. Set the generation counter k=0, fmax=0 and fmin=1. |
| 7. If k>=z GOTO step5 else repeat step 7 to 20 |
| 8. Increment generation counter k=k+1and set population counter j=0. |
| 9.Increment population counter j=j+1 |
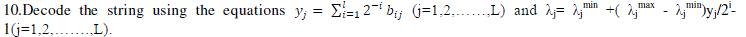 |
| 11. Use Gauss Elimination method to find Pi j (i=1,2,……NG including hydel and thermal generators). |
| 12. Calculate the transmission loss. |
| 13. Find out εj |
| 14. Find out the fitness values from the fitness function f j=1/(1+α*εj/Pd). If (fj>fmax) then set fmax= fj and if ((fj<fmin) then set fmin= fj |
| 15. If (j<L) then GOTO step 9 and repeat. |
| 16. Find population with maximum fitness and average fitness of the population. |
| 17. Select the parents for crossover using stochastic remainder roulette wheel selection |
| 18. Perform single point crossover for the selected parents. |
| 19. Perform the mutation. |
| 20. Modify and create the new population of lambda for the next generation. |
| 21. Check whether the total available water is enough for hydel generation in each interval. |
| 22. Calculate the error in initially anticipated values of gammas’ population. |
| 23. Modify the values of gamma in gammas’ population and GOTO step 4. |
| 24. Stop. |
| DIFFERENTIAL EVOLUTION |
| 1.The problem variables to be determined are represented as a j-dimensional trial vector, where each vector is an individual of the population to be evolved. |
| 2. An initial population of parent vectors Qk for k=1,2,..Np is selected from a random feasiblerange of in each dimension.The distribution of these parent vectors is uniform. |
| 3.An offspring is generated from each parent with adoption of strategy parameter based on scaled cost. |
| 4.Fitness function is evaluated for each individual of both parent and child populations. |
| 5.A competitor is chosen randomly from combined population of 2 Np trial solution |
| 6. After the competition is over the 2Np trial solutions are sorted according to their cores from highest to lowest. |
| 7.If the current generation is greater than or equal to the maximum generation print the results and sto, otherwise repeat step 3 to 6. |
| 8.If the fitness of the trial vector is better than that of the target vector, the trial vector replaces the target vector in the next generation |
RESULT AND DISCUSSION
|
| Result of Hydrothermal Scheduling using Genetic Algorithm |
| avgpowerhydal1 =95.4213 |
| avgpowerthermal1 = 254.9387 |
| avgpowerhydal2 =110.5212 |
| avgpowerthermal2 =592.1447 |
| averageloss1 =3.2459 |
| averageloss2 =15.7512 |
| rupees1 =3.45212e+003 |
| rupees2 =7.81254e+003 |
| Result of Hydrothermal Scheduling using Differential Evolution |
| avgpowerhydal1 =95.8512 |
| avgpowerthermal1 = 254.7574 |
| avgpowerhydal2 =111.0452 |
| avgpowerthermal2 =591.1283 |
| averageloss1 =3.2339 |
| averageloss2 =15.7212 |
| rupees1 =3.44326e+003 |
| rupees2 =7.79885e+003 |
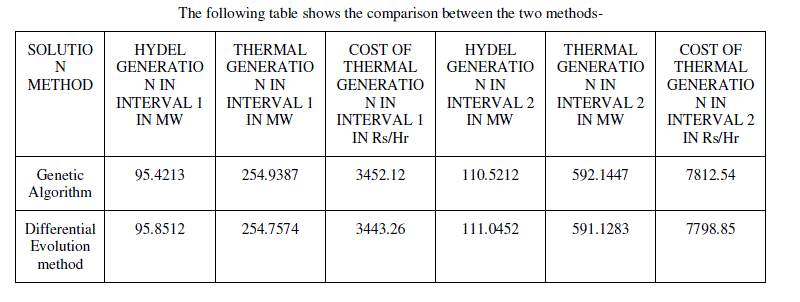 |
| The following table shows Cost of Thermal generation in Rs/hr- |
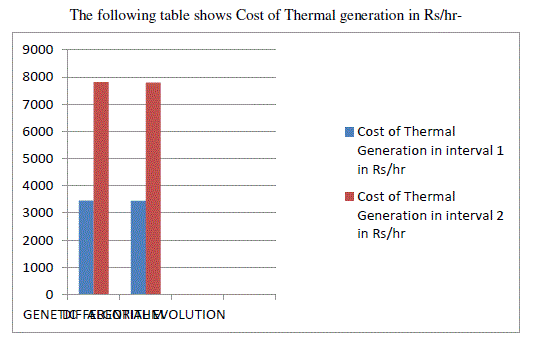 |
| From the results shown above and the comparison between the two methods it is clear that both the methods are able to give the economic cost of generation of the thermal plant but Differential Evolution method is more advantageous as compared to Genetic Algorithm method. Differential evolution method shows more Hydel power generation in each interval as compared to Genetic Algorithm. As the running cost of Hydel plant is low so it is more economical of using Differential Evolution as compared to Genetic Algorithm. |
CONCLUSION
|
| In the concluding remarks it can be stated that the result obtained by Differential Evolutionary Algorithm is the best as compared to the solutions obtained by the Genetic Algorithm. So Fixed Head Short Term Hydrothermal Scheduling considering Transmission Loss can be done by Differential Evolutionary Algorithm in order minimize the generation cost of thermal power plant and by following the constraints also. On doing this program some assumptions were taken into consideration such as water head of hydro reservoir to be constant during operation, water spillage from the water reservoir has been neglected, the operating schedule is for 24 hours while each interval is for one hour, beginning and ending water storage volumes are specified. |
References
|
- Wood A., WollenburgB.,”Power generation Operation and control”,New York:Wiley,1996
- D.P Kothari, J.S Dhillon,”Power system optimization” PHI learning private limited New Delhi 2011
- L.K Kirchmayer, “Economic operation of power systems”,Johnwileyand sons,NewYork,N.Y 1958
- Houzhong Yan, Peter B. LuhXiaohong Guan, Peter m Rogan”Scheduling of hydrothermal power system” IEEE transactions on power system, vol8,no 3, august 1993
- Houzhong Yan, Peter B. LuhXiaohong Guan, Peter m Rogan” Optimization based scheduling of hydrothermal system with pumped storage units” IEEE transactions on power system, vol9,no 2, may 1994
- Rainer Storn,KennethPrice,”Differential evolution–a simple and efficient heuristic for global optimization over continuous space” Journal of global optimizationSpringer,Vol 11, pp341-359,1997
- J. P. S. Catala,y, S. J. P. S. Mariano1, V. M. F. Mendes2 and L. A. F. M.Ferreira3” Nonlinear optimization method for short-term hydro scheduling considering head-dependency” European transactions on electrical power Euro. Trans. Electr. Power (2008)
- J. P. S. Catalão, S. J. P. S. Mariano, V. M. F. Mendes, and L. A. F. M. Ferreira,” Scheduling of Head-Sensitive Cascaded HydroSystems: A Nonlinear Approach”, IEEE transactions on power system,vol 24, No1, 2009
- Rafael N. Rodrigues, Edson L. da Silva,Erlon C. Finardi, and Fabricio Y. K. Takigawa,”Solving the Short-Term Scheduling Problem of Hydrothermal Systems via Lagrangian Relaxation and Augmented Lagrangian” Hindawi Publishing Corporation Mathematical Problems in Engineering Volume 2012, Article ID 856178,18 pages
- DeepikaYadav, R. Naresh and V. Sharma,” Fixed head short term hydrothermal scheduling using real variable genetic algorithm”,Internationaljournal of electrical engineering and technology,vol3,pp430-443,september2012
- M.M. Salama, M.M. Elgazar, S.M. Abdelmaksoud, H.A. Henry,”Short Term Optimal Generation Scheduling of Fixed Head Hydrothermal System Using Genetic Algorithmand Constriction Factor Based Particle Swarm Optimization Technique “,vol3,Issue5,2013
|