ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
A. Appa Rao1, M. Win Babu2 and K.S. Linga Murthy3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Practical rural distribution feeders have failed to converge while using NR and FDLF methods. Therefore, a new load flow technique for radial distribution networks by using node and branch numbering scheme will be developed. In the forward sweep, the voltage at each downstream bus is then updated by the real and imaginary components of the calculated bus voltages. The procedure stops after the mismatch of the calculated and specified Voltages at the substation is less than a convergence tolerance. A Forward sweeping method for solving radial distribution networks will be implemented. Thus, computationally, the proposed method will be a very efficient and requires less computer memory storage as all data is stored in vector form. The load flow will be run in MATLAB for solving the equations.
Keywords |
| load flow analysis, radial distribution systems, forward sweeping, buses, node voltages. |
INTRODUCTION |
| Load Flow Studies are performed on Power Systems to understand the nature of the installed network. This understanding gives the knowledge of the installed Generation Systems, Loads connected, Losses incurred, and also the flexibility of the system to allow future load connections. So, Load Flow or Power Flow analysis is becomes a vital part of any Power System, as without this information, maintaining the network and regulating it within specified limits becomes just a blind control of some wires, in which current flows [4]. Generally distribution systems are radial and the R/X ratio is very high. For this reason distribution systems are ill-condition, and conventional Newton Raphson (NR) and fast decoupled load flow (FDLF) methods [1, 2, 3, and 7] are inefficient in solving such systems. |
| Power flow study provides valuable information for power engineers with ability to quickly simulate the operation of the system. It is becoming apparent that presently working load flow techniques of transmission system are not suitable for distribution system [8]. The main difference is the presence of number of different types of devices, multiphase possibilities and widely varying types of loads in the distribution systems. The distribution power flow involves, first of all, finding all the node voltages. From these voltages, it is possible to compute current directly, power flows, system losses and other steady state quantities .some applications, especially in the fields of optimization of distribution system, and distribution automation (i.e., VAR planning, network optimization, state estimation, etc.), need repeated fast load flow solutions. In these applications it is important that the load flow problem is solved as efficiently as possible. |
| In this paper a forward sweeping method is proposed to solve the radial distribution system. The proposed method is tested by taking 12 and 28 node radial distribution systems. This method develops a new load flow technique for radial distribution systems by using node and branch numbering scheme. The forward sweeping method solves a recursive relation of voltage magnitudes. The load flow will be run in MATLAB for solving the equations. The mathematical formulation of the proposed load flow method is described in the following section. |
PROBLEM FORMULATION |
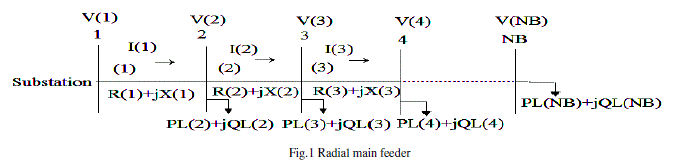
| The load flow of a single source network can be solved iteratively from two sets of recursive equations in forward propagation. These recursive equations are derived as follows. Fig. 1 shows radial main feeder only. The one line diagram has n nodes and n-1 branches. Fig. 2 shows the representation of 2 nodes in a distribution line. |
 |
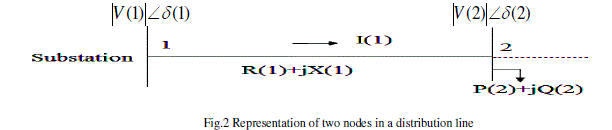 |
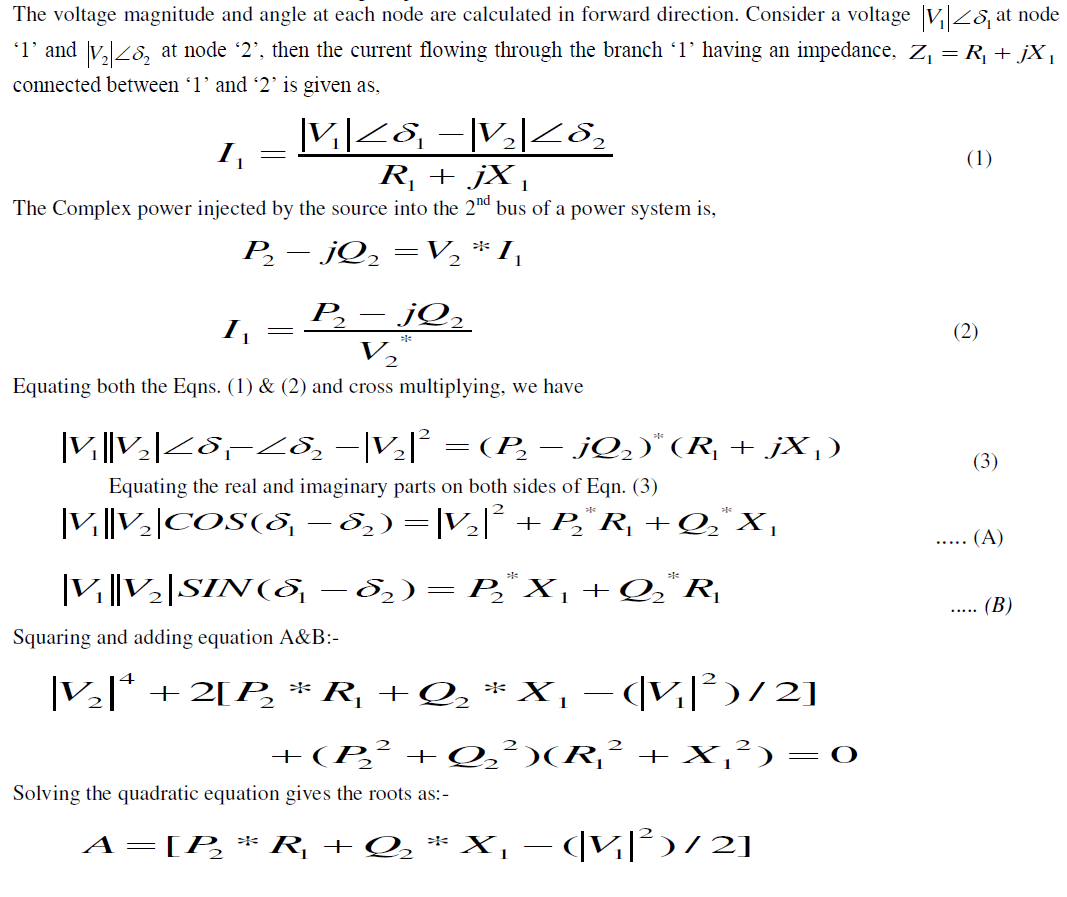 |
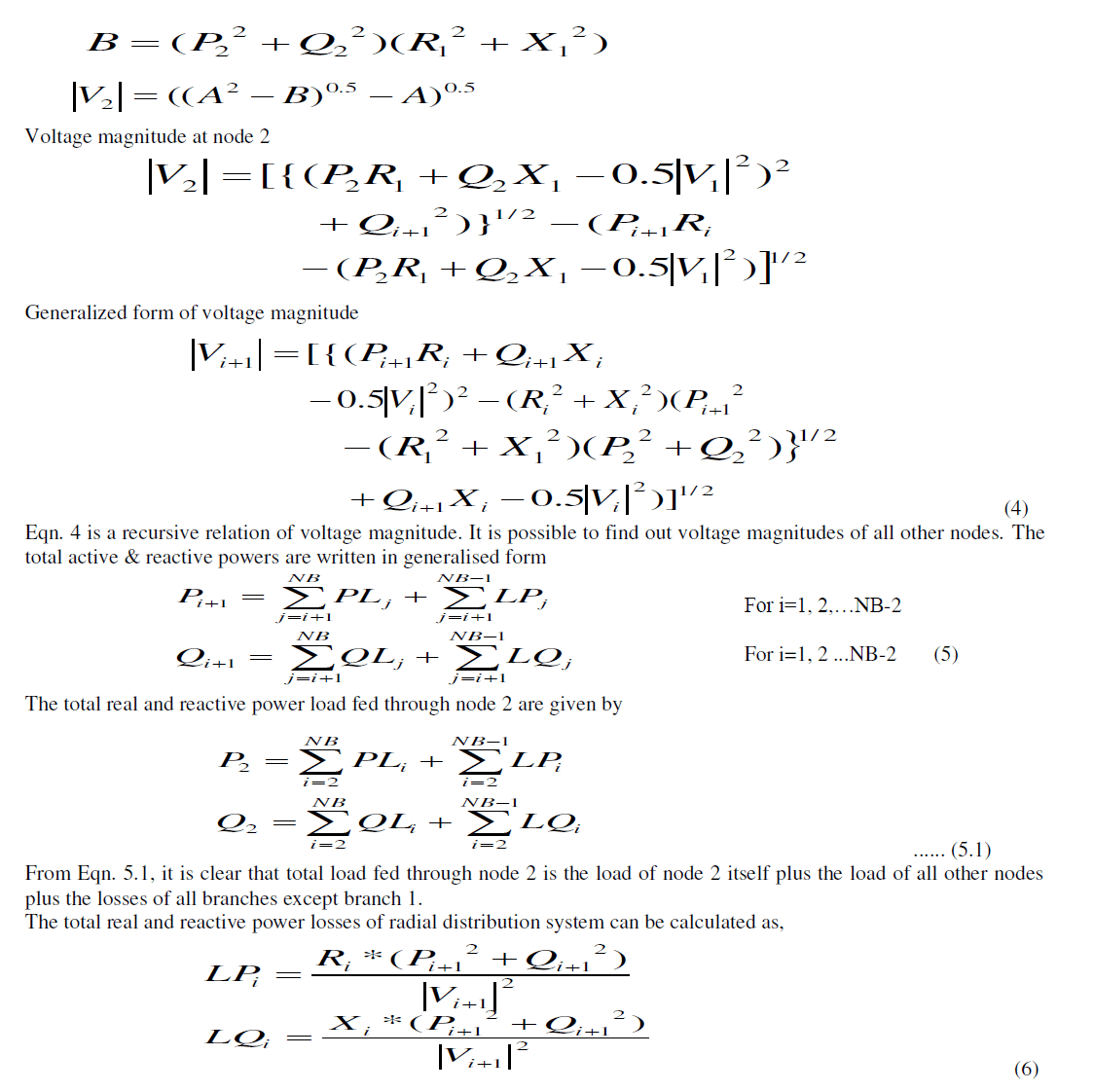 |
POWER FLOW CALCULATION |
| Initially assuming a flat voltage profile i.e., setting the voltage equal to 1.0 Pu at every node, the flow chart for load flow is shown in Fig. 3. The updated effective power flows in each branch are obtained using Eqns. (5) by considering the node voltages of previous iteration. The purpose of the forward sweeping is to calculate the voltages at each node and their angles using Eqns. (4) starting from the feeder source node. |
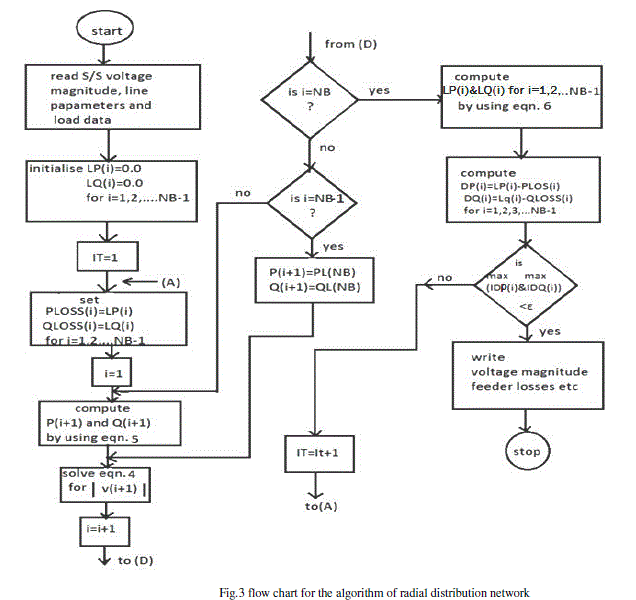 |
The load flow algorithm is as follows: |
 |
 |
RESULTS |
| A. Example 1 |
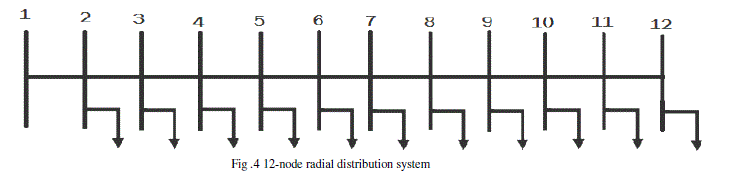
| The line and load data of 12-node, 12.66 KV radial distribution system shown in fig. 4 is taken from [4], Substation |
 |
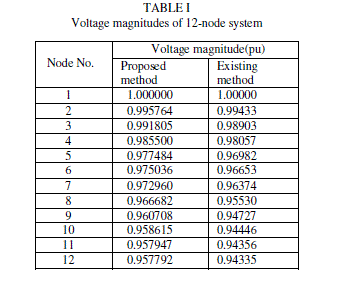 |
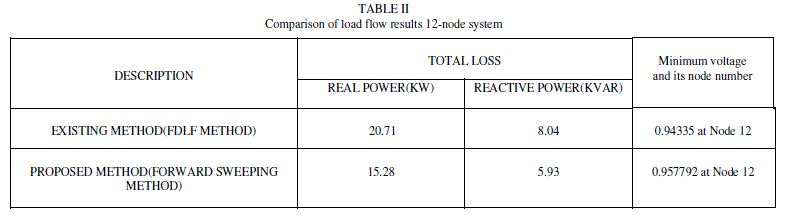
| The total real and reactive power losses of the system are 15.28 KW and 5.93 KVAR respectively. These are 26.21% and 26.24% of their total loads. The minimum voltage of the system is 0.957792 p.u.at node 12. Comparison of load flow results of the proposed method and the existing method [2] is given in table II. |
 |
| B. Example 2 |
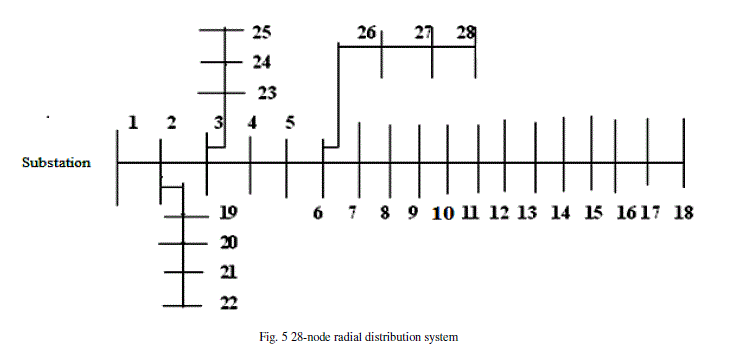
| The line and load data of 28-node, 12.66KV radial distribution system shown in fig.5 is taken from [4], |
 |
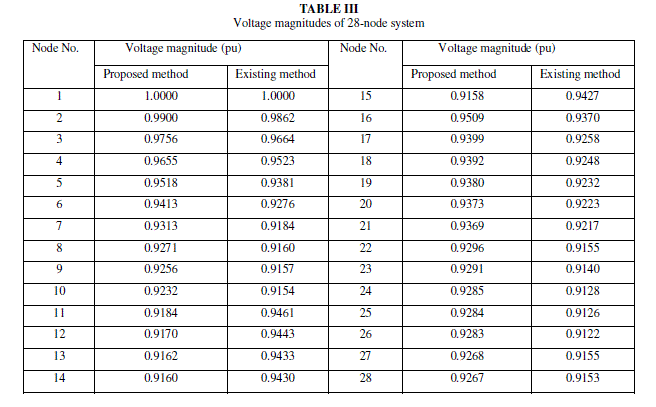 |
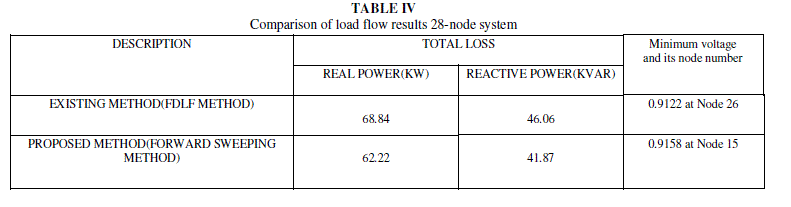
| The total real and reactive power losses of the system are 62.22 KW and 41.87 KVAR respectively. These are 9.62% and 9.10% of their total loads. The minimum voltage of the system is 0.9158 p.u.at node 15. Comparison of load flow results of the proposed method and the existing method [2] is given in table IV. |
 |
CONCLUSION |
| The forward sweeping method guarantees the convergence of any practical radial distribution networks with realistic R/X ratio. The forward sweeping method is practically more efficient with respect to the voltage magnitudes and real and reactive power losses. From the results 12-node system can be observed that without any change in the voltage profile the real power losses are reduced by 26.21% and reactive power losses are reduced by 26.24% and 28- node system can be observed that without any change in the voltage profile the real power losses are reduced by 9.62% and reactive power losses are reduced by 9.10%. |
References |
|